Matematické Fórum

Než použít rovnici ve tvaru co jsi zmínil, [mathjax]y\frac{\mathrm{d} y}{\mathrm{d}t }^{2}=ly[/mathjax] tedy [mathjax]y\frac{\mathrm{d} y}{\mathrm{d}t }^{2}-ly=0[/mathjax] je lepší psát rovnici ve tvaru [mathjax]y\frac{\mathrm{d} y}{\mathrm{d}t }^{2}+ly=0[/mathjax] nebo rovnou [mathjax]y\frac{\mathrm{d} y}{\mathrm{d}t }^{2}+ \omega^2 y=0[/mathjax].

Protože abychom dostali rovnici harmonického kmitání, musí tam být všude stejná znaménka (a přirozené je aby tam byla kladná). Pokud tam bude jedno plus a jedno minus, vede to na řešení dvou reálných exponenciál, a jedna z nich je "nestabilní", tj s rostoucím časem utíká k nekonečnu. Což rozhodně není harmonický oscilátor, a ani žádný jiný pasivní či konzervativní systém.


Jinak tvé otázce moc nerozumím. Protože odvozovat harmonické kmitání z kruhového pohybu se dělá dokud člověk nezná diferenciální rovnice. Potom už je to zbytečné, a v podstatě starost navíc. Takže moc nevím, co tě vlastně trápí, jestli to, jak se řeší ta rovnice harmonického kmitání (jak se z toho odvodí ten sinus), nebo to, jak to souvisí s rotačním pohybem.

Pokud jde o ta řešení...trik je v tom, že tam musí vyjít ta odmocnina ze záporného čísla, tedy [mathjax]\sqrt{-\omega^2} = \pm i \omega[/mathjax]. A součet dvou takovýchto exponenciál dává cosinus, rozdíl sinus, viz tady

Mějme konzervativní silové pole (například pole elektrostatických sil), ve kterém se pohybuje náboj.
V takovém poli neprobíhá disipace mechanické energie náboje na vnitřní energii (na náboj působí pouze elektrostatická síla). První termodynamický zákon pro tento náboj je tedy ve tvaru:

Z toho mi vyplývá, že práce v této rovnici nemůže být definována pro působení elektrostatické síly (potom vychází ).

Práce v prvním TDZ tedy není definována pro konzervativní silová pole?

Ahoj,

OiBobik napsal(a):

↑↑ check_drummer:

Jinak k tomu počítání vesmíru - asi je potřeba ještě poněkud více zpřesnit, co se myslí tím počítačem a simulací - ona to ve své podstatě je zase nějaká fyzická krabice, ve které sem a tam lítaj nějaké elektrony. Takže když si to tak člověk vezme, on ten vesmír samotný je takový docela dobrý počítač, který se simuluje (a la "nejpřesnější mapa území je nakonec ono území samotné").

Ono je to vcelku jedno, jak to budeme simulovat - řekněme, že to zařízení bude na principu dnešního počítače (tj. paměť, jedničky a nuly) - pak by ovšem bylo asi dost obtížné npř. zjistit, co znamená, že se "subjekt svobodně rozhodl" nebo "subjekt pocítil bolest", apod. - ale možné by to šlo pomocí nějakých vhodných funkcí zkoumaného stavu.

OiBobik napsal(a):

Pokud se vezme nějaký konzervativnější model počítače, tak tam se člověk zase dostane do jiných nesnází, typu reprezentace reálných čísel

Možná, že stačí počítat jen s racionálními čísly s dostatečnou přesností - vždyť přece máme nějaké meze pozorování (Planckova délka a planckův čas - pozn: není tohle např. indikátor toho, že nás někdo simuluje (aproximuje)? :-)), tak možná nakonec půjde vše popsat pomocí zlomků s dost velkými - ale omezenými jmenovateli. No a pokud ne, tak budeme vše aproximovat zlomky, ale bude to pomalejší a méně přesné, ale půjde to. Ostatně, dostatečně přesná aproximace by také stačila. Pak je tu ještě otázka, zda se v přírodě reálná čísla vůbec vyskytují, resp. zda je nutné je uvažovat. Kde se např. ve vesmíru vyskytuje 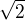? :-) A odpovíš-li, že v úhlopříčce čtverece, pak se ptám, kde se ve vesmíru vyskytuje čtverec? :-)

OiBobik napsal(a):

Ale nechme toho, spíš se podívejme, co s tou real-life aplikací simulace: Představme si, že Pepík chce vědět, co si má dát k snídani. Tak to nabuší do mašiny....
...Mimochodem, přijde mi, že buď se ta věc nezastaví, nebo všechny levely simulace ukážou něco jako 'Pepík si dal banán. Pepík byl šťastný.' "Já chci být taky šťasný!" řekl si Metapepík. A dal si banán. A byl šťastný. (a jakmile to viděl MetaMetapepík, řek si "Já chci být taky šťasný!" A dal si banán. A byl šťastný. ...)

Možná by kadžý level simulace zvolil jinou aproximaci reality a výsledky by nebyly stejné... na druhou stranu spustit další level simulace by byl již dost netriviální akt - simulovaný subjekt by musel "objevit", jak lze takovou simulaci provést - a musel by se "rozhodnout" (např. projevem svobodné vůle :-) tuto simulaci opravdu provést. Ale opravdu bych nechtěl takový stav interpretovat - např. zkoumat co se stalo v sedmé úrovni vnoření - kdo ví, jestli by vůbec bylo snadné tuto interpretaci provést i v první úrovni - to je něco jako strojový kód - dělá to zajímavé věci, ale díky kódu tvaru "rozsypaný čaj" není jeho interpretace ("disasembling") snadná...

Ahoj,kdo poradí jak na to?

Výrobce dostal objednávku na výrobu konzerv tvaru válce. Jaký má být rozměr válce,aby bylo použito co nejméně materiálu? Objem válce je 250 ml.

ahoj mám problém s tímto příkladem, nevim jak začít.

Určete rozměry plechové konzervy tvaru rotačního válce daného objemu 1 litr, abychom na výrobu spotřebovali co nejméně plechu.


díky