Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematických struktur
- » IMC 2009, den 2, úloha 4 (TOTO TÉMA JE VYŘEŠENÉ)
#1 01. 08. 2009 00:49
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4247
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
IMC 2009, den 2, úloha 4
Vrátil jsem se z Maďarska a k všeobecnému rozveselení posílám pěknou algebraickou úlohu, kterou jsem tam řešil.
Nechť p>3 je prvočíslo a W je nejmenší množina polynomů nad 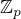 taková, že
taková, že
* obsahuje polynomy  a
a 
* pokud  a
a  pak i
pak i 
Najděte velikost množiny W.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#3 03. 08. 2009 00:46
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4247
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: IMC 2009, den 2, úloha 4
↑ lukaszh:Díky ;o)
Ta úloha je fakt pěkná a není tak těžká, jak vypadá.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#4 03. 08. 2009 16:08 — Editoval musixx (18. 08. 2009 10:08)
Re: IMC 2009, den 2, úloha 4
Offline
#5 07. 09. 2009 22:32
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4247
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: IMC 2009, den 2, úloha 4
↑ musixx:Tvé řešení jsem si přečetl až teď, je prakticky shodné s mým. Možnost p=3 je IMHO vyloučena proto, že je polynom zadán ne formálně sumou, ale pomocí tří teček, vyloučením p=3 dosáhneme naprosté jednoznačnosti zadání.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematických struktur
- » IMC 2009, den 2, úloha 4 (TOTO TÉMA JE VYŘEŠENÉ)

 ?
? a
a  .
. , a protože
, a protože 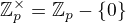 pro prvočíslo
pro prvočíslo  , tak je jasné, že b(x) je identita vyjma jedničky a nuly, jejichž funkční hodnoty jsou prohozené. EDIT: Poslední součin je nula pro všechna x různá od 0 a 1 a je snadné se podívat, kolik je b(0) a b(1).
, tak je jasné, že b(x) je identita vyjma jedničky a nuly, jejichž funkční hodnoty jsou prohozené. EDIT: Poslední součin je nula pro všechna x různá od 0 a 1 a je snadné se podívat, kolik je b(0) a b(1). a
a  tedy dají polynom
tedy dají polynom  , jehož funkční hodnoty jsou permutace z (0,1,2,...,p-1) - máme totiž k dispozici operaci transpozice prvních dvou prvků (
, jehož funkční hodnoty jsou permutace z (0,1,2,...,p-1) - máme totiž k dispozici operaci transpozice prvních dvou prvků ( se toto pomocné tvrzení o funkčních hodnotách neztratí, protože je
se toto pomocné tvrzení o funkčních hodnotách neztratí, protože je 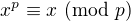 .
.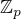 nenulový pro p prvočíslo, tedy existuje v
nenulový pro p prvočíslo, tedy existuje v ![kopírovat do textarea ${\mathbb Z}_p[x]$](/mathtex/c9/c916b6cc7658772668d00bfe4ea18d99.gif) jediný polynom (Langrangeův interpolační), který má p předepsaných funkčních hodnot a je stupně nejvýše p-1.
jediný polynom (Langrangeův interpolační), který má p předepsaných funkčních hodnot a je stupně nejvýše p-1.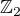 , resp. z toho jen náznakem zadaného tvaru není ani úplně jasné, jak b(x) pro p=2 vypadá).
, resp. z toho jen náznakem zadaného tvaru není ani úplně jasné, jak b(x) pro p=2 vypadá).