Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 17. 08. 2018 05:56 — Editoval vanok (17. 08. 2018 06:56)
Re: Transformační matice
Ahoj ↑ 1jirka22:,
Tvoja matica je matica rotacii okolo osy  uhlu
uhlu  .
.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 17. 08. 2018 12:24 — Editoval vanok (17. 08. 2018 13:14)
Re: Transformační matice
↑ 1jirka22:,
Pripomeniem, ti to co ste iste videli v skole ( ale si mozno samouk a si si to este neuvodemil). Tvoja matica popisuje ( v euklidovskom priestore) ako sa tranformuje ortonornormalna baza priamotocivej orientacii rotaciu okolo osy  uhlom ( v tvojom pripade)
uhlom ( v tvojom pripade)  .
.
Obraz vektoru  je ..,,
je ..,,
A ako mozes konstatovat obraz je zasa ortonormalna baza ...
Na webe najdes o tom vela informacii ( hladaj aj v inych jazykoch, napr po angl. ).
Poznamka. Ak uvazujes v priestore nejaku rotaciu, tak mozes nast ortornormalnu bazu v ktorej sa ocitnes v podobnej situzcii ako v tej co si popisal.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#5 17. 08. 2018 15:31
Re: Transformační matice
Nejlepší je asi vzpomenout, jak je vlastně sinus a cosinus definovaný.
Pokud máme vektor, jež míří ve směru osy x a má délku L, a otočíme jej o úhel  , budou nové souřadnice tohoto vektoru
, budou nové souřadnice tohoto vektoru 

a protože to L je v našem případě také x-ová složka, protože míří ve směru osy x (takže y-ová složka je rovna nule), můžeme rovnou psát

Stejně tak pro vektor jež míří jen do osy y, můžeme udělat to samé

a stejně tak jako předtím bylo L x-ová složka, tak teď je y-ová

Pokud vektor míří do obecného směru, tj. má nenulovou x-ovou i y-ovou složku, můžeme jej vyjádřit jako sučet dvou vektorů, z nichž jeden míří do směru osy x, a druhý do směru osy y.
Takže po sečtení těch našich rovnic dostaneme

Což už je to samé, jako v tom maticovém zápise. No - mám tam naopak znaménko, zřejmě jsem ten úhel uvažoval na druhou stranu, než je to zvykem. Ale v principu je to to samé.
Offline
#6 17. 08. 2018 16:29 — Editoval vanok (19. 08. 2018 10:04)
Re: Transformační matice
Ahoj ↑ MichalAld:,
Ty mas ten uhol spravne vybrany urobil si v rovine (xy) otocenie o uhol  v kladnom ( smere (fyzici by povedali proti hodinovym rucickam).
v kladnom ( smere (fyzici by povedali proti hodinovym rucickam).
A tiez si dobre popisal obraz rotacie dvoch vektorov urcitej ortogonalnej kladne orientovanej bazy roviny. ( I ked sa to popisuje jednoduchsie vdaka vektorom bazy... a to scitanie nie je klasicke)
Ale v priestore mame na viac os z ( kolmu na rovinu (xy) )je vytvorena pevnymi bodmi rotacie.
Mas pravdu, ze je postup riadok po riadku je identicky zapis ako ten maticovy.
Pridam, ze v euklidovskom orientovanom priestore matice rotacii su presne ortogonalne matice ktorych determinant je 1. ( ich vlasnosti sa studuju na zaciatku VS. Aj na technickych smeroch)
Poznamka.
Je uzitocne vediet urcit ci nejaka dana matica typu 3x3 je matica rotacie a urcit jej os a uhol otocenia.
Zajtra pridam jeden konkretny priklad.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#7 18. 08. 2018 12:01 — Editoval vanok (18. 08. 2018 12:14)
Re: Transformační matice
Pridam jeden konkretny priklad matice rotacie, ktory som slubil.
Vysetrite zobrazenie matice

Navod. Ukazte, ze ide o rotaciu ( aka je jej os a uhol?).
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#8 18. 08. 2018 23:34 — Editoval vanok (19. 08. 2018 01:06)
Re: Transformační matice
Trocha podrobnejsi navod.
Ako prve mozme vypocitat 
Potom ukazte, ze

Co z ortogonalitou ukaze, ze skutocne mame rotaciu.
Osa tejto rotacie je vytvorena pevnymi bodmi tohto zobrazenia.
Vieme, ze matica
 je konjugovana z maticou
je konjugovana z maticou 
kde
 je uhol danej rotacie.
je uhol danej rotacie. Znama veta o maticach dve konjugovane matice maju rovnaku stopu
Vyuzite to
Dufam, ze to da myslienku na moznu metodu na riesenie problemov takehoto typu.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#9 19. 08. 2018 10:02 — Editoval vanok (19. 08. 2018 10:07)
Re: Transformační matice
↑ 1jirka22:
A pochopitelne, opacne, je byt schopny napisat maticu rotacie v danej ortonormalnej orientovanej bazy ak pozname jej os a uhol.
Dufam, ze som ti pomohol trochu si uvedomit, vdaka mojim riadkom v tomto vlakne, co je uzitocne vediet a aj prehlbit na tuto temu.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#10 19. 08. 2018 16:09
Re: Transformační matice
↑ vanok:
Nejde to poznat skrze vlastní čísla, že jde o matici rotace ?
Napadlo mě, že kdyby jedno z vlastních čísel bylo rovno jedné, mohla by to být ta osa rotace.
A pro 2D rotaci mi vychází (jestli jsem teda počítal správně, ale celkem to dává smysl) vlastní čísla
Takže pokud je tato úvaha správná, dostali bychom z vlastních čísel i úhel natočení, a osu rotace určenou vlastním vektorem příslušejícím tomu vlastnímu číslu 1.
Je to korektní postup, nebo to takto nejde ?
Offline
#11 20. 08. 2018 22:35 — Editoval vanok (21. 08. 2018 01:35)
Re: Transformační matice
↑ MichalAld:
Pozdravujem,
Myslim si , akoze vlastne hodnoty matice realnej rotacie v dvojnrozmerneho priestoru nema realne
hodnoty.( Az na uhly  a
a  ) Takto student ktory este nepozna ine prietory bude pracovat v realnom priestore. Metodu prace som naznacil vyssie.
) Takto student ktory este nepozna ine prietory bude pracovat v realnom priestore. Metodu prace som naznacil vyssie.
Doplnok.
Mozme dokazat, matica realnej rotacie v 2D je diagonalabilna v  ( jej det je 1)
( jej det je 1) .
.
Tvoja uvaha je spravna.
Opakujem.
Ale akoze ide o o realne rotacie, tak na riesenie sa pouziva len realny ramec. ( pokial, student nema dostatocne znalosti, a nedokaze ich interpretaciu lebo jeden priestor ma dimenziu 2 a druhy 4).
Ak sa napise charakteristicky polynom tak sa to lahko dokaze.
Dakujem, ze sa o to zaujimas.
Poznamka. Rotacie sa daju generalizovat aj do viac rozmernych priestorov. No vsak to sa asi neuci na technickych smeroch.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#12 22. 08. 2018 10:17
Re: Transformační matice
Pozdravujem ↑ MichalAld:,
Toto https://en.m.wikipedia.org/wiki/Quatern … l_rotation
ta bude iste zaujimat.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#13 22. 08. 2018 18:52 — Editoval MichalAld (22. 08. 2018 18:55)
Re: Transformační matice
vanok napsal(a):
Ak sa napise charakteristicky polynom tak sa to lahko dokaze.
Dakujem, ze sa o to zaujimas.
Poznamka. Rotacie sa daju generalizovat aj do viac rozmernych priestorov. No vsak to sa asi neuci na technickych smeroch.
Já jsem právě nevěděl, jestli krom vlastních čísel není potřeba ještě nějaké další podmínky.
My jsme myslím na univerzitě tady ty transformace (rotace atd) nebrali vůbec. Algebru jsem měli jen jeden semestr, a k tomu ještě ten první, polovinu času jsem ani nevěděl, o čem se tam mluví.
Ale vlastní čísla mne zaujala, jednak jsem to hned pochopil, a jednak to byla (je) taková netriviální věc, že by normálního člověka ani nenapadlo, že něco takového existuje. Takže zajímavé.
(narozdíl od standardního příkladu "najděte inverzní matici k .... (5x5), z čehož mě mohlo vždycky potrefit)
Pokud jde o rotace v prostorech vyšší dimenze, tak s tím jsem se setkal až ve fyzice (dávno po škole) - totiž Lorentzova transformace je vlatně taková "rotace" ve 4D prostoru.
Píšu to ovšem s otazníkem, protože on je to vlastně 3D+T prostor, a má takovou speciální metriku - velikost vektoru se tam nerovná  , ale
, ale 
Plnye z toho spousta takových zvláštních věcí (jako že existují vektory s nulovou velikostí, a přitom nejsou nulové), a také třeba to, že při oné "rotaci", při které se zachovává velikost vektoru, nejde o "pohyb po kružnici" ale o "pohyb po hyperbole". S oblibou se to však také nazývá "rotace" - i když ten úhel vychází tuším imaginární, ale občas si někdo dá tu práci, aby to nazval "zobecněná hyperbolická rotace". V transformační matici pak nejsou siny a cosiny, ale jejich hyperbolické ekvivalenty.
Offline
#14 22. 08. 2018 19:19
Re: Transformační matice
Ahoj ↑ MichalAld:,
Prave som otvoril vlakno v didaktike kde chcem tuto temu trochu rozvinut.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline



 \theta =\frac {\pi}3
\theta =\frac {\pi}3  \theta =-\frac {\pi}3
\theta =-\frac {\pi}3  \mod (2\pi)
\mod (2\pi)  \sin \theta
\sin \theta \sin \theta
\sin \theta 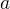 det (\vec n; \vec x; A(\vec x)
det (\vec n; \vec x; A(\vec x) \vec n
\vec n \vec x=\begin {pmatrix} 1 \\0 \\0 \end {pmatrix}
\vec x=\begin {pmatrix} 1 \\0 \\0 \end {pmatrix} Autor skryl část textu. Zobrazit/skrýt!
Autor skryl část textu. Zobrazit/skrýt! \theta =\frac {\pi}3
\theta =\frac {\pi}3