Matematické Fórum

fmfiain · 29. 12. 2018 09:28

Dobrý deň,
v jedných skriptách som našiel výpočet determinantu matice 4x4 tak, že autor najskôr použil Laplaceovu vetu o rozvoji determinantu a tak dostal determinanty matíc 3x3, a tie potom riešil Sarrusovím pravidlom a tak dostal všeobecnú rovnicu nad roviny.

Ja som to po ňom počítal a vychádzalo to. Potom som skúsil iný postup. Urobil som Laplaceovu vetu o rozvoji determinantu na determinant matice 4x4 a potom aj na 3x3, čím som dostal determinanty matíc 2x2. Na to som potom použil výpočet pre maticu druhého rádu.

V oboch prípadoch som dostal rôzne rovnice nad roviny.

Môžete mi poradiť, či sú oba postupy správne.

Ďakujem.

jarrro · 29. 12. 2018 09:39

determinant musí vychádzať rovnako každým postupom

fmfiain · 29. 12. 2018 10:03

↑ jarrro:
Dobrý deň,
skúste vypočítať tento determinant Sarrusovým pravidlom a potom tou druhou možnostou.

Tu je matica: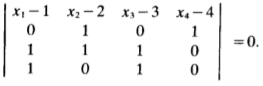

//forum.matweb.cz/upload3/img/2018-12/74021_2.png

a tu je výsledok Sarrusovým pravidlom:

Skúste tú maticu vypočítať tou druhou metódou.

Stýv · 29. 12. 2018 10:42

↑ fmfiain: jarrro to může zkušet jak dlouho chce, ale pokud sem nedáš svůj postup, tak z toho nikdo nepoznáme, kde jsi udělal chybu. A chybu jsi udělat musel, pokud ti dvěma metodama vyšel různej determinant jedný matice.

fmfiain · 29. 12. 2018 11:57

↑ Stýv:
Dobrý deň,
tu je môj postup z prvej metódy (pomocou Sarrusovho pravidla):

//forum.matweb.cz/upload3/img/2018-12/80984_cele%2B%2BSarrusovo%2Bpravidlo.png

Potom ukážem aj tú druhú metódu.

Andrejka3 · 29. 12. 2018 13:06

↑ fmfiain:
Zapomínáš na znaménka při rozvoji podle řádku.

jardofpr · 29. 12. 2018 14:15

↑ fmfiain:

mne sa nezdajú ani tie minor matice

fmfiain · 31. 12. 2018 09:33

↑ Andrejka3:
Dobrý deň,
áno s tými znamienkami som to pokazil. Skúsim to vypočítať ešte raz.

fmfiain

↑ Andrejka3:
Dobrý deň,
posielam opravené riešenie cez Sarrusovo pravidlo.

//forum.matweb.cz/upload3/img/2018-12/50078_cele%2Bsarrusovo%2Bpravidlo%2B2.png

Dúfam, že to mám už dobre.

jardofpr · 31. 12. 2018 16:37

ahoj ↑ fmfiain:

znamienka si opravil dobre a výsledok máš správny, ale viac-menej náhodou lebo minory a teda rozvoj stále nemáš dobre

minor matica pri prvku $x_2-2$ má byť $\begin{bmatrix}0&0&1\\1&1&0\\1&1&0\end{bmatrix}$ a pri prvku $x_3-3$ má byť minor matica $\begin{bmatrix}0&1&1\\1&1&0\\1&0&0\end{bmatrix}$

fmfiain · 01. 01. 2019 09:47

↑ jardofpr:
Dobrý deň,
takže sa vypisujú stĺpce od najľavejšej po najpravejšiu:

//forum.matweb.cz/upload3/img/2019-01/32391_cele%2Bsarrusovo%2Bpravidlo%2B3.png

fmfiain

Dobrý deň,
toto riešenie je bez Sarrusovho pravidla:
$\begin{vmatrix} x_{1}-1 & x_{2}-2 & x_{3}-3 & x_{4}-4 \\ 0 & 1 & 0 & 1 \\ 1 & 1 & 1 & 0 \\ 1 & 0 & 1 & 0 \end{vmatrix} = 0$

$(x_{1}-1)(-1)^{2}\begin{vmatrix} 1 & 0 & 1 \\ 1 & 1 & 0 \\ 0 & 1 & 0 \\ \end{vmatrix} + (x_{2}-2)(-1)^{3}\begin{vmatrix} 0 & 0 & 1 \\ 1 & 1 & 0 \\ 1 & 1 & 0 \\ \end{vmatrix} + (x_{3}-3)(-1)^{4}\begin{vmatrix} 0 & 1 & 1 \\ 1 & 1 & 0 \\ 1 & 0 & 0 \\ \end{vmatrix} + (x_{4}-4)(-1)^{5} \begin{vmatrix} 0 & 1 & 0 \\ 1 & 1 & 1 \\ 1 & 0 & 1 \\ \end{vmatrix} = 0$

$(x_{1}-1)(-1)^{2}[(1)(-1)^{2}\begin{vmatrix} 1 & 0 \\ 1 & 0 \\ \end{vmatrix} + (0)(-1)^{3}\begin{vmatrix} 1 & 0 \\ 0 & 0 \\ \end{vmatrix} + (1)(-1)^{4}\begin{vmatrix} 1 & 1 \\ 0 & 1 \\ \end{vmatrix}] +\\ (x_{2}-2)(-1)^{3}[(0)(-1)^{2}\begin{vmatrix} 1 & 0 \\ 1 & 0 \\ \end{vmatrix} + (0)(-1)^{3}\begin{vmatrix} 1 & 0 \\ 1 & 0 \\ \end{vmatrix} + (1)(-1)^{4}\begin{vmatrix} 1 & 1 \\ 1 & 1 \\ \end{vmatrix}] + \\ (x_{3}-3)(-1)^{4}[(0)(-1)^{2}\begin{vmatrix} 1 & 0 \\ 0 & 0 \\ \end{vmatrix} + (1)(-1)^{3}\begin{vmatrix} 1 & 0 \\ 1 & 0 \\ \end{vmatrix} + (1)(-1)^{4}\begin{vmatrix} 1 & 1 \\ 1 & 0 \\ \end{vmatrix}] + \\ (x_{4}-4)(-1)^{5} [(0)(-1)^{2}\begin{vmatrix} 1 & 1 \\ 0 & 1 \\ \end{vmatrix} + (1)(-1)^{3}\begin{vmatrix} 1 & 1 \\ 1 & 1 \\ \end{vmatrix} + (0)(-1)^{4}\begin{vmatrix} 1 & 1 \\ 1 & 0 \\ \end{vmatrix} = 0$

$(x_{1}-1) + (x_{3}-3)(-1) = 0$

$x_{1} - x_{3} + 2 = 0$

Ospravedlňujem sa, že som neveril, že so Sarrusovím pravidlom a bez neho vyjde to isté. Opravil som tie znamienka.
Opravil som aj tu maticu 3x2 na 2x2.

jardofpr · 01. 01. 2019 14:16

ahoj ↑ fmfiain:

jednu maticu v tom rozvoji máš $3\times 2$ čo tam nemá byť
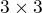okrem toho pri rozvoji na matice typu $2\times 2$ z matíc typu $3\times 3$ zabúdaš zasa na znamienka,
hoci výsledok máš náhodou správny

fmfiain · 03. 01. 2019 10:57

Dobrý deň,
dá sa Sarrusovo pravidlo použiť aj na matice väčšie ako 3x3, alebo treba vždy použiť rozvoj podľa Laplaceovej vety až na maticu 3x3.

Ďakujem za odpoveď.

jardofpr · 03. 01. 2019 12:13

ahoj ↑ fmfiain:

na väčšie matice sa nedá, najväčšia kde sa dá je 3x3

Matematické Fórum

#1 29. 12. 2018 09:28

Sarrusovo pravidlo vs Laplaceova veta o rozvoji determinantu

#2 29. 12. 2018 09:39

Re: Sarrusovo pravidlo vs Laplaceova veta o rozvoji determinantu

#3 29. 12. 2018 10:03

Re: Sarrusovo pravidlo vs Laplaceova veta o rozvoji determinantu

#4 29. 12. 2018 10:42

Re: Sarrusovo pravidlo vs Laplaceova veta o rozvoji determinantu

#5 29. 12. 2018 11:57

Re: Sarrusovo pravidlo vs Laplaceova veta o rozvoji determinantu

#6 29. 12. 2018 13:06

Re: Sarrusovo pravidlo vs Laplaceova veta o rozvoji determinantu

#7 29. 12. 2018 14:15

Re: Sarrusovo pravidlo vs Laplaceova veta o rozvoji determinantu

#8 31. 12. 2018 09:33

Re: Sarrusovo pravidlo vs Laplaceova veta o rozvoji determinantu

#9 31. 12. 2018 10:31 — Editoval fmfiain (31. 12. 2018 10:55)

Re: Sarrusovo pravidlo vs Laplaceova veta o rozvoji determinantu

#10 31. 12. 2018 16:37

Re: Sarrusovo pravidlo vs Laplaceova veta o rozvoji determinantu

#11 01. 01. 2019 09:47

Re: Sarrusovo pravidlo vs Laplaceova veta o rozvoji determinantu

#12 01. 01. 2019 11:32 — Editoval fmfiain (02. 01. 2019 08:40)

Re: Sarrusovo pravidlo vs Laplaceova veta o rozvoji determinantu

#13 01. 01. 2019 14:16

Re: Sarrusovo pravidlo vs Laplaceova veta o rozvoji determinantu

#14 03. 01. 2019 10:57

Re: Sarrusovo pravidlo vs Laplaceova veta o rozvoji determinantu

#15 03. 01. 2019 12:13

Re: Sarrusovo pravidlo vs Laplaceova veta o rozvoji determinantu

Zápatí