Matematické Fórum

MichalAld · 10. 02. 2019 10:43

Zrovna v jednom fyzikálním vlákně řešíme, zdali může mít Laplaceova rovnice

$\triangle \varphi = 0$

s okrajovou podmínkou, že v nekonečné vzdálenosti od počátku je její hodnota nulová, tedy že

$\varphi_{(\infty )} = 0$

a asi ještě s požadavkem, že řešení musí v celém prostoru existovat (tj. nesmí tam být nějaké body nespojitosti)

zdali může mít i jiné řešení, nežli nulové v celém prostoru, nebo nemůže.

Nepotřebujeme důkaz, stačil by odkaz, nebo aspoň názor.

laszky · 10. 02. 2019 13:47

↑ MichalAld:

Ahoj, me napadaji napr. tyto 2 duvody:

1) Jelikoz je $L=-\Delta$ elipticky operator, plati pro nej srovnavaci princip:

$L\varphi\geq0\;\mbox{v}\ \Omega\;\;\& \;\; \varphi\geq0\;\mbox{na}\ \partial\Omega\quad\Rightarrow\quad \varphi\geq0\;\mbox{v}\ \overline{\Omega}$

Pouzije-li se stejne pravidlo na funkci $-\varphi$ , ziskame

$\varphi\geq0\;\mbox{v}\ \overline{\Omega}\;\; \& \;\; \varphi\leq0\;\mbox{v}\ \overline{\Omega}\quad\Rightarrow\quad \varphi=0\;\mbox{v}\ \overline{\Omega}$

2) Napr. Greenova funkce pro Laplaceuv operator v 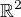$\mathbb{R}^2$ ma tvar

$G(x_1,x_2) = \frac{1}{2\pi}\,\sqrt{x_1^2+x_2^2}$

a reseni rovnice $\Delta \varphi = f\;\mbox{v}\ \mathbb{R}^2$ s $\varphi_{(\infty )} = 0$ lze vyjadrit ve tvaru

$\varphi(x_1,x_2)=\int_{\mathbb{R}^2} G(x_1-\overline{x}_1,x_2-\overline{x}_2)f(\overline{x}_1,\overline{x}_2)\,\mathrm{d}\overline{\boldsymbol{x}}$

Je-li $f=0$ , je i $\varphi=0\;\mbox{v}\ \mathbb{R}^2$ .

KennyMcCormick · 10. 02. 2019 23:54

Platí to i pro vektorový Laplaceův operátor?

Bati · 13. 02. 2019 10:24 — Editoval Bati (13. 02. 2019 10:25)

Ahoj, tady je jedno, jestli je to skalarni rovnice nebo vektorova, protoze laplac po slozkach je zase laplac a prava strana je nula.

Jinej zpusob jak to videt je, ze kazda harmonicka funkce splnuje mean value property:
$\varphi(x)=\frac1{r^{n-1}V_d}\int_{\partial B_r(x)}\varphi(y)\,\mathrm{d}S(y)$
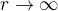Takze $|\varphi(x)|\leq \sup_{\partial B_r}|\varphi(y)|\to0$ , $r\to\infty$ , pro kazdy $x$ .

Zadny pozadavek spojitosti neni potreba, mas hezkou pravou stranu a okrajovky, takze reseni existuje a je hladky

MichalAld · 13. 02. 2019 23:04

Bati napsal(a):
Zadny pozadavek spojitosti neni potreba, mas hezkou pravou stranu a okrajovky, takze reseni existuje a je hladky

No jo, ale co když vezmu třeba funkci

$F(z) = \frac{1}{z}=\frac{1}{x+iy} = \frac{x}{x^2+y^2}-i\frac{y}{x^2+y^2}$

Rovnici by měla (krom bodu nula) splňovat - každá "slušná" komplexní funkce by ji měla splňovat, a nuly to v nekonečné vzdálenosti nabývá také. Akorát je tam ta nespojitost v bodě nula. Proto jsem předpokládal, že požadavek na spojitost v celé oblasti je nutný.

Bati · 14. 02. 2019 00:40

To je fakt...dalsi duvod, proc na celym $R^d$ je to hrozne divny...

MichalAld · 17. 02. 2019 15:02

Bati napsal(a):
To je fakt...dalsi duvod, proc na celym $R^d$ je to hrozne divny...

Nepřijde mi, že by to příliš souviselo s tím, že je hledáme řešení v celém R^3.

Třeba ta funkce, co jsem zmínil,

$F(x,y) = \frac{x}{x^2+y^2}$

bude řešením i na nějaké oblasti obsahující počátek, pokud si vhodně zvolíme okrajové podmínky (aby jí vyhovovaly).

Nevím samozřejmě, jestli pro libovolnou volbu okrajových podmínek dokážeme najít funkci, co má uvnitř té oblasti nějaký "pól" či jak se tomu říká. Ale pro nějaké okrajové podmínky to lze určitě.

Proto si myslím, že požadavek na spojitost v té oblasti, kde řešení hledáme, je podstatný. Nebo prostě požadavek na to, aby řešení existovalo v celé té oblasti.

Matematické Fórum

#1 10. 02. 2019 10:43

Laplaceova rovnice

#2 10. 02. 2019 13:47

Re: Laplaceova rovnice

#3 10. 02. 2019 23:54

Re: Laplaceova rovnice

#4 13. 02. 2019 10:24 — Editoval Bati (13. 02. 2019 10:25)

Re: Laplaceova rovnice

#5 13. 02. 2019 23:04

Re: Laplaceova rovnice

Bati napsal(a):

#6 14. 02. 2019 00:40

Re: Laplaceova rovnice

#7 17. 02. 2019 15:02

Re: Laplaceova rovnice

Bati napsal(a):

Zápatí