Matematické Fórum

Marvv · 18. 10. 2009 21:10

Prosím o radu jakým směrem se ubírat, jaké vzorečky použít a k jakému výsledku by jsem měl dojít, díky moooc :).

Zadání:
Zjistětě střední hodnotu, kolik jogurtů musíme koupit aby jsme měli všechny 4 obrázky, které jsou u nich přibaleny a to u každého právě jeden.
a zjistětte Var téhož.

check_drummer · 18. 10. 2009 21:43

Spočítat pravděpodobnost, že když koupím k jogurtů, tak budu mít všechny 4 obrázky (některé eventuelně vícekrát) - tento počet označme P(k). Střední hodnota bude součet k.P(k) pro k od 1 do nekonečna.

Marvv · 18. 10. 2009 21:46 — Editoval Marvv (18. 10. 2009 21:47)

Dal by se na to nějak napasovat vzoreček pro geometrickou distribuci - počet akcí než nastane kýžený jev?

jelena · 19. 10. 2009 15:56

↑ Marvv: zdravím, obdobný problém se řeší zde - úloha 7..

Stejná úloha už zde na foru byla (čokoladová zvířatka), ale kolega Fin všechno smazal (hodně toho smazal, není nad pořadkumilovnost), ale neformuloval, že se jedná o střední hodnotu (ovšem kolega Kondr tuto variantu zadání navrhoval) - teď je zadání jednoznačné.

Marvv · 19. 10. 2009 18:51

Mohl bych mooc poprosit o konkrétní výpočet an tento příklad, ať vím, jestli jsem se dobádal ke správnému číslu? A jak by to bylo s tou Variací?

jelena · 19. 10. 2009 22:49 — Editoval jelena (19. 10. 2009 22:50)

↑ Marvv:

to už jen opakuji, co se povídalo: ↑ check_drummer: a kolega Kondr v příspěvku, který Fin smazal.

1) střední hodnota se bude počítat jako součet středních hodnot jednotlivých jevů - dle vlastností střední hodnoty součtu:

$\operatorname{E}(X_1+X_2+X_3+X_4)=\operatorname{E}(X_1)+\operatorname{E}(X_2)+\operatorname{E}(X_3)+\operatorname{E}(X_4)$

X_1 - hned v prvním nákupu mám jeden obrazek (pravděpodobnost takového jevu je 1, E(X_1=1/p=1/1)
X_2... X_4 - v dalších nákupech se pravděpodobnost, že dostanu požadovaný obrazek je menší a dle vzoru ve cvičení v odkazu a dle Wikipedie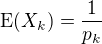

$\mathrm{E}(X_k) = \frac{1}{p_k}$ , ${p_k}=\frac{4-k}{4}$ , k=1, 2, 3

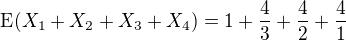$\operatorname{E}(X_1+X_2+X_3+X_4)=1+\frac{4}{3}+\frac{4}{2}+\frac{4}{1}$ souhlasi?

Ona "ta variace" je v českých poměrech "ten rozptyl" (vy se učite z anglických materiálů? - alespoň orientačně, kde jsou takové vymoženosti?)

A teď uvažuji - pokud je střední hodnota součtu, tak i rozptyl by se měl počítat pro součet - nebo jak? Pokud douvažuji, tak to zedituji (ale nevzpomínám si, že jsem kdy douvažovala k něčemu kloudnému)

---------------------------------
Pro vážené Moderatorstvo - jelikož jsem pouze opsala postupy a návody od vás a z odkazu (tak prosím překontrolovat a zpřipomínkovat nebo schvalit, pokud je to v pořádku a není nutné přesouvat) a děkuji za zastání- snahu jsem měla, dnes ovšem nemám náladu něco diskutovat. Zdravím.

Kondr · 20. 10. 2009 00:58

↑ jelena:Taky se přikláním k tomu, že variace bude to samé, co rozptyl (viz anglický ekvivalent), takže je to také aditivní veličina a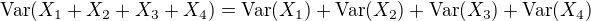
$\operatorname{Var}(X_1+X_2+X_3+X_4)=\operatorname{Var}(X_1)+\operatorname{Var}(X_2)+\operatorname{Var}(X_3)+\operatorname{Var}(X_4)$ . Pro variace jednotlivých jevů stačí dosadit rozptyl geometrického rozdělení z odkazu.

----
A samozřejmě pozdrav :o) ...

Marvv · 20. 10. 2009 05:37

Jelena - dekuiji moc, jsem asi ale natvrdly, porad nevim co do te variace dosadit - do jakeho vzorce - pro stredni hodnotu jsme meli 1-p/p ale tady se to pritom pocita pouze 1/p. Tak nevim jestli u te var vychazet z 1-p/p^2 nebo z ceho :-(

jelena · 20. 10. 2009 09:16

↑ Marvv:

zdravím, podívej se na odkaz z anglické wikipedie - vzorec pro Var je stejný (jen jeden), tak jak uvádiš. Jinak zkus pohledat podle slov Collector problem (nebo podobně) - třeba něco takového, str. 10

V zadání máš, že je potřeba najit 4 obrazky - proto jednotlivé střední hodnoty (vypočtené dle vzorce pro E ještě navzájem sčítáme). Bohužel, mám omezené časové možnosti na něco rozsahlejšího.

pro kolegu Kondra: děkuji :-)

Matematické Fórum

#1 18. 10. 2009 21:10

Výpočet střední hodnoty

#2 18. 10. 2009 21:43

Re: Výpočet střední hodnoty

#3 18. 10. 2009 21:46 — Editoval Marvv (18. 10. 2009 21:47)

Re: Výpočet střední hodnoty

#4 19. 10. 2009 15:56

Re: Výpočet střední hodnoty

#5 19. 10. 2009 18:51

Re: Výpočet střední hodnoty

#6 19. 10. 2009 22:49 — Editoval jelena (19. 10. 2009 22:50)

Re: Výpočet střední hodnoty

#7 20. 10. 2009 00:58

Re: Výpočet střední hodnoty

#8 20. 10. 2009 05:37

Re: Výpočet střední hodnoty

#9 20. 10. 2009 09:16

Re: Výpočet střední hodnoty

Zápatí