Matematické Fórum

xkaca100 · 19. 12. 2009 21:15

Ahoj, prosím o pomoc s tímhle příkladem. Asi je to primitivní, ale já jsem to ve škole nějak nepochopila. Pokaždé mi vyjde jiný výsledek. Nevím co je správně. Dík

http://forum.matweb.cz/upload/126125350 … brazce.jpg

halogan

Funkce si nakresli, najdi jejich průsečíky a počítej integrál.

Jo a řekni nám, co ti vyšlo.

xkaca100 · 19. 12. 2009 21:58

↑ halogan:
dolní mez -1, horní mez 6 a obsah 55,7

jelena · 20. 12. 2009 01:53

↑ xkaca100:

mez - souhlasí, obsah plochy mi vychází 114,3 - zkus sem umístit svůj postup výpočtu, proč máme rozdílné výsledky? Děkuji.

xkaca100

↑ jelena:

Počítala jsem to ještě jednou a vyšlo mi to takhle....

http://forum.matweb.cz/upload/1261311648-100_8306.JPG

jelena · 20. 12. 2009 13:46

↑ xkaca100:

Zdravím, ty počítáš obsah plochy omezené takovou křívkou (navíc, křívka je pod osou x, tedy v integralu má být absolutní hodnota, obsah nemůže být záporný), ale to vůběc není tvé zadání.

Máš počítat obsah takového obrazce.. Je to srozumitelné?

xkaca100 · 20. 12. 2009 14:42

↑ jelena:
my se to ale s absolutní hodnotou neučili...

halogan · 20. 12. 2009 14:50

↑ xkaca100:

Máš tam (-5)^3, má tam ale být (-5)^2.

Ale je tam úplně zásadní a fatální chyba. Nemůžeš jen tak celý předpis funkce vydělit dvěma, to prostě nejde. Jinak dobré.

jelena · 20. 12. 2009 16:23

↑ halogan:

Zdravím,

co je na tom "jinak dobre"? - v zápisu má být "horní funkce 10x-x^2" - "dolní funkce x^2-12", ovšem ve skutečnosti je to celé vyděleno (-2).

Jinak pozoruji, že jsem již zcela zhlouplá - Rektorys (obr. 14.24, str. 539), Bartsch a Wikipedie požaduji, že pokud odečitam "dolní" od "horní", musí platit podmínka, že obě funkce mají mít kladné hodnoty. Naše s kolegou O.o oblibená kniha ovšem žádné takové omezení nepožaduje nebo povídá něco, čemu nerozumím.

Já jsem cvičně počítala na jednotlivé oblasti a přes rozdíl funkcí, výsledek je stejný. Tak mi, prosím, řeknete, jak je to s podmínkou, že hodnoty všech funkcí f(x), g(x) maji být kladné (vůběc to nehoří, stačí v srpnu). Děkuji.

halogan · 20. 12. 2009 16:32

↑ jelena:

Jinak dobré, že jinak chápe postup, jen použil špatné funkce. Možná jsem ho přechválil :-)

Jinak se do toho raději více pouštět nebudu, protože na teorii jsem se už jednou ptal a nemám na to tolik znalostí. Čeká mě to až za 2 semestry.

xkaca100 · 20. 12. 2009 17:20

↑ halogan:
tak teď jsem teda uplně zmatená.... prosím prosím... je možné poslat ten postup celý?

jelena · 20. 12. 2009 17:31 — Editoval jelena (21. 12. 2009 10:59)

↑ xkaca100:

jelikož tady nesmyslnou debatu začínám já, tak to napravím a napiši to v souladu s knihou y VŠCHT:

$S = \int_a^b f(x)\mathrm{d}x -\int_a^b g(x)\mathrm{d}x = \int_a^b \left[f(x)-g(x)\right]\mathrm{d}x$ vzorec kopírován z Wikipedie v posledním platném vydání
$S =\int_{-1}^6 \left[10x-x^2-$x^2-12$\right]\mathrm{d}x =\int_{-1}^6 \left[10x-2x^2+12\right]\mathrm{d}x$

to je funkce k integrování (jak je to s podmínkou nezápornosti, snad mi někdo vysvětlí).

Integrovat umíš, potvrzuje to kolega.

Olin · 20. 12. 2009 17:40 — Editoval Olin (20. 12. 2009 17:43)

Je jasné, že když k oběma ohraničujícím funkcím přičteme tutéž konstantu, dostaneme tutéž oblast, jen nějak posunutou ve směru osy y, takže její obsah bude stejný jako obsah oblasti, který hledáme. Podívejme se, jak se to projeví např. na našich funkcích,
$p(x) = 10x-x^2\nl q(x) = x^2-12$
když k nim přičteme třeba 20:
$\tilde{p}(x) = 10x - x^2 + 20\nl \tilde{q}(x) = x^2 +8$
Viz grafy.

Z tohoto je již patrné, že můžeme obsah oblasti vypočítat jako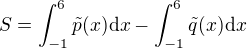
$S = \int_{-1}^6 \tilde{p}(x) \mathrm{d} x - \int_{-1}^6 \tilde{q}(x) \mathrm{d} x$ ,
což však díky linearitě integrálu můžeme upravit na
$S = \int_{-1}^6 $\tilde{p}(x) - \tilde{q}(x)$ \mathrm{d} x = \int_{-1}^6 $p(x) + 20 - q(x) - 20$ \mathrm{d} x = \int_{-1}^6 $p(x) - q(x)$ \mathrm{d} x$ .

Stačí tedy zintegrovat rozdíl funkcí.

EDIT: Teď si pozorněji pročítám diskusi předtím, no, snad jsem objasnil tu záhadu, proč se nemusíme (aspoň v tomto případě) zabývat nějakými znaménky.

xkaca100 · 20. 12. 2009 19:10

díky za radu, teď jsem to přepočítala a vyšlo mi 114,33

Olin · 20. 12. 2009 19:48

Je to tak, $\frac{343}{3}$ .

jelena · 20. 12. 2009 21:56

↑ Olin: potěšující shoda ↑ jelena:, děkuji :-)

kaja(z_hajovny)

jelena napsal(a):
Já jsem cvičně počítala na jednotlivé oblasti a přes rozdíl funkcí, výsledek je stejný. Tak mi, prosím, řeknete, jak je to s podmínkou, že hodnoty všech funkcí f(x), g(x) maji být kladné (vůběc to nehoří, stačí v srpnu). Děkuji.

Pěkný den, do sprna daleko, ale i tak .......

Pro libovolnou konstantu c plati

$\int f(x)-g(x) dx = \int [f(x)+c]-[g(x)+c] dx$

A pokud by teda funkce f(x) nebo g(x) nebyly nezaporne, da se k nim pricist cislo c (k oboum funkcim stejne), tak, aby funkce f(x)+c a g(x)+c nezaporne byly. Integral vyjde stejne. Podminka $0\leq g(x)\leq f(x)$ se ve vzorci z wikipedie tedy da zeslabit na $g(x)\leq f(x)$ a proto jsem to opravil i na Wikipedii. Ted uz by to tam melo byt spravne a dokonce v souladu s obrazkem (pouvodne prohozene f a g).

jelena · 21. 12. 2009 10:57

↑ kaja(z_hajovny):

Zdravím Vás a děkuji, teď bych mohla být v naprostém klidu - ale co edit Rektoryse a Bartsche?

Jak to vzniklo? - došla jsem v nočních hodinách zasněženou Opavou z práce a jen tak jsem relaxovala, vypočetla jsem standardním způsobem jako rozdíl "horní"-"dolní", výsledek jsem si zkontrolovala na Wolfram, ale když jsem chtěla vykopírovat vyTeXaný vzorec z Wikipedie, tak takový šok (a když jsem stejnou podmínku našla i v knize...). Tak jsem celá vyšokovana přepočetla na jednotlivé díly, po nějaké době jsem také došla na posun osy x, jak navrhuje kolega ↑ Olin: (pochodovat Opavou zpět k analytické váze se mi už nějak nechtělo) a až poté jsem umístila svůj výsledek ↑ jelena:. Teď ještě ve shodě s Vaši opravou budu editovat vzorec vykopirovaný z Wikipedie.

Kde a proč to tedy Bartsch s Rektorysem sebrali?

"vůběc to nehoří, stačí v srpnu" - to tak nějak vzniklo s našimi programátory, že do leta všechno udeláme, ať mohu v letě psát zprávy o překonání obtíží a manuály (žádný informatik mi nechce psát manuály, jenže my podle předpisů musíme, tak to napíši sama) a standardy. Tento rok máme v podstatě všechno hotovo, až na jeden nový modul - který měl být v červenci, pak "bla-bla" až do 5. prosince. Minulý týden jsem lehce přitvrdila hlas a výsledek - na třetí den jsem měla místo PF hotovou zprávu o kontrole systému, kterou očekávám od srpna, a přislib, že mezi svátky dojedou - dobře jim tak, mohli v srpnu.

Ještě máme "umyt nádobí" - to když se udělá hodně změn, co není vidět, a pak jedna nenáročná, ale efektní - nějaka tisková sestava, kterou někdo požadoval.

Mějte se hezky a děkuji :-)

Matematické Fórum

#1 19. 12. 2009 21:15

Určitý intgrál - obsah obrazce, který je ohraničený křivkami

#2 19. 12. 2009 21:23 — Editoval halogan (19. 12. 2009 21:23)

Re: Určitý intgrál - obsah obrazce, který je ohraničený křivkami

#3 19. 12. 2009 21:58

Re: Určitý intgrál - obsah obrazce, který je ohraničený křivkami

#4 20. 12. 2009 01:53

Re: Určitý intgrál - obsah obrazce, který je ohraničený křivkami

#5 20. 12. 2009 13:21 — Editoval xkaca100 (20. 12. 2009 13:22)

Re: Určitý intgrál - obsah obrazce, který je ohraničený křivkami

#6 20. 12. 2009 13:46

Re: Určitý intgrál - obsah obrazce, který je ohraničený křivkami

#7 20. 12. 2009 14:42

Re: Určitý intgrál - obsah obrazce, který je ohraničený křivkami

#8 20. 12. 2009 14:50

Re: Určitý intgrál - obsah obrazce, který je ohraničený křivkami

#9 20. 12. 2009 16:23

Re: Určitý intgrál - obsah obrazce, který je ohraničený křivkami

#10 20. 12. 2009 16:32

Re: Určitý intgrál - obsah obrazce, který je ohraničený křivkami

#11 20. 12. 2009 17:20

Re: Určitý intgrál - obsah obrazce, který je ohraničený křivkami

#12 20. 12. 2009 17:31 — Editoval jelena (21. 12. 2009 10:59)

Re: Určitý intgrál - obsah obrazce, který je ohraničený křivkami

#13 20. 12. 2009 17:40 — Editoval Olin (20. 12. 2009 17:43)

Re: Určitý intgrál - obsah obrazce, který je ohraničený křivkami

#14 20. 12. 2009 19:10

Re: Určitý intgrál - obsah obrazce, který je ohraničený křivkami

#15 20. 12. 2009 19:48

Re: Určitý intgrál - obsah obrazce, který je ohraničený křivkami

#16 20. 12. 2009 21:56

Re: Určitý intgrál - obsah obrazce, který je ohraničený křivkami

#17 21. 12. 2009 07:59 — Editoval kaja(z_hajovny) (21. 12. 2009 08:11)

Re: Určitý intgrál - obsah obrazce, který je ohraničený křivkami

jelena napsal(a):

#18 21. 12. 2009 10:57

Re: Určitý intgrál - obsah obrazce, který je ohraničený křivkami

Zápatí