Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Rychlokurz počítání elementárních limit funkcí (TOTO TÉMA JE VYŘEŠENÉ)
#1 03. 01. 2010 22:27 — Editoval halogan (04. 01. 2010 09:15)
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Rychlokurz počítání elementárních limit funkcí
Nějak se často lidé ptají na limitění, tak jsem se rozhodl napsat takový rychlokurz, takový semestr v neuhlazené kostce :-) Je to psané dosti obecně, nepřesně (kdybych měl vše ošetřovat, tak to bude 5x delší) a neodborně (na to nemám znalosti), ale přímo mystifikovat by to nemělo. Několik částí tam chybí, časem je dopíši. Ještě tu spousta věcí chybí, ale už jsem nějak unaven, píšu to už skoro dvě hodiny. Nekoukal jsem do skript, ale asi jsem spoustu věcí zapomněl či popletl, budu rád za korekci. Třeba limita e^{...} tu vůbec není rozvedena.
Pokud to bude k něčemu užitečné, tak sem přidám nějaké anchory, ať se na to dá odkazovat.
---
Nejde tady na rozumném rozsahu (už toto má skoro 6 normostran) obsáhnout vše, vynechávám tedy věci, které byste měli znát (operace v oboru R* apod.).
1) SPOJITOST A DOSAZOVÁNÍ.
Co je to vlastně limita? Zjednodušeně by se dalo říct, že zkoumáme, k jaké funkční hodnotě se funkce blíží, pokud se blížíme k nějaké zadané hodnotě nezávislé proměnné. Nás sice nezajímá, jakou hodnotu má v zadaném bodě (či zda je tam vůbec definovaná), ale pokud je funkce spojitá, tak se logicky bude z obou stran k funkční hodnotě v zadaném bodě blížit. Výpočet je pak velice snadný - dosazení - takovou radost nám však zadavatelé dávají jen velice zřídka.
2) DODEFINOVÁNÍ.
Mějme následující limitu: .
.
Po dosazení zjistíme, že ve dvojce není funkce definovaná, budeme se tedy snažit funkci nějak upravit. Ze střední školy umíme jmenovatel (kvadratická funkce) složit na součin  . Teď bychom mohli krátit... ale můžeme?
. Teď bychom mohli krátit... ale můžeme?
Můžeme si jen tak upravit předpis limity?  v čitateli i ve jmenovateli má vždy stejnou hodnotu, ať do tohoto výrazu dosadíme cokoliv. Jediný problém nastává, když
v čitateli i ve jmenovateli má vždy stejnou hodnotu, ať do tohoto výrazu dosadíme cokoliv. Jediný problém nastává, když  . Dostáváme 0/0, což není definovnáno. Můžeme se jen tak zbavit nedefinovaného výrazu? Můžeme, protože funkce nás ve dvojce "nezajímá", počítáme limitu v jejím okolí. Všude jinde hodnotu funkce neměníme, takže můžeme limitu dál počítat.
. Dostáváme 0/0, což není definovnáno. Můžeme se jen tak zbavit nedefinovaného výrazu? Můžeme, protože funkce nás ve dvojce "nezajímá", počítáme limitu v jejím okolí. Všude jinde hodnotu funkce neměníme, takže můžeme limitu dál počítat.
Počítáme teď limitu funkce, která je nově ve dvojce spojitá, dodefinovali jsme si ji tam: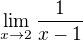 a vychází nám hezká jednička.
a vychází nám hezká jednička.
3) VYTÝKÁNÍ.
V předchozím bodě jsme počítali s limitou ve vlastním bodě, teď se v rychlosti podíváme na limitu v nevlastním bodě (teorii si doplňte sami).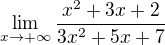
Čitatel i jmenovatel nám jdou do nekonečna, to nepotěší. My teď musíme rozhodnout, jak jsou ta nekonečna "velká". S rostoucím  nám obě funkce rostou a uvidíte, že lineární a absolutní členy budou mít časem čím dál menší důležitost a dominantní část hodnoty bude vytvářet právě kvadratický člen. Vytkneme jej tedy.
nám obě funkce rostou a uvidíte, že lineární a absolutní členy budou mít časem čím dál menší důležitost a dominantní část hodnoty bude vytvářet právě kvadratický člen. Vytkneme jej tedy.
Když teď  pokrátíme (z předchozí kroku již víme, že můžeme, pokud nám x jde do nekonečna), tak zjistíme, že v čitateli nám zbývá "1 a nějaké zbytky, které půjdou k nule" a ve jmenovateli zbyde "3 a též nějaké zbytky". Ty "zbytky" poznáme tak, že jim nekonečně roste jmenovatel a čitatel je nějaká konstanta. Podíl reálné konstanty a nekonečna je 0. V šesté části tohoto rychlokurzu se naučíte trochu elegantnějšího určení této limity.
pokrátíme (z předchozí kroku již víme, že můžeme, pokud nám x jde do nekonečna), tak zjistíme, že v čitateli nám zbývá "1 a nějaké zbytky, které půjdou k nule" a ve jmenovateli zbyde "3 a též nějaké zbytky". Ty "zbytky" poznáme tak, že jim nekonečně roste jmenovatel a čitatel je nějaká konstanta. Podíl reálné konstanty a nekonečna je 0. V šesté části tohoto rychlokurzu se naučíte trochu elegantnějšího určení této limity.
Limita tedy vyjde 1/3.
3B) URČENÍ DOMINANTNÍHO ČLENU.
Abychom mohli vytknout nějaký člen, pokrátit jej a zbytek poslat do nuly, musíme vědět, který člen to je. Co roste rychleji než něco jiného. Poslouží tento seznam nerovností. "<<" znamená prudkou (TODO) nerovnost - tj. že jedna funkce bude časem nabývat mnohem větších hodnot.
Mějme proměnnou  , která jde do nekonečna a nějaké reálné konstanty
, která jde do nekonečna a nějaké reálné konstanty  a
a  , obě větší než 1.
, obě větší než 1.
n << n^k << a^n << n! << n^n
Slovy řečeno - lineární funkce << polynom (k by v tomto případě melo být přirozené číslo) << exponenciální funkce << faktoriál << n^n :-)
Budeme tedy mít limitu: .
.
Vytkneme 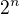 , pokrátíme, čitatel jde k jedničce, jmenovatel jde do nekonečna (zbylo nám tam
, pokrátíme, čitatel jde k jedničce, jmenovatel jde do nekonečna (zbylo nám tam 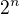 ), výsledek je nula.
), výsledek je nula.
4) ODMOCNINY
Mějme limitu: .
.
Vychází nekonečno minus nekonečno. Jak se zbavit odmocnin? To jistě znáte z usměrňování zlomků. Stačí šikovně rozšířit. V tomto případě zlomkem, který bude mít v čitateli i jmenovateli 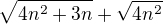 . Dostaneme tak náběh na vzorec
. Dostaneme tak náběh na vzorec  . Dostáváme tak:
. Dostáváme tak:
Zde jsem udělal dvě úpravy najednou. V čitateli jsem použil vzorec a ve jmenovateli jsem z odmocnin (obě šly do nekonečna) vytknul dominantní člen, který pak mohu krátit s tím v čitateli. Opět mi zbydou jen "zbytky", u kterých víme, kam míří.
---
Podobně budeme pracovat s výrazem např. ![kopírovat do textarea $\sqrt[3]{\dots} - \sqrt[3]{\dots}$](/mathtex/a0/a0565b36397f2f269379700f2fb7884c.gif) , jen budeme muset rozšířit tak, abychom v čitateli dostali
, jen budeme muset rozšířit tak, abychom v čitateli dostali 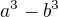 . Využijeme následující vzorec:
. Využijeme následující vzorec:
TODO
5) DVA POLICAJTI.
TODO
6) TABULKOVÉ LIMITY.
U některých složitějších limit budeme používat některé tabulkové limity. Jejich důkazy zde vypisovat nebudu, často se jedná o L'Hospitalovo pravidlo (popsané v deváté sekci).
Zkuste si jednotlivé limity nakreslit, ať víte, co znamenají geometricky.
A) 
B) 
C) 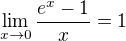
D) 
E) 
F)  (díky dalšímu kroku tuto limitu tolik potřebovat nebudeme)
(díky dalšímu kroku tuto limitu tolik potřebovat nebudeme)
Je celkem běžné, že v úvodu do matematické analýzy je spousta limit šroubována na tyto tabulkové limity, takže jejich výpočet nedá tolik práce. Ale k tomu se ještě dostaneme.
7) ČÁSTEČNÉ LIMITĚNÍ A OBECNÁ MOCNINA.
Častou chybou je, že se student snaží "zlimitit" část výrazu a zbytek až později. To jde však jen za přesně stanovených podmínek (o kterých si řekneme v dalších krocích) a je třeba je v písemce či u zkoušky okomentovat.
Proto pokud máme limitu: ,
,
nemůžeme si říct "závorka jde do jedničky a jednička na něco velkýho bude furt jednička". Tak to nefunguje. Musíme použít nějaký jiný způsob
---
Co se týče obecné mocniny, tak ta nám pomáhá počítat limity s exponenciálními funkcemi  , kde
, kde  je kladná konstanta a
je kladná konstanta a  je nezávislá proměnná. Moc neumíme s takovými výrazy pracovat, pokud si však uvědomíme, proč platí následující rovnost:
je nezávislá proměnná. Moc neumíme s takovými výrazy pracovat, pokud si však uvědomíme, proč platí následující rovnost:  (za podmínek, které jsem psal), tak společně se znalostí limity složené funkce (devátá část) nám vše půjde mnohem snadněji.
(za podmínek, které jsem psal), tak společně se znalostí limity složené funkce (devátá část) nám vše půjde mnohem snadněji.
8) ARITMETIKA LIMIT.
Mějme dvě funkce, f(x) a g(x) a nechť v bodě  mají limity A, resp. B, které patří do rozšířeného oboru reálných čísel (
mají limity A, resp. B, které patří do rozšířeného oboru reálných čísel ( ). Pak platí:
). Pak platí:
Pokud jsou výrazy na pravé straně definovány!
Aritmetiku limit je potřeba pořádně absorbovat, budete ji používat často. Jde o to, že si funkci mohu "roztrhnout" na více funkcí, pokud každá z dílčích "subfunkcí" má svou limitu a celkový součet/součin/podíl limit je definován.
Pozor tedy na výrazy 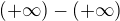 ,
,  ,
, 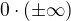 , ... a na případ, kdy limita některé ze "subfunkcí" neexistuje!
, ... a na případ, kdy limita některé ze "subfunkcí" neexistuje!
9) LIMITA SLOŽENÉ FUNKCE.
Nechť máme opět dvě funkce - g(x) a f(y) a existují limity:
A platí alespoň jedna z následujících podmínek:
P) Funkce g se na prstencovém okolí bodu c vyhýbá své limitě A. Tj.  .
.
S) Funkce f je spojitá v A.
Pak platí  .
.
---
Zde je též potřeba větu pořádně pochopit. Jde nám o to, že pokud nám vnitřní funkce jde k nějaké hodnotě a my v této hodnotě známe limitu vnější funkce (a platí alespoň jedna z daných podmínek), rovná se limita složené funkce té limitě vnější funkce.
---
Použití v praxi najdete v poslední části tohoto rychlokurzu.
10) L'HOSPITALOVO PRAVIDLO.
TODO
11) PRAXE.
Zde budu jen heslovitě popisovat jednotlivé kroky při řešení některých složitějších limit.
A) 
S logaritmem známe jen jednu limitu a zde vidíme, že nám argument (celkem pěkně) jde do jedničky, použijeme tedy limitu složené funkce (s limitou D) - splněna je podmínka P. Abychom ji však mohli použít, potřebujeme něco speciálního ve jmenovateli. Rozšíříme tedy.
První zlomek nám jde do jedničky, přes aritmetiku si to rozdělíme na součin dvou limit (každá limita limití jeden ze zlomků) a počítáme: (limita F)
(limita F)
->  .
.
B) 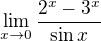
Jak si zvyknete na aritmetiku, začnete ji používat trochu jinak, protože např. tabulková limita A se sinem nám vlastně říká "funkce f(x) = sin x a g(x) = x se chovají kolem nuly celkem podobně, můžeme je tedy v limitě k nule mezi sebou měnit", zjednodušeně.
Rozšířili jsme x/x, druhý zlomek (přes limitu podílu) jde k jedničce, tak jej pomocí aritmetiky oddělíme a počítáme limitu zbytku. Využijeme toho, že sice neumíme pracovat s exp. funkcemi, ale můžeme si je přepsat pomocí znalosti obecné mocniny.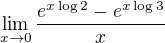
Tady to vypadá na tabulkovou limitu C, ale chybí nám tam ty jedničky... tak si je tam dopíšeme.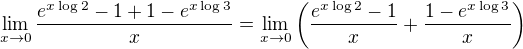
Teď už se jedná jen o hrátky s limitou složené funkce.
TODO další příklady.
------
Teď už stačí jen používat výše zmíněná pravidla a věty a počítat, počítat, počítat, časem si na ně zvyknete. Hodně štěstí.
Offline
- (téma jako vyřešené označil(a) Tychi)
#2 04. 01. 2010 07:50
Re: Rychlokurz počítání elementárních limit funkcí
↑ halogan:
Oceňujem tvoju námahu a konečne tu máme seriózny materiál, na ktorý bude možné odkazovať prípadných nešťastníkov. Pár chýb ale môjmu oku (pod taktovkou Mariana) neuniklo.
4) ODMOCNINY
- oprav v menovateli limity výraz 
8) ARITMETIKA LIMIT
- nesúhlasím s množinou  . Síce tam je poznámka - Pokud jsou výrazy na pravé straně definovány!, ale známa veta o súčte, rozdiele, súčine a podiele predpokladá existenciu vlastných limít. T.j. Nech ... a ... sú vlastné, potom ...
. Síce tam je poznámka - Pokud jsou výrazy na pravé straně definovány!, ale známa veta o súčte, rozdiele, súčine a podiele predpokladá existenciu vlastných limít. T.j. Nech ... a ... sú vlastné, potom ...
- pri podiele 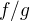 nemôže byť
nemôže byť 
9) LIMITA SLOŽENÉ FUNKCE
- doplnil by som tretiu možnosť 
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#3 04. 01. 2010 09:19
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Rychlokurz počítání elementárních limit funkcí
4) Překlep, díky.
8) Co pak ale s limitami divergentních funkcí? Jak je poznáme, když na začátku nebudou vypadat moc divergentně? :-) Rozšíření aritmetiky o +-\infty není důkazově moc náročné a funguje to. Pokud lim g(x) = 0, tak nebude výraz na pravé straně definován, takže to je taký ošetřeno.
9) To podle mě nestačí. Pokud  , tak ale stále může
, tak ale stále může  a co pak s tím? f(g(x)) není definováno. Přes tyto dvě podmínky by to mělo být ošetřeno.
a co pak s tím? f(g(x)) není definováno. Přes tyto dvě podmínky by to mělo být ošetřeno.
Offline
#4 04. 01. 2010 15:44
Re: Rychlokurz počítání elementárních limit funkcí
↑ halogan:↑ halogan:
Limity funkcií, ktoré nie sú konečné sa nedajú vonkoncom zistiť cez pravidlá o súčte, rozdiele, súčine a podiele. Sám hovoríš, pozor na neurčité výrazy. Dobre, nech
Idem použiť tvoj návod, keďže predpoklady sú splnené, pri výpočte limity funkcie  pre
pre  . Dostávam
. Dostávam 
Takže určite nie. Bolo by dobré venovať jeden odstavec práve nevlastným limitám, t.j. napr.:
ak g(x) ide k nule a rozobrať prípady.
Ad zložená funkcia. A prečo sa zaoberáme rovnicou  ? Je to vôbec nutné? Nás zaujíma správanie sa funkcie v okolí. Z vety platí
? Je to vôbec nutné? Nás zaujíma správanie sa funkcie v okolí. Z vety platí
Ak budeme uvažovať definičný obor  , potom zrejme
, potom zrejme 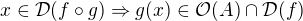 . Odtiaľ vyplýva, že ak
. Odtiaľ vyplýva, že ak  , potom
, potom
Zároveň ak  teda je veta je dokázaná a to s predpokladom
teda je veta je dokázaná a to s predpokladom  .
.
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#5 04. 01. 2010 15:55
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Rychlokurz počítání elementárních limit funkcí
↑ lukaszh:
1) Žádné ups, pravá strana není definovaná, takže aritmetiku nelze použít.
2) Tak nechť A nepatří do Df. Vezměme funkce jdoucí do nekonečna. g(x) = 1, f(y) = 1/(y-1)
G jde do jedné (A) a f nemá jedničku v def. oboru. Splňují tvé předpoklady. A nastává problém, protože složená funkce není nikde definovaná.
Offline
#6 04. 01. 2010 16:04 — Editoval lukaszh (04. 01. 2010 16:04)
Re: Rychlokurz počítání elementárních limit funkcí
↑ halogan:
1):-) Oups preto, lebo používam tvoje predpoklady. Ide mi o to, aby si odstránil rozšírenie R*, predpokladal existenciu iba vlastných limít. Vtedy to bude jednoznačné. Pod to treba napísať poznámku, že uvedené pravidlá sa nevzťahujú vo všeobecnosti pre nevlastné A,B (a teda pozor na neurčité výrazy)
2) Ale (f○g) v tomto prípade nemá žiadny hromadný bod v D, teda nemá význam sa zamýšľať nad pojmom limita ako takým.
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#7 04. 01. 2010 16:08
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Rychlokurz počítání elementárních limit funkcí
1) To je pak ale stejné, jako mé tvrzení :-)
2) Ale podle tebe ta limita existuje (resp. dle tebou upravené věty). Ta mnou napsána věta platí univerzálně a tento speciální případ odchytí už u podmínek.
Obě věty ku vzájemné radosti učitele i žáků používáme na analýze a nebyl s nimi problém :-)
Offline
#8 04. 01. 2010 16:17
Re: Rychlokurz počítání elementárních limit funkcí
Aritmetika limit funguje i pro nevlastní limity, pokud je daná výsledná početní operace definována. Např
Zcela korektně jsem sečetl limity a dobral se správného výsledku.
Jiný příklad:
Stejně jako v předchozím případě.
Viz např. zde, str. 18, Věta 1.4.17.
Offline
#9 04. 01. 2010 16:17
Re: Rychlokurz počítání elementárních limit funkcí
↑ halogan:
1) už som sa vyrozprával, bez komentára
2) ja som vetu nevyslovil. Len som napísal: z vety vyplýva. Nájdeš ju v ktorýchkoľvek serióznych skriptách. Samozrejme, nehádam sa s tebou, že to čo si napísal je zlé. Niekde sa dokonca uvádza len jedna jediná. Ja osobne som sa stretol s týmito troma. Nečakal som toľko rečí okolo :-) Dôkaz s využitím platnosti pridanej možnosti je v každom prípade uvedený.
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Rychlokurz počítání elementárních limit funkcí (TOTO TÉMA JE VYŘEŠENÉ)
