Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 20. 02. 2010 12:24
Průběh logaritmické funkce
Zdravim, potřebovala bych poradit s postupem, jak vypočítat průběh logaritmcké funkce.
f(x) = log3x + 1
Ve škole jsme brali snad všechny typy, až na tuto...
Určete:
D(f)
Průsečíky s osami
lokální extrémy
asymptota svislá
asymptota vodorovná
D(f) mi vyšel: (0,∞)
Potřebovala bych postup a pak už to snad půjde.
Díky moc všem za příspěvky.
Offline
- (téma jako vyřešené označil(a) nunik)
#2 20. 02. 2010 13:00
Re: Průběh logaritmické funkce
↑ nunik:
Definicny obor mas dobre :)
Z toho hned vyplyva, ze priesecnik s osou y neexistuje, lebo funkcia nie je v bode x=0 definovana. Priesecnik s osou x vypocitame tak, ze riesime rovnicu 0 = log3x + 1, tato rovnica riesenie ma (jedno, teda priesecnik s osou x je jeden).
Lokalne extremy funkcia nema, to ukazeme tak, ze vypocitame jej prvu derivaciu a zistime, preco sa nikdy nebude rovnat nule. Aby mohla mat funkcia v danom bode lokalny extrem, tak sa musi jej prva derivacia v tomto bode rovnat nule (nutna podmienka).
Vodorovna asymptota neexistuje, zvislou je os y, teda priamka x=0.
Toto vsetko prakticky okamzite vidno z grafu funkcie, ktory urcite odporucam si nakreslit :) Ak nevies ako na to, tak zacni s funkciou y = log x, to je rastuca zhora ani zdola neohranicena funkcia prechadzajuca bodom [1,0]. Dalej funkcia y = log3x je taka ista, iba je 3-krat "stlacena" v "horizontalnom" smere (v smere osi x). No a napokon nasa funkcia y = log3x + 1 je taka ista iba je cela posunuta o 1 hore v smere osi y.
Dufam ze som pomohol :)
Offline
#4 20. 02. 2010 14:13
Re: Průběh logaritmické funkce
nunik napsal(a):
↑ mikee:
Díky, určitě mi to pomůže.
Teď jsem ještě narazila na určení inverzní funkce a inflexních bodů.
Tak s tím asi taky sama nepohnu...
Inverzní body jsou tam, kde druhá derivace je nulová. Správně bys měla zjistit, že nulová není nikde, proto žádný inflexní bod není.
Inverzní funkce k logaritmu je exponenciála. Zbývá vyřešit, jak přesně bude vypadat. Máme



Teď to akorát formálně přeznačíme a dostáváme kýženou inverzní funkci: 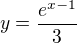 .
.
Mýlím se častěji, než bych chtěl. Pokud vám v mém příspěvku něco nehraje, neváhejte se zeptat.
Jsem stále mlád a je mi příjemnější tykání. :)
Offline
#6 20. 02. 2010 14:27
Re: Průběh logaritmické funkce
Asi by bylo dobré zjistit, jestli zápis log3x znamená logaritmus tří x nebo logaritmus x o základu 3. V prvním případě jestli se jako log označuje logaritmus dekadický, nebo přirozený.
Offline
#9 20. 02. 2010 14:55 — Editoval jelena (20. 02. 2010 14:59)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Průběh logaritmické funkce
↑ nunik:
Zdravím,
zde kolega Honza v tématech SŠ velmi srozumitelně vysvětluje, jak se to kreslí (+ odkaz na materiál úplně na závěr tématu) - odkaz + úvodní téma sekce VŠ - pozor však na zadání do Wolfram, je třeba také zadávat i def. obor (osobně bych v tomto případě nedoporučovala).
---
kolega Olin má nárok na puntiky za luštění zápisů, zdravím.
EDIT: postup nakreslení grafu popsal také ↑ mikee:, děkuji.
Offline
#11 20. 02. 2010 16:38
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Průběh logaritmické funkce
↑ nunik:
pokud je zadání funkce  , tak ani jedno z toho, co navrhuješ.
, tak ani jedno z toho, co navrhuješ.
(2,0) - ne, protože...
(1,1) - ne, protože...
----
OT: ...nemám v plánu vysloužit zablokování.
Offline
#12 20. 02. 2010 16:42 — Editoval Olin (20. 02. 2010 16:42)
Re: Průběh logaritmické funkce
↑ jelena:
Bohužel postup kreslení grafu, který navrhuje kolega mikee, se vztahuje k případu  , a tedy není správný (z tohoto hlediska).
, a tedy není správný (z tohoto hlediska).
Offline
#13 20. 02. 2010 16:56
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Průběh logaritmické funkce
↑ Olin:
Děkuji - přidavala jsem do editu také odkaz na postup od kolegy, jelikož mi nepřišlo správné opomenout, že ten postup je zde už jednou popsán (i když se váže k jinému zadání). Inverzní funkce od kolegy ↑ Oxyd: také se vztahuje k něčemu jinému. Postupy však jsou principiálně v pořádku (pokud se upřesní označení pro přirozený a dekadický logaritmus).
Ovšem autorka dotazu na nesrovnalosti v zápisech nijak nereaguje (ani v případě ↑ mikee:, ani v případě ↑ Oxyd:), tak bych to považovala za projev, že vnímá návrhy jako možné varianty práce s logaritickou funkci o základu větším, než 1, a že nemá problém s uzpůsobením návrhů pro případ logaritmu se základem (3).
Čemuž, samozřejmě, v tématech VŠ zcela věřím.
Offline
#17 20. 02. 2010 18:55
Re: Průběh logaritmické funkce
↑ zdenek1:
Díky.
Ta inverzní funkce, jak psal Oxyd je tedy dobře?
Offline
#19 21. 02. 2010 00:09
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Průběh logaritmické funkce
↑ zdenek1:
Zdravím, jen pro pořádek - postup pro inverzní funkci psal kolega ↑ Oxyd: (navíc já nepřehazuji, ale zautočím a "formálně přejmenovávám" až na závěr).
Offline
#21 21. 02. 2010 10:34
Re: Průběh logaritmické funkce
↑ zdenek1:
Ano týkají se této funkce.
A ten zbytek je jinak dobře?
Tak ten interval místo 1/3 má být 1? Nebo podle čeho se to určuje?
Offline

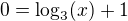
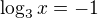

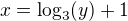

 a to je inverzní fce.
a to je inverzní fce. , tak intervaly monotónnosti nejsou dobře.
, tak intervaly monotónnosti nejsou dobře.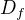 , tj.
, tj.