Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 20. 02. 2010 17:48 — Editoval BakyX (20. 02. 2010 17:50)
Kvadraticka rovnica
Máme danú kvadratickú rovnicu s parametrom:
Zisti hodnotu koeficientov a,b,c ak vieš, že:
a, b, c, t, x1, x2 sú celé čísla
a+b+c=1
ta*tb*tc=96
x1<x2
x2*2t^2=6
Zdvovodni, či existuje viacej riešení.
Prosim poraďte ako to spraviť fakt to neviem aj ked je to urcite lahke :D Dik
1^6 - 2^6 + 3^6 = 666
Offline
- (téma jako vyřešené označil(a) BakyX)
#2 22. 02. 2010 12:56
Re: Kvadraticka rovnica
Pokud správně rozumím těm podmínkám, kde se zdá, že někdy místo krát píšeš hvězdičku a někdy krát vynecháváš, pak (pokud si podmínky očísluji jako 1 až 5):
i) z podmínky 3) máme, že t je až na znaménko jednička nebo dvojka, protože 96 = 2^5 * 3
ii) z podmínky 5) pak máme, že x2 = 3 a t je až na znaménko jednička
iii) dosazením x2 za x máme z původní rovnice, že 3|c, ovšem z podmínky 3) máme, že c je rovno až na znaménko trojce
iv) opět z 3) máme, že a a b jsou pak mocniny dvojky a spolu s 2) máme jedinou dvojci takových mocnin: 4 a 8
v) z podmínky 2) pak ({a,b},c) = ({-4, 8}, -3)
vi) máme tedy dvě možnosti pro (a,b,c), což spolu se dvěma možnostma pro t dává čtyři možné rovnice, ale ani jedna z nich nemá kořen 3
Podle mě tedy tato úloha nemá řešení. Nejspíš není něco dobře v zadání. Doufám, že jsem (omylem) nepodal návod na nějakou soutěžní úlohu...
Offline
#3 22. 02. 2010 21:34
Re: Kvadraticka rovnica
Myslím že riešenie bude "nemá riešenie". Niesú to žiadne súťažné úlohy. Inak mam tu este jednu ale o dost zlozitejsiu ktora ma na 100% riesenie ale ja ho nepoznam :D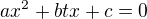
a, b, c, t sú reálne čísla.
x_1 je celé číslo.
x_2 je iracionálne číslo ktoré sa dá zapísať ako racionálne číslo
Teraz vlastnosti: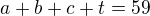
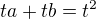

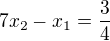
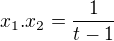
1^6 - 2^6 + 3^6 = 666
Offline
#5 23. 02. 2010 09:46 — Editoval musixx (23. 02. 2010 10:41)
Re: Kvadraticka rovnica
↑ Peter 002: Asi má na mysli, že x_2 je racionální, ale ne celé (EDIT: což je stejně informace, kterou vůbec nepotřebujeme, protože máme 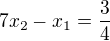 ).
).
Tyto příklady jsou pořád stejné. Dal jsem si ještě jednou tu práci, ale víckrát už to dělat nebudu. :-)
Není těžké ověřit, že  nevede k cíli, tedy z
nevede k cíli, tedy z 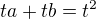 máme
máme  .
.
Z 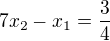 máme, že
máme, že 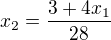 . Tedy musí jít o kvadratickou funkci
. Tedy musí jít o kvadratickou funkci 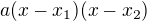 .
.
Vietovy vztahy spolu s 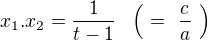 ,
,  a
a 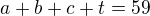 dávají, že
dávají, že  . No ale z předchozícho a tohoto jsme schopni napsat
. No ale z předchozícho a tohoto jsme schopni napsat  jako racionální lomenou funkci obsahující jedinou proměnnou
jako racionální lomenou funkci obsahující jedinou proměnnou  , která je celá, tedy
, která je celá, tedy  je racionální. Pak ale i
je racionální. Pak ale i  je racionální (protože
je racionální (protože 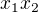 je racionální) a máme
je racionální) a máme


Teď už jen druhá mocnina 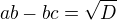 dá
dá ,
,
což je polynomiální rovnice pro  , kde se snadno vidí, že u nejvyšší mocniny
, kde se snadno vidí, že u nejvyšší mocniny 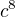 je koeficient 1 a absolutní člen je
je koeficient 1 a absolutní člen je 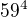 . Víme, že
. Víme, že  je racionální, tedy mnoho možností nemá (věta o racionálních kořenech polynomu s racionálními koeficienty). Jediné vyhovující je
je racionální, tedy mnoho možností nemá (věta o racionálních kořenech polynomu s racionálními koeficienty). Jediné vyhovující je  .
.
Pak ovšem  ,
, 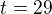 ,
, 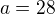 ,
,  a
a 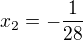 . EDIT2: Plus nezapomenout na zkoušku, protože jsme udělali jednu neekvivalentní úpravu -- je to ale snadné, stačí ověřit, že
. EDIT2: Plus nezapomenout na zkoušku, protože jsme udělali jednu neekvivalentní úpravu -- je to ale snadné, stačí ověřit, že 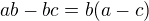 je kladné.
je kladné.
Offline
