Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » Kruznice, vepsani kruznice ctyruhelniku (TOTO TÉMA JE VYŘEŠENÉ)
#1 21. 02. 2010 11:57
Kruznice, vepsani kruznice ctyruhelniku
V kruznici se stredem O jsou dva na sebe kolme prumery AB a CD a tetiva AM, ktera protina prumer CD v bode K. Pro jakou hodnotu uhlu BAM lze ctyruhelniku OBMK vepsat kruznici ???
Predem dekuji za pomoc.
Offline
- (téma jako vyřešené označil(a) jelena)
#3 21. 02. 2010 12:44 — Editoval zdenek1 (21. 02. 2010 12:44)
Re: Kruznice, vepsani kruznice ctyruhelniku
↑ SirIndy:
Aby se dala vepsat kružnice, musí platit 
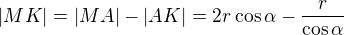
Rovnice 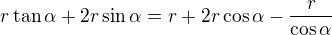 vede na
vede na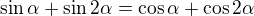
a po úpravách 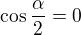 nebo
nebo 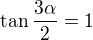
Kosinus ale nedává hodnotu z 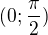 , takže zůstane
, takže zůstane
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#4 22. 02. 2010 14:14
Re: Kruznice, vepsani kruznice ctyruhelniku
↑ zdenek1:
Zdravim, podarilo se mi 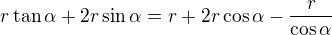 zdarne upravit na
zdarne upravit na 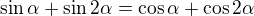 ale nevim, jak z toho dostat koreny, mohl bys poradit prosim?
ale nevim, jak z toho dostat koreny, mohl bys poradit prosim?
Offline
#5 22. 02. 2010 15:57
Re: Kruznice, vepsani kruznice ctyruhelniku
↑ SirIndy:
Použijeme 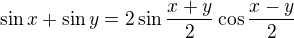 a obdobně pro kosinus
a obdobně pro kosinus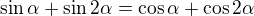
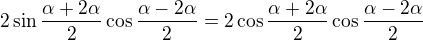
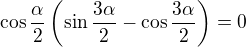
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
Stránky: 1
- Hlavní strana
- » Střední škola
- » Kruznice, vepsani kruznice ctyruhelniku (TOTO TÉMA JE VYŘEŠENÉ)
