Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Březnová limita III (TOTO TÉMA JE VYŘEŠENÉ)
#1 06. 03. 2010 17:43
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Březnová limita III
Pro  najděte limitu
najděte limitu .
.
Offline
- (téma jako vyřešené označil(a) BrozekP)
#2 08. 03. 2010 18:01
Re: Březnová limita III
Offline
#3 14. 03. 2010 21:23 — Editoval Marian (14. 03. 2010 21:25)
#4 04. 06. 2010 17:09 — Editoval Marian (04. 06. 2010 19:27)
Re: Březnová limita III
Úloha je již zde hodně dlouho a já stále nevím, zda-li někdo má snadnější řešení. Konečně, v tomto příspěvku bych chtěl dovést úvahy do finále. Aby se mi to podařilo (cestou, kterou jsem si vybral), dokážu jedno pomocné tvrzení, jehož důkaz spočívá na Abelově parciální sumaci aplikované na zbytky konvergentní nekonečné řady s komplexními členy.
Přistoupíme nejprve k formulaci
Tvrzení. Nechť jsou splněny následující podmínky:
(1) řada komplexních čísel  konverguje,
konverguje,
(2)  je monotónní posloupnost reálných čísel pro každé přirozené
je monotónní posloupnost reálných čísel pro každé přirozené  ,
,
(3) existuje konstanta  taková, že pro každé přirozené
taková, že pro každé přirozené  platí
platí  ,
,
(4) limita posloupnosti  pro libovolné fixní přirozené
pro libovolné fixní přirozené  (tj. mimo jiné m<n).
(tj. mimo jiné m<n).
Potom
Je samozřejmé, že podmínky tohoto tvrzení lze bez problémů aplikovat na situaci v mém předchozím příspěvku.
Offline
#5 04. 06. 2010 17:57
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Březnová limita III
Omlouvám se, zapomněl jsem na toto téma. Já jsem limitu vyřešil pouze za předpokladu, že existuje.
Z toho snadno vyjádřím L:
Když jsem na fórum tuto limitu dával, myslel jsem, že dokázat existenci už bude lehké, to jsem se zmýlil. Strávil jsem tím pak ještě dost času, ale už se mi to nepodařilo dořešit.
Tvůj důkaz jsem si prošel, několik kroků mi není jasných, ještě se zamyslím a případně zeptám. Také mi zatím není jasné, jak bys tvrzení aplikoval na tuto limitu.
Offline
#6 04. 06. 2010 18:48
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Březnová limita III
Už mi zbývá poslední nejasnost. V části 2:
Marian napsal(a):
a tedy platí také
Neměla by před tím být ještě limita 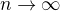 ? Také jsem si nevšiml, že bys toto někde dál použil. Můžeš to prosím podrobněji vysvětlit?
? Také jsem si nevšiml, že bys toto někde dál použil. Můžeš to prosím podrobněji vysvětlit?
Offline
#7 04. 06. 2010 19:11 — Editoval Marian (04. 06. 2010 19:26)
Re: Březnová limita III
↑ BrozekP:
Měla tam být limita, ale skutečně to nepotřebuju, takže tento kousek upravím v příští editaci (již opraveno). Dále ti nebylo jasné, jak aplikovat dokazované tvrzení na problém původní. Závěrem příspěvku #3 se vyskytuje limita ze součtu, kde horní mez sumace je obsažena netriviálně za znakem sumy. Položíme  a podobně
a podobně  ,
, 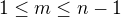 . Podmínka s monotonií je splněna a taktéž limita je nulová pro fixní m.
. Podmínka s monotonií je splněna a taktéž limita je nulová pro fixní m.
Hodně netriviální je situace, kdy posloupnost  nesplňuje podmínky uvedené v tvrzení výše. Potom se dokazuje podobné tvrzení mnohem obtížněji, nebo se dokázat třeba i nedá. Podobná tvrzení mají někdy zcela zásadní aplikace a důležitost.
nesplňuje podmínky uvedené v tvrzení výše. Potom se dokazuje podobné tvrzení mnohem obtížněji, nebo se dokázat třeba i nedá. Podobná tvrzení mají někdy zcela zásadní aplikace a důležitost.
Offline
#8 04. 06. 2010 21:17
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Březnová limita III
↑ Marian:
Díky za vysvětlení. Ta aplikace na limitu mi nebyla jasná zejména kvůli případu n=m, kdy by  nebylo definováno. Pak mi došlo, že si to třeba stačí malinko přeznačit (
nebylo definováno. Pak mi došlo, že si to třeba stačí malinko přeznačit ( ) a vše je hned jasné.
) a vše je hned jasné.
Offline
#10 08. 06. 2010 09:59
Re: Březnová limita III
↑ Tomas.P:
Odkud začíná úroveň "par excellence" ? Pohled na to je jistě relatvní. Jedinou cestou, jak se v tomto oboru rozvíjet, je studium - jako ostatně
v každém oboru. Výsledek závisí samozřejmě na úrovni zájmu i na talentu. Matematiku lze studovat jako samostatný universitní obor.
Nejpodstatnější je pochopit, o co v matematice obecně jde, což se universitní studenti oboru matematika dovědí hned v prvním semestru,
pak už by s pomocí vhodně seřazené literatury hypoteticky mohli vystačit se samostudiem.
Offline
#11 08. 06. 2010 13:10
Re: Březnová limita III
↑ Tomas.P:↑ Rumburak: Snad bych jen doplnil, že významný český matematik Vojtěch Jarník napsal článek o tom, jak studovat matematiku (máme-li o ni skutečný zájem). Tento článek je ke stažení volně zde ve formátu PDF (1,3 MB). Může sloužit jako inspirace.
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Březnová limita III (TOTO TÉMA JE VYŘEŠENÉ)
 ,
,  , výsledek
, výsledek  . Protože se to dá zapsat hezky jako konvergentní nekonečná geoemtrická řada
. Protože se to dá zapsat hezky jako konvergentní nekonečná geoemtrická řada  , řekl bych, že by to mohl být i výsledek pro obecné
, řekl bych, že by to mohl být i výsledek pro obecné 

 je možno psát
je možno psát

 ,
,  . Potom podle podmínky (4) dostáváme
. Potom podle podmínky (4) dostáváme

 volili fixní libovolné, je ho možné vždy zvolit dostatečně velké (ale stále fixní), že výraz
volili fixní libovolné, je ho možné vždy zvolit dostatečně velké (ale stále fixní), že výraz  bude libovolně malý (viz podmínka (1)). Odtud už plyne pravdivost tvrzení.
bude libovolně malý (viz podmínka (1)). Odtud už plyne pravdivost tvrzení.