Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » stejnoměrná konvergence funkčních posloupností (TOTO TÉMA JE VYŘEŠENÉ)
#1 05. 04. 2010 11:51
stejnoměrná konvergence funkčních posloupností
Dobrý den, prosím o pomoc se stejnoměrnou konvergencí funkčních posloupností.
Procházel jsem si teoretické materiály, ale u konkréních příkladů vždy narazím na nějaké komplikace/nejistoty.
Jako nejjednoduší se uvádí 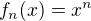 ; rozhoduji o stejnoměrné konv na intervalu
; rozhoduji o stejnoměrné konv na intervalu  ; limitní funkce
; limitní funkce 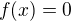 na M
na M
Pokud je interval M=<0,1>, limitní funkce f(x) na M je nespojitá -> st. konv. neplatí
Chci-li použít obecnější postup pro interval <0,1), tak derivací x^n zjišťuji, že x^n je na I <0,1) rostoucí na celém M a supremum leží na pravé straně intervalu v (1-) a tedy sup=1, ale jak se zjištěnými suprémy dále naložit?
Podmínkou stejnoměrné konvergence je  se musí rovnat nule.
se musí rovnat nule.
Očekával bych, že do výrazu  dosazuji za f_n(x) původní funkční posloupnost s takovou hodnotou x, v níž dostávám supremum na daném intervalu M a za f(x) dosazuji limitní funkci (v tomto případě f(x)=0).
dosazuji za f_n(x) původní funkční posloupnost s takovou hodnotou x, v níž dostávám supremum na daném intervalu M a za f(x) dosazuji limitní funkci (v tomto případě f(x)=0).
Použiji-li toto na úvodní 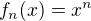 , pak dostávám
, pak dostávám  , což by ukazovalo na stejn. konv. Je tento postup správný?
, což by ukazovalo na stejn. konv. Je tento postup správný?
Je možné se spoléhat na to, že u stejn. konv f_n(x) budu-li přehazovat pořadí limit lim(n->∞) a lim(x->x0), pak mi vyjde vždy opravdu stejná hodnota pro jakékoliv libovolné x0 z intervalu stejnoměrné konvergence? nebo je možné, aby byla limitní funkce spojitá a zároveň měnila svoji hodnotu v závislosti na x0? (pak by snad nebylo možné měnit pořadí limit?)
Další příklad:
Mám-li funkční posl.  na
na  mi vychází
mi vychází 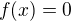 . Dále určuji supremum na I(0,1). Po 1.derivaci f_n1 a úpravách dostávám 1/2=x^n. Nechávám si funkci vykreslit a x=1/2 je opravdu vrchol. Nevadí, že jsem se nezbavil u x mocniny n? V jiných příkladech vycházelo x bez mocniny n.
. Dále určuji supremum na I(0,1). Po 1.derivaci f_n1 a úpravách dostávám 1/2=x^n. Nechávám si funkci vykreslit a x=1/2 je opravdu vrchol. Nevadí, že jsem se nezbavil u x mocniny n? V jiných příkladech vycházelo x bez mocniny n.
Použiji-li předchozí postup, pak  , což asi ale nebude správně, neboť z řešení úlohy vychází, že f_n1(x) není stejn. konv na M.<0,1>
, což asi ale nebude správně, neboť z řešení úlohy vychází, že f_n1(x) není stejn. konv na M.<0,1>
Věty říkají, že můžeme prokázat stejn. konv omezením fn_(x) shora jinou posloupností a_n, která konverguje k nule. Bylo by možně za tuto a_n uvažovat třeba f_na(x)=x^n-x^(4n)??
U příkladu  na
na  určuji opět
určuji opět 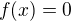 , ale zde mám potíž určit supremum - z derivace narůstají mocniny a neupravil jsem výraz dost šikovně, abych určil samotné x. Z vykreslení funkce ale vychází supremum nenulové, kladné. Jak zde mám dále pokračovat?
, ale zde mám potíž určit supremum - z derivace narůstají mocniny a neupravil jsem výraz dost šikovně, abych určil samotné x. Z vykreslení funkce ale vychází supremum nenulové, kladné. Jak zde mám dále pokračovat?
Mohu o stejn. konv rozhodnout jiným věrohodným způsobem, pokud nejsem schopen určit hodnotu přesně x, ve které má f_n(x) na daném int M supremum?
Omlouvám se za vychrlení řady dotazů, ale přiznávám, že s tímto tématem mám opravdu problém a opravdu rád bych to napravil. Hledal jsem sbírku řešených příkladů, ale ve většině materiálů uvedou tak leda dva/tři příklady na navzájem odlišné jevy a ve sbírkách pak už k jednotlivým příkladům píšou jen ano/ne, platí/neplatí.
Moc Vám děkuji za jakoukoliv ochotu a snahu o osvětlení. :-)
Offline
- (téma jako vyřešené označil(a) BrozekP)
#2 05. 04. 2010 12:03 — Editoval BrozekP (05. 04. 2010 12:54)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: stejnoměrná konvergence funkčních posloupností
Reaguji na první část do "Je tento postup správný?". Není správný. Za 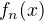 nedosazujeme rovnou supremum, ale
nedosazujeme rovnou supremum, ale 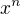 .
.
Pro každé n je  , takže pokračuji:
, takže pokračuji: ,
,
to znamená, že nekonverguje stejnoměrně.
Zeb napsal(a):
Je možné se spoléhat na to, že u stejn. konv f_n(x) budu-li přehazovat pořadí limit lim(n->∞) a lim(x->x0), pak mi vyjde vždy opravdu stejná hodnota pro jakékoliv libovolné x0 z intervalu stejnoměrné konvergence? nebo je možné, aby byla limitní funkce spojitá a zároveň měnila svoji hodnotu v závislosti na x0? (pak by snad nebylo možné měnit pořadí limit?)
To, že se tam objevila limita x->x0, je tím, že funkce f_n nabývá suprema na hranici množiny a je spojitá. To ale obecně vůbec takhle být nemusí. Existuje věta o záměně limit, jenže ta má v předpokladech právě stejnoměrnou konvergenci. Nemůžeme ji tedy použít pro dokazování stejnoměrné konvergence. Možná existuje i jiná věta o záměně limit, která by se někdy dala použít pro dokazování stejnoměrné konvergence, mě žádná ovšem nenapadá. Zde bychom ji ale určitě nemohli použít, protože zaměněním limit dostaneme jiný výsledek.
Zeb napsal(a):
Po 1.derivaci f_n1 a úpravách dostávám 1/2=x^n. Nechávám si funkci vykreslit a x=1/2 je opravdu vrchol.
x=1/2 je vrchol pouze pro n=1. Pro větší n bude vrchol v bodě daném rovnicí 1/2=x^n, čili  . Věty sice říkají, že když
. Věty sice říkají, že když  omezíme shora nějakou posloupností
omezíme shora nějakou posloupností  konvergující k nule, tak funkce konverguje stejnoměrně, ale tady nám to bude k ničemu, protože funkce stejnoměrně nekonverguje. Spočítejme limitu toho suprema (tahle funkce nabývá svého suprema v maximu, toho využijeme):
konvergující k nule, tak funkce konverguje stejnoměrně, ale tady nám to bude k ničemu, protože funkce stejnoměrně nekonverguje. Spočítejme limitu toho suprema (tahle funkce nabývá svého suprema v maximu, toho využijeme):![kopírovat do textarea $\lim_{n\to\infty}\sup_{x\in[0,1)}|f_n(x) - f(x)|=\lim_{n\to\infty}\sup_{x\in[0,1]}|x^n - x^{2n}|=\nl =\lim_{n\to\infty}\((2^{-\frac1n})^n -(2^{-\frac1n})^{2n}\)=\lim_{n\to\infty}\(\frac12-\frac14\)=\frac14\neq0$](/mathtex/27/27e8017e1d163a1723f726f4f76edd4f.gif)
z toho plyne, že posloupnost funkcí nekonverguje stejnoměrně. :
:
Tady stačí odhadnout supremum funkce 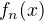 zdola funkční hodnotou v
zdola funkční hodnotou v  :
:
Příště by bylo lepší postupně klást otázky po jedné, takhle je to poměrně nepřehledné. Omlouvám se, pokud tam mám někde nesmysl, je toho hodně a kontrolovat se mi to nechce. Tak se kdyžtak ptej, kdyby něco nebylo jasné.
Offline
#3 05. 04. 2010 21:17
Re: stejnoměrná konvergence funkčních posloupností
↑ BrozekP:
Dobře, moc děkuji, určitě mi to pomohlo. :-)
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » stejnoměrná konvergence funkčních posloupností (TOTO TÉMA JE VYŘEŠENÉ)