Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » obecná rovnice tečny (TOTO TÉMA JE VYŘEŠENÉ)
#1 20. 02. 2008 19:36
- enclace.net
- Zelenáč
- Příspěvky: 22
- Reputace: 0
obecná rovnice tečny
zdravím
potřeboval bych helfnout, mám vypočítat obecnou rovnici tečny a normály ke grafu funkce
ale prosím s postupem, nemám žádný vzor a nějak mi to podle skript nejde spočítat
Offline
#3 20. 02. 2008 20:04
- enclace.net
- Zelenáč
- Příspěvky: 22
- Reputace: 0
Re: obecná rovnice tečny
↑ plisna:
jo pardom T[?,0]
Offline
#4 20. 02. 2008 20:19
Re: obecná rovnice tečny
x-ovou souradnici dopocitame z rovnice  , tedy mame dva body splnuji podminku:
, tedy mame dva body splnuji podminku: ![kopírovat do textarea $T_1 = [-1,0], \quad T_2 = [-2,0]$](/mathtex/55/55ea4a328e4949cf08ea1464715b1364.gif) . pro vypocet pouzijeme smernicovy tvar primky, ktery na konec prevedeme na pozadovanou obecnou rci.
. pro vypocet pouzijeme smernicovy tvar primky, ktery na konec prevedeme na pozadovanou obecnou rci.
vezmeme nejdrive bod ![kopírovat do textarea $T_1 = [-1,0]$](/mathtex/40/40beec6dc24e41b1720295d6db7e481d.gif) . uvazujme tedy tecnu ke grafu fce jakozto rovnici
. uvazujme tedy tecnu ke grafu fce jakozto rovnici  , kde k je smernice tecny a vypoctemeji pomoci derivace:
, kde k je smernice tecny a vypoctemeji pomoci derivace:  . nyni zbyva vypocitat q, provedeme dosazenim bodu dotyku do rovnice, tedy do rovnice
. nyni zbyva vypocitat q, provedeme dosazenim bodu dotyku do rovnice, tedy do rovnice  dosadime bod
dosadime bod ![kopírovat do textarea $T_1 = [-1,0]$](/mathtex/40/40beec6dc24e41b1720295d6db7e481d.gif) a vypocteme
a vypocteme 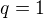 , tedy
, tedy  , obecna rce
, obecna rce 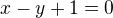 .
.
naprosto analogicky postupujeme pro druhy bod dotyku.
pro rovnici normaly musi platit, ze jeji normalovy vektor je kolmy na normalovy vektor tecny, tedy normalu hledame napriklad ve tvaru  , pricemz konstantu c opet vypocteme dosazenim bodu dotyku do rovnice.
, pricemz konstantu c opet vypocteme dosazenim bodu dotyku do rovnice.
(trochu jsem to u te normaly zrychlil, ale mame  , kolmy vektor muzeme zvolit tak, ze "prohodime" x-ovou a y-ovou souradnici a jedne navic zmenime znamenko, ja jsem tedy zvolil
, kolmy vektor muzeme zvolit tak, ze "prohodime" x-ovou a y-ovou souradnici a jedne navic zmenime znamenko, ja jsem tedy zvolil  )
)
Offline
#5 20. 02. 2008 20:24
- enclace.net
- Zelenáč
- Příspěvky: 22
- Reputace: 0
Re: obecná rovnice tečny
↑ plisna:
dík moc, už mi to došlo všecko
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » obecná rovnice tečny (TOTO TÉMA JE VYŘEŠENÉ)
 . otazkou zustava, v jakem bode ma byt sestrojena tecna. a nebo je bod obecny?
. otazkou zustava, v jakem bode ma byt sestrojena tecna. a nebo je bod obecny?