Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy ze základní školy
- » Konstrukce trojúhelníku (TOTO TÉMA JE VYŘEŠENÉ)
#1 01. 05. 2010 18:02
Konstrukce trojúhelníku
Dobrý podvečer,
ve škole jsem řešil úlohu,
se kterou si nevím rady.
Sestrojte rovnoramenný trojúhelník, jehož rameno měří 3 cm a poloměr kružnice vepsané je 1 cm.
Zkoušel jsem:
- kružnice se středem O a poloměrem 1 cm
- dvě rovnoběžné přímky (tečny)
- kolmice na přímky, tečna
a teď nevím co dál.
Prosím poraďte.
Děkuji
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
- (téma jako vyřešené označil(a) byk7)
#2 01. 05. 2010 18:14 — Editoval frank_horrigan (01. 05. 2010 18:32)
- frank_horrigan


- Příspěvky: 938
- Reputace: 31
Re: Konstrukce trojúhelníku
↑ byk7:
Zkusil bych vyuzit vztahu 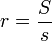 kde malé s je polovina obvodu. Poloměr znáš, hledáš tedy stranu, kterou vyjádříš z heronova vzorce, sestavíš rovnici, kde si položíš roven obsah z heronova vzorce a obsah vyjádřený z poloměru vepsané kruřnice. Je to brainstorming, nevim jestli to půjde, ale skusím to takto spočítat :)
kde malé s je polovina obvodu. Poloměr znáš, hledáš tedy stranu, kterou vyjádříš z heronova vzorce, sestavíš rovnici, kde si položíš roven obsah z heronova vzorce a obsah vyjádřený z poloměru vepsané kruřnice. Je to brainstorming, nevim jestli to půjde, ale skusím to takto spočítat :) //heron
//heron // obsah ze vzorce pro vepsanou
// obsah ze vzorce pro vepsanou
Z toho možná půjde vyjádřit a :)
Vychází mi (po prohnání strojem kořeny -10, 0 a +10) -> záporné a nulové strany asi ne :), zkus to dosadit, zda to vyjde, nejak se mi to nezdá
The only thing worse than being wrong is staying wrong
Sun Tzu - The Art of War
Offline
#4 01. 05. 2010 18:41 — Editoval frank_horrigan (01. 05. 2010 18:42)
- frank_horrigan


- Příspěvky: 938
- Reputace: 31
Re: Konstrukce trojúhelníku
↑ byk7:
Ještě jeden nápad ("prasárna"): Kruznice o poloměru máš - budoucí kruznice vepsana. Sestroj si "průměr" - maximální možnou tetivu (nevzpomenu si jak se tomu říká). Na bodech společných průmeru a kružnici ved kolmice -tečny. Ty se protnou, z vrcholu veď kružnici o r = 5. To budou Ostatní dva vrcholy. Nevím, prijde mi to jako prasárna, ale možná to projde :) To počítání bych bez stroje (wolframu) nedal, ani s beznou kalkulackou :)
The only thing worse than being wrong is staying wrong
Sun Tzu - The Art of War
Offline
#5 02. 05. 2010 12:11
Re: Konstrukce trojúhelníku
↑ frank_horrigan: ale ty tečny se neprotnou, protože jsou to rovnoběžky
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#6 02. 05. 2010 12:44 — Editoval frank_horrigan (02. 05. 2010 13:18)
- frank_horrigan


- Příspěvky: 938
- Reputace: 31
Re: Konstrukce trojúhelníku
↑ byk7:
Aha, no jo... pravdu máš, to mi nedoslo... Jeste mám jeden nápad: ten průměr máš, sestroj si jeste jeden, kolmý. Na jednom konci kolmici - tečnu (budoucí strana c. Druhý konec protáni, tam "nekde" bude lezet vrchol C. Sestoj tecny, tak, aby se protnuly na té prodlouzené úsečce. Jedna dvojice tečen bude mít velikost 3... Je to jenom nápad, myslim si, ze uvazuju správným smerem, jeste domyslet "elegantneji" ten jak udelat ty tecny o velikosti 3. Dotek s vepsanou kruznicí by měl být u rovnor. na ose strany C - tedy vzdalenost AT a BT by mela byt stejná (T je dotek strany s kruznici)
Uz to mám, stacilo si namalovat obrázek. Vyuzijeme podobnost trojúhelníků. Vezmi si, ze máš pravoúhlý troúhelník o odvesnách 2r a r, vypočítej přeponu. "Velkou" přeponu máš zadanou, stačí spočítat odvěsny, a sestrojíš trojúhelník :)
The only thing worse than being wrong is staying wrong
Sun Tzu - The Art of War
Offline
#7 02. 05. 2010 13:41
- frank_horrigan


- Příspěvky: 938
- Reputace: 31
Re: Konstrukce trojúhelníku
↑ byk7:
Zkusím to shrnout, asi je v tom pěknej bordel, ted:
1) v, S, 1cm //budoucí vepsaná
2) KL, |KL| = 2cm; K,L je prvkem v, S je prvkem KL // vertikální průměr
3) XY, XY je kolmá KL, S je prvkem KL //horizontální průmer
4) p, p je rovnoběžná s XY, K je prvkem p //tečna, strana c
5) q, q je rovnoběžná s KL, X je prvkem q
6) R, R je průnik p a q
7) Prav. trojúhelník RKL
RK = r = 1
KL = 2r = 2
RL = 
3: sqrt(5) = 1 : |AK| = 2: |KC|
Poměr podobnosti přibližně 1,34
8) AK, |AK| = 1 * 1.34 = 1.34
9) KC, |KC| = 2* 1.34 = 2.68
10) k, k(K, |KA|)
11)B, B je prunik p a k
12) troj ABC
Snad je to k pochopení :)
The only thing worse than being wrong is staying wrong
Sun Tzu - The Art of War
Offline
#8 02. 05. 2010 14:43
- frank_horrigan


- Příspěvky: 938
- Reputace: 31
Re: Konstrukce trojúhelníku
V kazdém případě mi tato uloha prijde jako zajimava, navrhuji přesunutí do sekce Zajímavé úlohy :)
The only thing worse than being wrong is staying wrong
Sun Tzu - The Art of War
Offline
#9 06. 05. 2010 14:35
Re: Konstrukce trojúhelníku
To frank_horrigan
Výpočet je nějaký divný.
Tak jak je úloha zadána nemá řešení (a musí být větší než 3.33019 cm)
Jinak pro základní školy docela dobrý.
Výpočet vede na algebraickou rovnici 3.řádu a konstrukce pravítko kružítko tedy nevím jak.
Offline
#11 06. 05. 2010 14:54
- frank_horrigan


- Příspěvky: 938
- Reputace: 31
Re: Konstrukce trojúhelníku
↑ Honzc:
Prave proto, ze z toho vypadla kubicka rovnice, a jeji koreny -10, 0 a +10 se mi to zdalo nejaky divny, a pro zakladni (ono, co si budeme povidat) ani pro stredni je ten vypocet nepouzitelny, zkusil jsem na to jit geometricky a myslim,ze ten postup ma smysl a logiku - pres podobnost. A (zakladna) bude urcite vetsi nez 3,33 :) Nemám tady přislusné vybavení (jsem prece jen "jenom" finančník), ale z nacrtku plyne, ze ta uloha reseni ma :) A fakt je, ze pro zakladku je to na hrane, mozna tak do olympiady, sice jsem pouzil kostrukci ktere se na ZS uci (aspon myslim, heronuv vzorec jsem taky myslel ze v devaty probiraj), a jenom se u toho musi premyslet :)
Pokud ses opačného názoru, můzeš mi ukázat (početne, nebo obrázkem) co přesně na tom nejde sestrojit?
The only thing worse than being wrong is staying wrong
Sun Tzu - The Art of War
Offline
#14 06. 05. 2010 17:45
- frank_horrigan


- Příspěvky: 938
- Reputace: 31
Re: Konstrukce trojúhelníku
Dobrá, kluci, dobra :) Takze konketne na tyto rozmery (respektive jejich pomer) neni reseni, fajn :) Spocitat si to nedokazu (nebo mozna dokazu, ale jsem na to moc velkej lempl), takze vam budu verit :)
The only thing worse than being wrong is staying wrong
Sun Tzu - The Art of War
Offline
#15 29. 07. 2010 09:05 — Editoval BakyX (30. 07. 2010 14:33)
Re: Konstrukce trojúhelníku
↑ frank_horrigan:
(Prispievam do vyriešenej témy - viem to)
Mám pocit, že ten tvôj postup je aj tak zlý. Tie 2 trojuholníku totiž nie sú podobné. Dá sa to jednoducho dokázať. Pravouhlý trojuholník s odvesnami x, 2x má vždy rovnaké uhly. Rovnoramenný trojuholník rovnaké uhly vždy nemá
1^6 - 2^6 + 3^6 = 666
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy ze základní školy
- » Konstrukce trojúhelníku (TOTO TÉMA JE VYŘEŠENÉ)

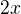



![kopírovat do textarea $\sqrt{\frac{1-\cos{\alpha}}{1+\cos{\alpha}}}=\frac{1}{x} \nl \frac{1-\frac{x}{3}}{1+\frac{x}{3}}=\frac{1}{x^2} \nl \frac{3-x}{3+x}=\frac{1}{x^2} \nl x^3-3x^2+x+3=0 \nl x_1=1-\sqrt[3]{1-\frac{\sqrt{57}}{9}}-\frac{2\cdot\sqrt[3]{9\cdot{\(9-\sqrt{57}\)}^2}}{3\cdot\(9-\sqrt{57}\)} \nl x_{2;3}\in\mathbb{C}\rightarrow\mathrm{netreba\,\,uvazovat} \nl x<0 \Rightarrow \mathrm{nema\,\,reseni}$](/mathtex/e8/e8ab192a685010e4c5bbea5fc232126d.gif)

 - což nelze
- což nelze