Matematické Fórum

halogan · 28. 05. 2010 18:17

Dobrý podvečer přeji,

mám tu následující řadu:

A mám vyšetřit její konvergenci.

1) Vzhledem k tomu, že sudé členy budou nulové, jsem si řadu přepsal jako

$\sum_{n = 1}^{\infty} (-1)^{n + 1} \text{tan} $\frac{1}{2n - 1}$ \frac{3 (2n - 1)^2 + 1}{2 (2n - 1)^2}$

Teď je otázka, co s tím.

1) Jít na to přes implikaci AK => K. To už od pohledu nefunguje, protože poslední faktor se chová jako konstanta, tangens se chová jako argument, takže to celkově vypadá jako 1/kn, což diverguje.

2) Zbývá jen Leibniz (vzhledem k mým omezeným možnostem) a má se to přes něj i řešit. Teď jak ukázat, že členy klesají?

a) Derivovat a dostat něco hnusného.

b) Dát to do nerovnosti a dostat něco neporovnatelného.

c) Suše říci, že když b_n (to je a_n bez toho alternujícího faktoru) jde k nule a jsou to samé kladné hodnoty, tak kdyby to neklesalo, tak by se to muselo "vlnit", ale to bychom měli nekonečné množství lokálních extrémů, které ale v té derivaci nemohou nastat, protože to bude polynom druhého stupně (a nějaké nenulové složky jako je tangens kolem nuly nebo kosínus kolem nuly).

---

Jak jinak to vysvětlit?

Děkuji.

Marian · 28. 05. 2010 20:02 — Editoval Marian (28. 05. 2010 20:17)

↑ halogan: Chce to jen drobný vtípek. Stačí upravit racionální funkci do tvaru

$R(n):=\frac{3(2n-1)^2+1}{2(2n-1)^2}=\frac{3}{2}+\frac{1}{2(2n-1)^2}.$

Odtud je vidět, že racionální funkce $R(n)$ je kladná a klesající. Stejně tak je klesající a kladná funkce tan(1/(2n-1)). Proto jejich součin je opět kladná klesající funkce. Odtud z Leibnizova kritéria plyne bezprostředně konvergence předložené nekonečné řady.

Poznámka. Zapisuj racionální argumenty funkcí pro jistotu do závorky. Tvůj zápis potom může být matoucí. Dále bych chtěl upozornit na drobnost. Původní řada s členem 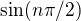$\sin (n\pi /2)$ a tebou transformovaná řada s členem 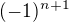$(-1)^{n+1}$ nejsou stejné nekonečné řady. Důvod je v definici nekonečné řady. Pokud chceme pracovat seriózně s nekonečnou řadou, je zapotřebí ji vnímat jako posloupnost částečných součtů (a tyto nejsou stejné). Ovšem na konvergenci to vliv mít nebude. Dokonce nebude mít tvé počínáná vliv ani na součet nekonečné řady. Takovému jevu se říká dilution of the infinite series. Pokud se chceš přesvědčit, že vliv na konvergenci skutečně nemá, podívej se na Větu 6, str. 51. Přečti si také poznámku nad větou a poznámku pod čarou (vše na téže stránce).

halogan · 28. 05. 2010 20:10

↑ Marian:

Ono i bez toho převodu je vidět, že ke své limitě jde zeshora, takže klesá. Při té úpravě jsem měl v hlavě předchozí řadu (s arctan n), a byl jsem tím pádem přesvědčen, že ten tangens roste :-) Stejně na té úloze bude asi stěžejní vůbec si uvědomit, jak přepsat tu řadu.

Přestávám počítat a jdu se věnovat něčemu jinému.

Jako vždy děkuji pěkně a přeji příjemný zbytek týdne.

---

Reakce na poznámku:

Děkuji za upozornění. Argument byl v závorce, ale nebyl vytexován. Vycházel jsem z toho, že pokud je nekonečno opravdu nekonečno, tak že když budu postupovat trochu rychleji, tak toho tolik nepokazím. S tím jsem tiše doufal, že na součet to nebude mít vliv. Děkuji za odkazy.

Matematické Fórum

#1 28. 05. 2010 18:17

Konvergence alternující řady

#2 28. 05. 2010 20:02 — Editoval Marian (28. 05. 2010 20:17)

Re: Konvergence alternující řady

#3 28. 05. 2010 20:10

Re: Konvergence alternující řady

Zápatí