Matematické Fórum

BakyX · 30. 05. 2010 22:04

Dobrý deň. Mám veľký problém s touto úlohou - nemôžem sa pohnuť:

Odvoďte vzorec pre výpočet obsahu kruhu s polomerom r.

Ďakujem za pomoic

Krezz · 30. 05. 2010 22:08 — Editoval Krezz (30. 05. 2010 22:09)

http://cs.wikipedia.org/wiki/Kru%C5%BEnice
ja myslim ze je to tam velmi dobre popsano z ceho tohle vychazi :)
prepsat do napr z analytiky do urciteho integralu uz neni tak tezky.

Rumburak

↑ BakyX:

Označme 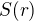$S(r)$ obsah kruhu o poloměru $r$ a určeme derivaci funkce $S$ .
Rozdíl $S(r+h)\, -\, S(r)$ pro $h > 0$ blízké nule je roven obsahu jakéhosi mezikruží o šířce $h$ . Jeho obsah se bude málo lišit
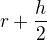od obsahu obdélníka, jehož kratší strana má délku $h$ a delší strana $2 \pi (r + \frac{h}{2})$ . Číslo $r + \frac{h}{2}$ , které v tomto výraze figuruje,
jsme získali jako aritmetický průměr z poloměrů větší a menší kružnice, které to mezikruží ohraničují, takže $2 \pi (r + \frac{h}{2})$ je délka
příslušné "střední" kružnice v tomto mezikruží.

Takže $S'_{+}(r) \,=\,\lim_{h \to 0_{+}}\,\frac {S(r+h)\, -\, S(r)}{h}\,=\,\lim_{h \to 0_{+}}\,\frac {2 \pi (r + \frac{h}{2})\,h}{h}\,=\,\lim_{h \to 0_{+}}\,\,2 \pi (r + \frac{h}{2}) \,=\,2\pi r$ .

Obdobným způsobem a se stejným výsledkem určíme derivaci zleva. Integrací pak obdržíme

$S(r) \,=\, S(0)\,+\,\int_0^rS'(\rho)\,\text{d} \rho \,=\, S(0)\,+\,\int_0^r 2\pi \rho\,\text{d} \rho\,=\,S(0)\,+\, \pi r^2$ ,

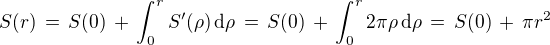kde zřejmě S(0) = 0.

EDIT.
Toto byl takový "fyzikální" způsob výpočtu (doufám, že se tímto označením nedotknu kolegů fyziků). Seriosnější po matematické stránce
by bylo spočítat integrál

$\frac {1}{2}S(r)\,=\,\int_{-r}^r \sqrt{r^2 \,-\,x^2}\,\text{d} x$ ,

(obsah plochy omezené grafem funkce a osou x), ale výpočet integrálu tohoto tvaru se na SŠ , myslím, ještě neprobírá.

Matematické Fórum

#1 30. 05. 2010 22:04

Dvôkaz vzorca pomocou určitého integrálu

#2 30. 05. 2010 22:08 — Editoval Krezz (30. 05. 2010 22:09)

Re: Dvôkaz vzorca pomocou určitého integrálu

#3 31. 05. 2010 10:32 — Editoval Rumburak (31. 05. 2010 11:33)

Re: Dvôkaz vzorca pomocou určitého integrálu

Zápatí