Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 01. 06. 2010 18:17
exponenciální rovnice..4tý typ
prostě si nemožu zaboha vzpomenout jak s toho ven..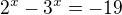
dyž to podělím  tak si nepomožu bo zůstane u
tak si nepomožu bo zůstane u 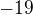
je mi jasný že výsledek má být 3 ale jak se k tomu dostanu? (komplexních čísel -> logaritmů ze záporných čísel se nebojím :) )
(: SMILE :)
Offline
- (téma jako vyřešené označil(a) graviton)
#2 01. 06. 2010 18:25
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: exponenciální rovnice..4tý typ
Tohle asi nepůjde analyticky vyřešit jinak než kořen uhádnout a dokázat, že neexistuje jiný.
Offline
#5 03. 06. 2010 13:47
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: exponenciální rovnice..4tý typ
Zkus si to nakreslit. Než s tím začneš, tak si to přehoď: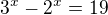
To ti tedy říká, že hledáš takové x, kdy rozdíl funkčních hodnot těchto dvou funkcí je roven 19. Už jsi ho našel a chceš vědět, že je jediné.
Dalo by se to odhadnout z toho, že ta první funkce roste mnohem rychleji než ta druhá. Pokud tedy tušíme, že by mohl být jediný, můžeme se přesunout k důkazu.
Abys mohl tvrdit, že to x existuje jen jediné, tak to můžeš udělat třeba tak, že ukážeš, že funkce 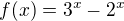 je ryze monotónní (nebo alespoň na určitých intervalech). Potom bude i prostá, takže pro každé číslo z H(f) [třeba A] najdeš právě jedno x, které splňuje
je ryze monotónní (nebo alespoň na určitých intervalech). Potom bude i prostá, takže pro každé číslo z H(f) [třeba A] najdeš právě jedno x, které splňuje 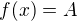 .
.
A ryzí monotonie se ukáže celkem snadno.
Offline
#6 03. 06. 2010 14:38 — Editoval Krezz (03. 06. 2010 14:45)
Re: exponenciální rovnice..4tý typ
↑ graviton:
27-8 je 19 ne -19, musel bys to vynasobit prvni -1 az potom by to davalo smysl :) Navic ja bych to ani nedelal, proc?
tady uz je zhrejme cemu se asi x bude rovnat, mame totiz levou i pravou stranu naprosto stejnou, na levo jsou v exponentu x a vpravo jsou to jen trojky, zda je to jedine reseni uz vysvetlil kolega. S tim nakresem je to opravdu docela jasne, navic pokud si nakreslis primku ktera protina exponencialcni fci a tato primka je rovnobezna s osou x tak je to jasny ze bude pouze jedno.
Offline
#7 04. 06. 2010 05:48 — Editoval Honzc (04. 06. 2010 09:14)
Re: exponenciální rovnice..4tý typ
↑ Krezz:
"navic pokud si nakreslis primku ktera protina exponencialcni fci a tato primka je rovnobezna s osou x tak je to jasny ze bude pouze jedno"
ovšem to není pravda, přímka musí být rovnoběžná s osou y.
To, že řešení je jedno se dá ukázat i takto:
Když si představíme grafy funkcí y=3^x a y=2^x, tak je zřejmé, že:
a) oba procházejí bodem [0,1]
b) pro x>0 roste y=3^x rychleji, než y=2^x
c) děláme-li nyní rovnoběžky s osou y v nějakém bodě x (X>0), je zřejmé, že existuje pouze
jediné x, ve kterém je rozdíl funkčních hodnot (délka úsečky) roven nějakému číslu, u nás
číslu 19
Offline



