Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Základní škola
- » Konštrukcia rovnoramenného trojuholníka (TOTO TÉMA JE VYŘEŠENÉ)
#1 07. 06. 2010 15:45 — Editoval BakyX (08. 06. 2010 16:09)
Konštrukcia rovnoramenného trojuholníka
Dobrý deň. Rozmýšlal som o konštrukcii rovnoramenného trojuholníka pomocou kružnice vpísanej a ramena. Môj postup
Z rovnoramenného trojuholníka spravím rovnoramenný lichobežník zložený z 3 zhodných rovnoramenných trojuholníkov. To spravím v oboch polrovinách. Každému trojuholníku vpíšem kružnicu. Spojím stred týchto vpísaných kružníc do šesťuholníka. Tento šesťuholník bude pravidelný zo stranou dĺžky 2r. Keďže poznám "r" tak ho môžem narysovať. Nájdem všetky stredy strán tohto šesťuholníka. Takto spojím všetky stredy strán, ktoré sú rovnobežné. Ich Priesečník je bod C. Teraz spravím kružnicu s polomerom "a" z bodu C. Jednotlivé úsečky, ktoré spájaju stredy rovnobežník strán v šesťuholníku predĺžim a tam, kde sa mi pretnú s kružnicou s polomerom "a", sú body A,B.
Je toto riešenie dobré ? Ďakujem za pomoc
EDIT: TAK ten môj postup je zlý. Thx Spybot
1^6 - 2^6 + 3^6 = 666
Offline
- (téma jako vyřešené označil(a) BakyX)
#2 08. 06. 2010 00:12
Re: Konštrukcia rovnoramenného trojuholníka
Zdravim, podla mojho nazoru Tebou uvadzane riesenie bude fungovat len v pripade, ze je ten trojuholnik rovnostranny.
Totizto iba vtedy bude platit, ze strana toho sestuholnika bude 2r.
Vezmime si lichobeznik, z ktoreho navrhujes vychadzat a rozlozme ho na kosodlznik a rovnoramenny trojuholnik. Tento kosodlznik sa sklada z dvoch ronoramennych trojuholnikov, inak povedane kratsia uhlopriecka je rovnakej velkosti ako bocna strana b. Teraz, aby bola vzdialenost stredov kruznic vpisanych tymto trojuholnikom rovna 2r, musia stredy lezat na jednej priamke, teda prva kruznica sa musi uhlopriecky (a spolocnej strany trojuholnikov) dotykat v rovnakom bode ako druha kruznica.
Vpisane kruznice rysujeme ako priesecnik osi uhlov. Vezmime si uhly BAD a BCD. Aby kruznice naozaj lezali na jednej priamke, musi byt os uhla BAD zaroven osou uhla BCD - tato spolocna os musi byt uhloprieckou kosodlznika, uhloprieckou, pre ktoru plati, ze rozpoluje uhly. To ale v kosodlzniku uhlopriecka nerobi (v kosostvorci ano). Teda podla mna nedospejeme tymto postupom k spravnej konstrukcii.
Geometria, ci matematicke vyjadrovanie nie su mojimi silnymi strankami, navyse som tento prispevok pisal po castiach, tak snad je zrozumitelny.
A este by som chcel dodat, ze ak mam pravdu, velmi by ma zaujimalo skutocne riesenie tejto ulohy (pre udaje, pre ktore je mozne trojuholnik narysovat). Uz som nad nou co-to presedel.
Offline
#4 08. 06. 2010 16:13
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Konštrukcia rovnoramenného trojuholníka
↑ BakyX:
V mailu jsi mi psal, že známe poloměr kružnice opsané. Správně má být tedy vepsané?
Offline
#6 08. 06. 2010 16:55
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Konštrukcia rovnoramenného trojuholníka
Nic mě nenapadá. Ani spočítat to asi nepůjde nijak dobře - základna vychází ,
,
kde a je délka odvěsny a r poloměr kružnice vepsané.
Offline
#8 08. 06. 2010 17:37
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Konštrukcia rovnoramenného trojuholníka
↑ BakyX:
Jistě, že dalo (spíš bych pak mluvil o rovnoběžníku). Ale nevidím, že by to k něčemu vedlo.
Offline
#10 10. 06. 2010 13:47
Re: Konštrukcia rovnoramenného trojuholníka
Ďalší pokus:
Náčrt:
Neviem spraviť cez PC tak len napíšem.
Načrtnem trojuholník ABC. Načrt osy ohlov ABC a BAC. Priesečník, čiže stred kružnice vpísanej, označím S1. Načrtnem polomer kružnice, ktorý pretne stranu BC. Bod, v ktorom ju pretne, označím D. Predĺžím os uhla ABC od vrcholu B dole a stranu BC od vrcholu B dole. Na predĺženej strane BC, teda na polpriamke CB označím bod E tak, aby EB=BD. Z bodu E urobím kolmú priamku smerom doprava. Na tejto priamke označím bod S2 tak, aby S2E=r, kde r je polomer kružnice vpísanej. Bod S2 by mal byť zároveň priesečníkom predĺženej osy uhla ABC a kolmej priamky cez bod E. Na predĺženej úsečke BC zvolím bod F tak, aby FB=BC. Spravim kružnicu z polomerom "r" a stredom v bode S2. Nájdem bod G tak, aby trojuholník ABC bol zhodný s trojuholníkom FGB.
Už len zistiť, či daná veci, čo som napísal, platia. Čo myslíte ?
1^6 - 2^6 + 3^6 = 666
Offline
#11 10. 06. 2010 13:54 — Editoval Cheop (10. 06. 2010 13:55)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Konštrukcia rovnoramenného trojuholníka
↑ BakyX:
Na první pohled se mi to nezdá (jedná se o bod S2) - podle mne nebude ležet na ose úhlu beta
Ale jdu to spočítat a načrtnout
Nikdo není dokonalý
Offline
#12 10. 06. 2010 13:58
Re: Konštrukcia rovnoramenného trojuholníka
Ani mne veľmi. Ja to zjednoduším.
Mame daný trojuholník ABC, ktorý je rovnoramenný. Existuje taký trojuholník BXY tak, že je zhodný s trojuholnikom ABC tak, že X leží na polpriamke CB a stred jeho vpísanej kružnice leží na osi uhla ABC
1^6 - 2^6 + 3^6 = 666
Offline
#13 10. 06. 2010 20:48 — Editoval byk7 (12. 07. 2010 09:23)
Re: Konštrukcia rovnoramenného trojuholníka
↑ BrozekP:
myslím, že to jde jednodušeji:
a - rameno
r - poloměr kružnice vepsané
2x - základna
alpha - úhel při základně
musí platit: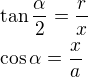
upravím:

Edit: jak se tak dívám, ten kořen moc hezky taky nevyjde, omlouvám se
Edit2: a je to to stejné, jak co máš ty
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
Stránky: 1
- Hlavní strana
- » Základní škola
- » Konštrukcia rovnoramenného trojuholníka (TOTO TÉMA JE VYŘEŠENÉ)
![kopírovat do textarea $\Large 2x=\frac{\,\,2\sqrt[3]{a^3+\(3\sqrt{3}\)\cdot\sqrt{-a^4r^2+11a^2r^4+r^6\,\,}-18ar^2\,\,}\,\,}{3}-\frac{6r^2-2a^2}{\,\,\sqrt[3]{a^3+\(3\sqrt{3}\)\cdot\sqrt{-a^4r^2+11a^2r^4+r^6\,\,}-18ar^2\,\,}\,\,}\nl+\frac{\,\,2a\,\,}{\,\,3\,\,}$](/mathtex/36/3603066e22948d7db93aa642f4292b28.gif)