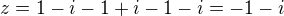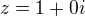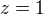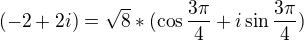Matematické Fórum

lucik.kicul

Potřebovala bych najít chybu v těchto příkladech:
imaginární část komplexního čísla z=1-i+i^2-i^3-i^4-i^5 je rovna číslu má to vyjít -1, ale mně to tak nevychází, můj postup:
z=1-i-1-(-i)-1-i=1-i-1+i-i=vyjde mi -i

2. příklad: imaginární část komplexního čísla z=1+i+i^2+i^3+i^4+i^5+i^6 je rovna číslu výsledek má být 1,
můj postup:
z=1+i-1-i+1+i-1=mně vychází i

3. příklad: imaginární část komplexního čísla z=1-i^3-i^5-i^7-i^9 je rovna číslu jejich výsledek 0
můj postup:
z=1-(-i)-i-(-i)-i=1+i-i+i-i=mně vychází 1

Děkuju

Mr.Pinker · 12. 06. 2010 08:48

$z=1-i-1+i-1-i=-1-i$
tudíž když se koukneš tak to opravdu vychází mínus jedna

lucik.kicul · 12. 06. 2010 08:49

↑ Mr.Pinker:
děkuju už to vidím =)

lucik.kicul · 12. 06. 2010 08:52

podívate se mi prosím i na ty ostatní příklady, víc očí víc vidí

Mr.Pinker

↑ lucik.kicul:
jistě ale imaginární část je jen to co je před i to že tam je to i určuje že je to ta imaginární část např.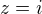
$z=i$
tak imaginární část je rovna jedné
jinak postup u příkladů máš dobře

lucik.kicul · 12. 06. 2010 08:58

děkuju moc a u toho třetího příkladu? když mi vyšla 1, tak z=1 je nula?

Mr.Pinker · 12. 06. 2010 09:02

jistě jelikož by se to mohlo zapsat takto
$z=1+0i$
kde koeficient bude nula před i ale jak sama víš cokoliv krát nula je nula
tudíž to stačí napsat tak to
$z=1$
komplexní čísla u níž je imaginární část nula sou prakticky reálná čísla

lucik.kicul · 12. 06. 2010 09:04

Opravdu děkuju moc za pomoc =), dneska to asi nebude naposled =)

lucik.kicul · 12. 06. 2010 11:10

Mám dotaz.
mám příklad: reálná část komplexního čísla (-2+2i)^6 je rovna číslu:
vím, jak to vypočítat, ale závěry mi nejdou,
dopočetla jsem se k moivreově větě:(\sprt8)^6*(cos3\sprt2+isin3\sprt2)=8^3.... výsledek má vyjít 0, to mám snad cos odečíst od sinusu, aby mi vyšla nula? Můžu to tak udělat?
Děkuju

Mr.Pinker · 12. 06. 2010 11:19

špatně si to pochopila
ty části sou právě skvěle vidět na goniometickém tvaru
sin*abolutní hodnota je imaginarní část a cos*absolutní hodnota je reálná část tudíž ti stačí vynásobit aboslutní hodnotu s velikostí toho cosinu a máš reálnou část

lucik.kicul · 12. 06. 2010 11:51

↑ Mr.Pinker:
takto: cos3\sprt 2*\sprt8 ? Jak mi z toho vyjde nula? Ty konce mi moc nejdou. Prosím trpělivost
Jinak ten postup mám dobře?

Mr.Pinker · 12. 06. 2010 11:59

tam ti pak vyjde argument u cosinu 9/2pí což je prakticky 1/2pí a cos 1/2 pí je nula proto reálná část je nula

lucik.kicul · 12. 06. 2010 12:01

zkusim to spočítat, děkuju =)

lucik.kicul · 12. 06. 2010 12:08

↑ Mr.Pinker:
zkusila jsem to, ale nevim jak se dostalo pí do jmenovatele, neurčuje se to pomocí kvadrantů?

Mr.Pinker · 12. 06. 2010 12:09

o to je blbost mýho zápisu pí má bejt v čitately :-D

Mr.Pinker · 12. 06. 2010 12:10

umíš napsat (-2+2i) v goniometrickým tvaru ?

lucik.kicul · 12. 06. 2010 12:12

jj, to mi problém nedělá

lucik.kicul · 12. 06. 2010 12:24

↑ Mr.Pinker:
\sprt8)*(cos\sprt2/2+isin\sprt2/2), potom mám použít moiverovu větu, že ano?

lucik.kicul · 12. 06. 2010 12:30

↑ lucik.kicul:
(\sprt8)*(cospí/4+isinpí/4)

Mr.Pinker

$(-2+2i)=\sqrt8*(\cos \frac{3\pi}{4} +i\sin\frac{3\pi}{4})$
a víš jak se používá ta věta ?

lucik.kicul · 12. 06. 2010 13:05

vím takto:(\sprt8)^6*(cos3pí/2*6+isin3pí/2*8) zbyde mi 8^3*(9pí+9pí)

lucik.kicul · 12. 06. 2010 13:09

když už jste mi poradil (děkuju =)), jak dostanu to 9pí, tak jak budu postupovat dál?

Mr.Pinker

o promin já sem myslel moc dopředu a udělal sem tam chybu:-D sou tam čtvrtiny místo polovin
a těch děvet polovin sou prakticky jedna polovina jelikož cos má periodu 2pi a jelikož cos jedné poloviny je nula
tak reálná část bude rovna nule

lucik.kicul · 12. 06. 2010 13:13

to nic =), a další postup?

Mr.Pinker · 12. 06. 2010 13:16

bude to asi tak to vypadat pak
$8^3*(0+i)=512i$
tudíš vidíš že reálná část je nulová

Matematické Fórum

#1 12. 06. 2010 08:35 — Editoval lucik.kicul (12. 06. 2010 08:49)

imaginární čísla

#2 12. 06. 2010 08:48

Re: imaginární čísla

#3 12. 06. 2010 08:49

Re: imaginární čísla

#4 12. 06. 2010 08:52

Re: imaginární čísla

#5 12. 06. 2010 08:54 — Editoval Mr.Pinker (12. 06. 2010 08:55)

Re: imaginární čísla

#6 12. 06. 2010 08:58

Re: imaginární čísla

#7 12. 06. 2010 09:02

Re: imaginární čísla

#8 12. 06. 2010 09:04

Re: imaginární čísla

#9 12. 06. 2010 11:10

Re: imaginární čísla

#10 12. 06. 2010 11:19

Re: imaginární čísla

#11 12. 06. 2010 11:51

Re: imaginární čísla

#12 12. 06. 2010 11:59

Re: imaginární čísla

#13 12. 06. 2010 12:01

Re: imaginární čísla

#14 12. 06. 2010 12:08

Re: imaginární čísla

#15 12. 06. 2010 12:09

Re: imaginární čísla

#16 12. 06. 2010 12:10

Re: imaginární čísla

#17 12. 06. 2010 12:12

Re: imaginární čísla

#18 12. 06. 2010 12:24

Re: imaginární čísla

#19 12. 06. 2010 12:30

Re: imaginární čísla

#20 12. 06. 2010 12:59 — Editoval Mr.Pinker (12. 06. 2010 13:07)

Re: imaginární čísla

#21 12. 06. 2010 13:05

Re: imaginární čísla

#22 12. 06. 2010 13:09

Re: imaginární čísla

#23 12. 06. 2010 13:10 — Editoval Mr.Pinker (12. 06. 2010 13:14)

Re: imaginární čísla

#24 12. 06. 2010 13:13

Re: imaginární čísla

#25 12. 06. 2010 13:16

Re: imaginární čísla

Zápatí