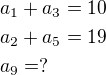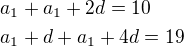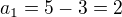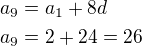Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 13. 06. 2010 14:16
- lucik.kicul
- Příspěvky: 126
- Reputace: 0
příklady
img]http://forum.matweb.cz/upload/1276431400-příklady-400.jpg[/img]
Offline
- (téma jako vyřešené označil(a) jelena)
#3 13. 06. 2010 14:19
- lucik.kicul
- Příspěvky: 126
- Reputace: 0
Re: příklady
↑ lucik.kicul:
potřebovala bych s těmito příklady poradit, hlavně s postupy. když jsem sem ten obrázek ukládala byl moc velký pak jsem ho zmenšila a je asi moc malý, že jo?
Offline
#8 13. 06. 2010 14:45 — Editoval hradecek (13. 06. 2010 14:52)
Re: příklady
1.)
Hladáš spoločné riešenie:
5.)
Netrápte sa nad svojimi problémami s matematikou, môžem vás uistiť, že tie moje sú ešte väčšie. ~~Albert Einstein~~
Jak spozná člověk, že není pitomec ? - Moudrý člověk to nepozná nikdy a blbci je to jedno. ~~Jak přicházejí básnici o iluze~~
Někteří lidi se nikdy nezmění. Anebo se rychle změní a pak se zase rychle změní nazpátek. ~~Homer Simpson~~
Offline
#14 13. 06. 2010 15:36
- lucik.kicul
- Příspěvky: 126
- Reputace: 0
Re: příklady
děkuju Vám za tyto vyřešené příklady, a nevíte ještě prosím jak vypočítat 9, a 10?
Offline
#15 13. 06. 2010 15:43 — Editoval hradecek (13. 06. 2010 15:44)
Re: příklady
Takže 8.)
Netrápte sa nad svojimi problémami s matematikou, môžem vás uistiť, že tie moje sú ešte väčšie. ~~Albert Einstein~~
Jak spozná člověk, že není pitomec ? - Moudrý člověk to nepozná nikdy a blbci je to jedno. ~~Jak přicházejí básnici o iluze~~
Někteří lidi se nikdy nezmění. Anebo se rychle změní a pak se zase rychle změní nazpátek. ~~Homer Simpson~~
Offline
#16 13. 06. 2010 15:44
Re: příklady
10)
Převeď si obě rovnice na středový tvar. Tím získáš souřadnice dvou středů, ze kterých sestav parametrickou rovnici přímky a z té pak její obecný tvar, který uprav na y=kx+q, kde k je směrnice hledané přímky.
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline



 a vypočítej rozdíl členů
a vypočítej rozdíl členů 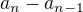
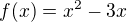 zaměň nejdřív
zaměň nejdřív  za
za  (pro f(a)) a poté za
(pro f(a)) a poté za  (pro f(a-3)). Pak sestav nerovnici.
(pro f(a-3)). Pak sestav nerovnici.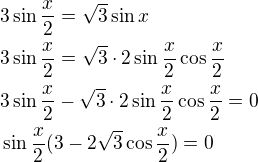

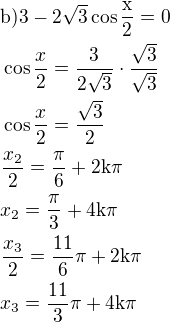
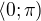 , výsledkem jsou dva kořeny.
, výsledkem jsou dva kořeny.