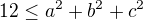Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#6 01. 08. 2010 19:50
Re: Dokaz
A co takhle?
A tedy ověřujeme, že
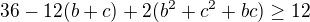

Nyní to na levé straně můžeme vyšetřit jako funkci dvou proměnných. Zkusíme najít její extrém. Začneme hledáním lokálních.![kopírovat do textarea $\partial_c[6(b+c)-(b^2+c^2+bc)]=6-2c-b$](/mathtex/f2/f27077d904195d22fc0582582fc88596.gif)
![kopírovat do textarea $\partial_b[6(b+c)-(b^2+c^2+bc)]=6-2b-c$](/mathtex/4e/4ea5066073f7098648dc69eeb30bb756.gif)
Extrém je v bodě
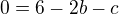
A tedy v bodě b=c=2.
Jedná se o jediný bod, kde jsou první derivace nulové a je to jediný bod podezřelý z extrému z celého R^2. Snadno se z matice druhých derivací přesvědšíem, že jde o maximum a tedy je zároveň i globálním maximem. Nejvyšší hototy výraz 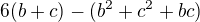 tedy nabývá pro b=c=2 a to hodnoty 12. Pak tedy
tedy nabývá pro b=c=2 a to hodnoty 12. Pak tedy
je splněno pro všechna reálná b,c.
Věřím ale, že lze nalézt nějaký více trikový postup. Já osobně vždy preferoval analýzu :-)
1 + 1 = 1 + 1
... a nebo taky ne
Offline
#7 01. 08. 2010 23:11 — Editoval pizet (02. 08. 2010 13:38)
Re: Dokaz
Ja som zas skúsil:
Vráťme sa k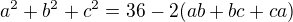
Dajme tomu, že ak 
tak určite 
A ak 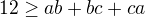 tak
tak  .
.
Z toho plynie, že táto nerovnosť 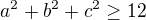 musí platiť,
musí platiť,
pretože ak dosádzame na pravej strane za  čísla z intervalu
čísla z intervalu tak sa nám zvyšuje. Tým pádom aby platila rovnosť,
tak sa nám zvyšuje. Tým pádom aby platila rovnosť,
sa musí zvyšovať aj ľavá strana t.j.  a to v inter-
a to v inter-
vale 
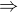
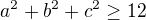 a tým pádom
a tým pádom
sme dokázali spor, čiže pôvodné tvrdenie neplatí, tak ako by aj nemalo.
P.S. Dúfam, že som tu nepopísal sprostosti ale IMHO by to malo byť správne.
PP.S. Ak som popísal hovadiny tak ma nešetrite :D.
Do you follow my way? Or you just see a black stain swimming in the Milky Way ...
KSP je určený pre študentov základných a stredných škôl, ktorí majú záujem naučiť sa niečo z oblasti algoritmov, logických úloh, programovania a informatiky.
Offline
#8 01. 08. 2010 23:31 — Editoval BrozekP (01. 08. 2010 23:33)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Dokaz
↑ pizet:
Nemůžu vyloučit, že myšlenka je správná, ale zápis je velmi špatný a nesrozumitelný. Třeba postupu
Dajme tomu, že ak
tak určite
vůbec nerozumím. To má být implikace? Pak neplatí (a=0, b=3, c=4).
To jsem vybral jednu věc z mnoha.
Offline
#9 01. 08. 2010 23:51
Re: Dokaz
↑ BrozekP: Máš pravdu.
Do you follow my way? Or you just see a black stain swimming in the Milky Way ...
KSP je určený pre študentov základných a stredných škôl, ktorí majú záujem naučiť sa niečo z oblasti algoritmov, logických úloh, programovania a informatiky.
Offline
#10 02. 08. 2010 10:16
Re: Dokaz
nechci vám tu kazit zábavu, tak jenom malý hint:
Offline
#11 02. 08. 2010 10:30
Re: Dokaz
↑ Stýv:
No pozrel som si čo to tá AG nerovnosť je a hneď mi trklo ale tu sa píše, že "... že aritmetický průměr skupiny nezáporných čísel je vždy větší nebo roven geometrickému průměru těchto čísel... ", čiže podľa toho čo tu uvádzajú by sa malo jednať o nezáporné čísla ale autor témy vravel, že majú byť reálne.
Do you follow my way? Or you just see a black stain swimming in the Milky Way ...
KSP je určený pre študentov základných a stredných škôl, ktorí majú záujem naučiť sa niečo z oblasti algoritmov, logických úloh, programovania a informatiky.
Offline
#12 02. 08. 2010 10:45
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Dokaz
↑ pizet:
Ale třeba 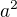 už nezáporné je.
už nezáporné je.
byk7 už sem nějaké řešení pomocí AG nerovnosti dával, nestihl jsem ho ale zkontrolovat než ho smazal, tak předpokládám, že tam měl někde drobnou chybu.
Offline
#13 02. 08. 2010 12:34
#14 02. 08. 2010 12:48
Re: Dokaz
↑ Alan122: kde jsi k té úloze vlastně přišel? přijde mi to jako typická soutěžní úloha...
Offline
#16 02. 08. 2010 13:24
Re: Dokaz
ok. kompletní řešení:
Offline
#17 02. 08. 2010 15:13 — Editoval byk7 (02. 08. 2010 15:25)
Re: Dokaz
Mám jiné řešení:
Dokážeme nerovnost (*)  ,
,
to je ale jednoduché, vyjdeme z nerovnosti mezi kvadratickým a aritmetickým průměrem.
Nerovnost vydělíme třemi a odmocníme:
Na levé straně je kvadratický průměr čísel a,b,c.
Na pravé aritmetický, platí to, protože  .
.
Tím je dokázána nerovnost (*), a z toho plyne neplatnost nerovnosti  .
.
Edit: ↑ BrozekP: chyba tam opravdu byla, a to taková, že jsem dokazoval úplně jinou neronost
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#19 02. 08. 2010 16:11 — Editoval byk7 (02. 08. 2010 16:12)
Re: Dokaz
↑ Stýv:
↑ Alan122:
kvadratický průměr se definuje jako  .
.
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
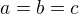

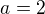
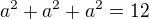


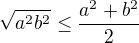
 , totéž platí pro
, totéž platí pro  a
a 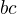 , posčítáme
, posčítáme