Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 11. 10. 2010 20:09
- princesa.keshet
- Zelenáč
- Příspěvky: 2
- Reputace: 0
konstrukční úlohy
potřebovala bych poradit se zapsáním postupu pro tyhle úlohy:
1.je dána přímka p a bod S (S neleží na přímce p). Sestrojte 6tiúhelník tak aby bod S byl jeho středem a jedna jeho strana ležela na přímce p.
2.sestrojte trojúhelník ABC pro který platí b=4cm, c=5cm, výška a= 3,5. řešte umístěním a) výškou a b) úsečkou b
3. jsou dány úsečky délek a, c, m. sestrojte rovnoramenný lichoběžník ABCD (AB je rovnoběžné s CD) tak aby úsečka AB=a, CD=c a jeho obsah se rovnal obsahu čtverce o délce strany m.
díky
Offline
#2 11. 10. 2010 20:21 — Editoval BakyX (11. 10. 2010 20:26)
Re: konstrukční úlohy
Úloha 2 - začíname výškou
1. AA0; AA0=va=3,5 cm
2. k1;k1(A;4cm)
3. p;p je kolmá na va cez A0
4. C;C leží na k1 prienik p
5. k2;k2(A;5cm)
6. B;B leží na k2 prienik p
7. Trojuholník ABC
Úloha 2 - začíname stranou "b"
1. AC;AC=b=4 cm
2. S;AS=CS; S je stred AC
3. k1;k1(S;2cm)
4. k2;k2(A;3,5 cm)
5. A0;A0 leží na k1 prienik k2
6. p;p je kolmá na AA0 cez A0
7. k3;k3(A;5cm)
8. B; B leží na k3 prienik p
9. Trojuholník ABC
1^6 - 2^6 + 3^6 = 666
Offline
#3 11. 10. 2010 20:26
- princesa.keshet
- Zelenáč
- Příspěvky: 2
- Reputace: 0
Re: konstrukční úlohy
↑ BakyX: dekuju moc :)
Offline
#4 11. 10. 2010 20:31
Re: konstrukční úlohy
Úloha 3:
Neviem, či je to dovolené, ale výšky si v pohode vypočítaš. 
Ak poznám výšku, tak to nie je problém..Ale pokiaľ by tie úsečky boli dané v rovnice a ich dĺžku by som nepoznal, tak neviem zatiaľ
1^6 - 2^6 + 3^6 = 666
Offline
#5 11. 10. 2010 20:37
Re: konstrukční úlohy
Úloha 1:
Dúfam, že ide o pravidelný šesťuholník.
1. p; S
2. r;r je kolmá na P; S 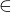 r
r
3. Q;Q leží na "r" prienik "p"
4. Uhol ASX; Uhol ASX=30 stupňov ; vytvorí polpriamku SX
5. A; A leží na "SX polpriamke" prienik p
6. JE ZVYŠOK PROBLÉM ?
1^6 - 2^6 + 3^6 = 666
Offline
#6 11. 10. 2010 22:44
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: konstrukční úlohy
↑ BakyX:
Zdravím,
ostatní konstrukce jsem neprocházela, pouze ke 3)  , odsud
, odsud  pro sestrojení výšky by se použila algebraická konstrukce - příklad (myslím, že výpočet, jako takový, není dovolen, jen odvození vztahu).
pro sestrojení výšky by se použila algebraická konstrukce - příklad (myslím, že výpočet, jako takový, není dovolen, jen odvození vztahu).
Offline
