Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Vypočtěte derivace funkcí, určete definiční obory.... (TOTO TÉMA JE VYŘEŠENÉ)
#1 02. 08. 2007 13:37
Vypočtěte derivace funkcí, určete definiční obory....
Vypočtěte derivaci funkcí, výsledek upravte. Určete definiční obory funkce i její derivace.
a) y = (ln*(1-x)) / (2)
b) y = ln odmocnina zlomku (1-sinx) / (1+sinx)
c) y = arctg (x+1) / (x-1)
Pěkně prosím - pomůžete mi s tím???
Offline
#2 03. 08. 2007 11:45
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4247
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Vypočtěte derivace funkcí, určete definiční obory....
Funkce jsou jako cibule (tím nemyslím, že smrdí). Mají vrstvy. Při derivování se právě tyto vrstvy postupně odstraňují -- vždy výsledek učíme jako
derivace_první_vrstvy*derivace_druhé_vrstvy*...*derivace_poslední_(vnitřní)_vrstvy
Funguje to tedy takto:
a) derivace logaritmu (vnější vrstvy) je 1/(1-x), derivace vnitřní vrstvy 1-x je -1. Proto
y' = -1/(1-x)/2=1/(2x-2)
b) Užitím pravidla pro logaritmy
y = 1/2*ln((1-sinx) / (1+sinx))
Derivace vnější vrstvy je (1+sinx) / (1-sinx). Vnitřní vrstva je (1-sinx) / (1+sinx)=-1+2/(1+sinx), derivace tohoto výrazu je -2/(1+sinx)^2*cos(x). (Odkud jsme to vzali? Derivace -1 je 0, k ní přičítáme opět derivaci složené funkce, jejíž vnější vrstva má derivaci 1/(1+sinx)^2, vnitřní vrstva pak cos(x)). Máme tedy vztah
y' = 1/2*(1+sinx)/(1-sinx) * (-2/(1+sinx)^2*cos(x))=
-1/((1-sinx)*(1+sinx)*cos(x))=-1/cos^3(x).
c) je analogické, nejdříve zderivujeme arctg a pak vnitřní vrstvu (ta je 1+2/(x-1), její derivace je -2/(x-1)^2).
Vyjde y'=-1/(x^2+1).
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#4 20. 08. 2007 07:13
Re: Vypočtěte derivace funkcí, určete definiční obory....
Tak jsem jela podle výpočtu Kondra a téměř na začátku jsem se hned zasekla. Nejspíš je to jen nedostatečná znalost užívání pravidel derivací, snad mi to vyjasní.
a) derivaci logaritmu chápu, pak píšeš o derivaci vnitřní vrstva 1-x, že je -1. Jak to? Proč -1?? Dejme tomu, že to tam nechám a najednou máš výsledek (1) / (2x-2) kde jsi vzal toho jmenovatele?
b) chápu derivaci odmocniny, ale nechápu, proč si najednou šoupl logaritmus, který byl před odmocninou, za odmocninu tedy za její derivaci: (1)/(2) ln Pokud to zase přeskočím, jedeme dál. Už jsem psala, že nepoznám, která vrstva je vnitřní a která vnější. Ty tady píšeš o derivaci vnější vrstvy a pak o derivaci vnitřní vrstvy, ale v obou případech derivuješ stejný výrazy. A pak celý zbytek derivací v příkladu za b) nechápu. Já zkusila zlomek zderivovat podle pravidla [(u)/(v)]´ = (u´v - uv´) / (v^2) a vyšlo mi (1)/(2) ln - cosx^2
Nejspíš blbost, tak prosím napiš, kde jsem udělala chybu a vysvětli mi ještě detailněji tvůj postup. díky
c) tady se musímhlavně zeptat na funkci arctg, jak se derivuje? Já to vůbec netuším. Pak píšeš o derivaci vnitřní vrstvy, která podle tebe je 1+2/(x-1). Nevím, kde jsi vzal 1+2 ani nevím, jestli to má být celé v čitateli nebo jednička je před zlomkem, to jsem z toho nepochopila. Pokud by to bylo v čitateli, derivovala bych přeci číslo 3 což je nula, nebo číslo 2 což je také nula, ty tam máš -2 - nevím proč. Ale pokud bych derivovala celý zlomek podle toho pravidla viz výše, vyšlo by mi to co tobě, tedy: (-2)/((x-1)^2). Jenže najednou máš psaný výsledek: -1/(x^2+1) - prosím vysvětli
děkuji
Offline
#5 20. 08. 2007 08:03
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Vypočtěte derivace funkcí, určete definiční obory....
urcite pres den se tady objevi podrobne vysvetleni, v kazdem pripade dostanes ode mne vecer mail s rucne psanou prilohou :-)
Offline
#7 20. 08. 2007 10:24
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4247
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Vypočtěte derivace funkcí, určete definiční obory....
Sandra CH napsal(a):
a) derivaci logaritmu chápu, pak píšeš o derivaci vnitřní vrstva 1-x, že je -1. Jak to? Proč -1?? Dejme tomu, že to tam nechám a najednou máš výsledek (1) / (2x-2) kde jsi vzal toho jmenovatele?
Tady jsem použil jednoduchá pravidla.
1. derivace funkce 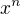 je
je  , zejména tedy derivace funkce x^1 je 1.
, zejména tedy derivace funkce x^1 je 1.
2. derivace konstanty je 0
3. (kf(x))'=kf'(x), tzn. konstantu můžeme vytknout před derivaci. Pokud je tedy derivace funkce x rovna 1, je derivace funkce -x=-1.
4. derivace součtu je součet derivací, derivace 1-x=1+(-x) je 1'+(-x)'=0+(-1)=-1.
A co se týče výsledku, tam jsem derivaci funkce ln(1-x), která je rovna 1/(x-1)*(-1)=1/(x-1) dělil dvojkou, protože funkce, kterou jsme měli zderivovat je polovinou funkce f.
Sandra CH napsal(a):
b) chápu derivaci odmocniny, ale nechápu, proč si najednou šoupl logaritmus, který byl před odmocninou, za odmocninu tedy za její derivaci: (1)/(2) ln
Jak jsem psal výše, u derivování se mi lépe pracuje s konstantami než s funkcemi. Proto jsem využil známého pravidla
ln(ab)=ln(a)+ln(b), které mj. říká, že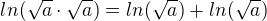 , po úpravě
, po úpravě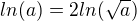 ,
,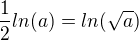
Sandra CH napsal(a):
Ty tady píšeš o derivaci vnější vrstvy a pak o derivaci vnitřní vrstvy, ale v obou případech derivuješ stejný výrazy.
Nejdřív jsem zderivoval ten logaritmus (vnější vrstvu). A protože to byl logaritmus ze zlomku
(1-sinx) / (1+sinx), dostal jsem A=(1+sinx) / (1-sinx).
Pak jsem derivoval ten zlomek (1-sinx) / (1+sinx). Osobně takovéhle věci radši převádím
na jednodušší tvar, ale možno derivovat přímo pomocí [(u)/(v)]´ = (u´v - uv´) / (v^2), což bude možná jednodušší na popis. Pro u=1-sin(x) a v=1+sin(x) je to 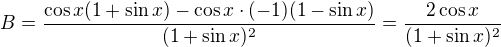 .
.
No a pak už stačí dopočítat 
Za tu třetí mocninu v první verzi výsledku se omlouvám, nějak jsem se zamotal do vlastního uzávorkování.
Sandra CH napsal(a):
c) tady se musímhlavně zeptat na funkci arctg.
Derivace funkce arctg(x) je  .
.
Sandra CH napsal(a):
Pak píšeš o derivaci vnitřní vrstvy, která podle tebe je 1+2/(x-1). Nevím, kde jsi vzal 1+2 ani nevím, jestli to má být celé v čitateli nebo jednička je před zlomkem, to jsem z toho nepochopila. Pokud by to bylo v čitateli, derivovala bych přeci číslo 3 což je nula, nebo číslo 2 což je také nula, ty tam máš -2 - nevím proč. Ale pokud bych derivovala celý zlomek podle toho pravidla viz výše, vyšlo by mi to co tobě, tedy: (-2)/((x-1)^2).
Ano, jednička měla být před zlomkem, derivace vnitřní vrstvy nám oběma vyšla (-2)/((x-1)^2).
Celkový výsledek získáme tak, že ji vynásobíme derivací vnější vrstvy, ta je po dosazeni do vzorce pro derivaci arctg rovna . Pronásobením těchto dvou výrazů dostaneme výsledek, ke kterému jsem předtím došel.
. Pronásobením těchto dvou výrazů dostaneme výsledek, ke kterému jsem předtím došel.
PS: to, co jsem takto derivoval je funkce arctg((x+1)/(x-1)),pokud byla myšlena funkce (arctg(x+1))/(x-1), je samozřejě vše úplně jinak :(
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#9 08. 03. 2008 19:04 — Editoval robert.marik (08. 03. 2008 19:05)
- robert.marik
- Einstein
- Příspěvky: 999
- Reputace: 1
Re: Vypočtěte derivace funkcí, určete definiční obory....
viz ROOM: Chtělo by to nějak zkonkretizovat, co máte na mysli. Každopádně, pokud funkce v některém bodě není definovaná, potom tam ani nemá derivaci, protože funkční hodnota v dfinici derivace figuruje.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Vypočtěte derivace funkcí, určete definiční obory.... (TOTO TÉMA JE VYŘEŠENÉ)