Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 11. 11. 2010 20:40 — Editoval Fhact0r (11. 11. 2010 20:40)
Billiard trochu jinak
Billiardový stůl má tvar pravoúhlého trojúhelníku s kratší odvěsnou délky 6 stop, jejíž protilehlý úhel má velikost 30°. (Stůl je tedy polovina rovnostranného trojúhelníku.) Z tohoto rohu je po těžnici odehrána koule (hmotný bod), která se odráží od stěn podle pravidla úhel dopadu je roven úhlu odrazu. Dokažte, že po osmi odrazech koule přijde přesně do rohu s úhlem 60°.
Nakreslil sem si to v GeoGebre, ale nejak na to nemuzu dojit. Nejakej hint? Dik moc.
math h8er
Offline
- (téma jako nevyřešené označil(a) Fhact0r)
#3 13. 11. 2010 16:09
Re: Billiard trochu jinak
Zrejme sa to dá pomocou uhlou..Musíš si doplniť každý jeden uhol a potom na základe toho, že tam máš viac pravouhlých trojuholníkov, tak nájsť nejaký pravivý vzťah. Začni so všetkými uhlami..Tá úloha je zaujímavá
1^6 - 2^6 + 3^6 = 666
Offline
#4 13. 11. 2010 17:44
Re: Billiard trochu jinak
↑ Fhact0r:Mám nápad ako na to, ale to je otročina. Pomocou analytickej geometrie 8 x opakovane vypočítavať . Včetky parametre sú presne zadané, priamky aj východzí bod.
Štart: bod B, rovnica ťažnice priesečník s AC, zistiť uhol dopadu, nastaviť uhol odrazu, vyrátať priamku odrazu, urobiť priesečník s BC, zistiť uhol dopadu, ....atď... :-) až do úspešného konca.
Offline
#5 13. 11. 2010 18:17
Re: Billiard trochu jinak
↑ pietro:
Taky me to napadlo, ale je to fakt morda. A vzhledem k tomu, ze nas profesor takove "otrocke" typy prikladu temer vubec nedava, si myslim, ze existuje i "elegantnejsi" reseni. Ale kdyz do pondeli na nic nedojdu, tak nemam na vyber.
math h8er
Offline
#6 13. 11. 2010 19:21
Re: Billiard trochu jinak
Zdravím,
Napadlo mě tohle:
Pokud S je střed strany AC, pak délka AS je 3 cm, úhel ABS je alfa, úhel ASB je beta, x je délka AB a y je délka BS, pak platí:



Snad by to šlo vyřešit a získat úhel alfa.
Všichni lidé jsou blázni, jenom já jsem letadlo.
Offline
#7 14. 11. 2010 10:49
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Billiard trochu jinak
Zdravím vás,
zkoušela jsem použit osovou souměrnost a nahradit složení osových souměrnosti jiným zobrazením, snad se mi podařilo - rotace o +60 stupňů se středem v bodě B, ale zdá se z toho dá odvodit, že to je 8 odrazů, to se mi nepovedlo.
V GeoGebře by to mělo jit tak, že k trojúhelníku přikreslím ještě jeden nahoru (přepona k přeponě), jeden dolu (dlouhá odvesná k dlouhé odvesné) (vznikne rovnostranný trojúhelník zmiňovaný v zadání) a k tomu ješt ještě jeden dolu - přepona k přeponě. Vznikne takový diamant (je v něm dobře vidět úhly, ale zda to pomůže, to nevím).
trojuhelniky se dají také naskládat za sebou (od zadaného doleva zdcadlově jeden k druhému), aby se paprsek nelámal, ale vytvořil jednu přímku, ale také nemám pocit, že by to pomohlo.
↑ Fhact0r: kterou látku berete, že je takové zadání? Děkuji.
Offline
#8 14. 11. 2010 16:35
Re: Billiard trochu jinak
↑ jelena:
Ted bereme komplexni cisla, ale to je jedno. My dostavame kazde 2 tydny 4 ulohy (na doma), ze kterych je temer vzdy pouze 1 z aktualniho uciva a dalsi 3 jsou "nahodne" (polynomicke funkce, slovni ulohy, geometrie, cokoliv co jsme nekdy brali...). A prave jedna z tech 3 je tato.
math h8er
Offline
#9 14. 11. 2010 23:14
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Billiard trochu jinak
↑ Fhact0r: děkuji, bohužel, nemám žádný jiný nápad a zřejmě to už budete zítra odevzdávat.
Snad pomůže nápověda od kolegů na "hrubou sílu", děkuji.
Offline
#10 28. 11. 2010 20:28
Re: Billiard trochu jinak
Vracim se k tomuto tematu, protoze mne o to mnozi z vas zadali. Bohuzel, stejne jako vy jsem na nic nedosel a 8-krat vypocitavat body a uhly dopadu analyzou, bylo na mne moc i vzhledem k casove tisni ve ktere sem byl. Ve skole jsme tento priklad neprobirali (a asi uz ani nebudeme), ale pokud chcete, moh by se nasho profesora zkusit zeptat jak na to.
math h8er
Offline
#11 28. 11. 2010 21:47
Re: Billiard trochu jinak
No, minimalne ja by som Ti v tom pripade bol vdacny. Ak mozes, opytaj sa. Asi treba na jednoduche vyriesenie tejto ulohy prist na nejaky trik, a triky sa oplati poznat.
Offline
#12 13. 11. 2012 00:21
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Billiard trochu jinak
Zdravím, na doporučení kolegy vanka obnovuji tuto nedořešenou úlohu.
Pokud se nezapojíte do řešení, můžete o billiardu (a nejen) i zde. Děkuji.
Offline
#13 14. 11. 2012 10:11 — Editoval Honzc (14. 11. 2012 14:54)
Re: Billiard trochu jinak
↑ jelena:
Zdravím,
tak tedy pokus o důkaz.
Pro jednoduchost položme  a pak dle zadání bude
a pak dle zadání bude 
Dále označme úhel těžnice na stranu  od strany
od strany  jako
jako 
(viz obrázek)
Nyní rozdělme stranu
 na 7 dílů, vzdálenost prvního úseku (
na 7 dílů, vzdálenost prvního úseku ( ) bude tedy
) bude tedy Spojme bod C s bodem X. (červená úsečka)
Spojme bod C s bodem X. (červená úsečka)Nyní dokážeme, že tato úsečka je shodná s posledním úsekem dráhy koule.
Vyjádříme

Podle dráhy koule jednoduše postupně vyjádříme jednotlivé úhly (v obrázku jsou jednotlivé velikosti úhlů očíslovány od 1. do 21. v pořadí odrážející se koule)
Nyní se zaměříme na poslední odraz - viz. trojúhelník

Předpokládejme nyní, že poslední odraz směřuje do bodu C.
Pak

S využitím rozdílového vzorce pro tangens a s využitím
 máme:
máme: 
a to odpovídá našemu předpokladu pro velikost úsečky

Pokud by koule nemířila do bodu C, pak by i vzdálenost

Toť vše.
Po editaci:
Poznámka: Poslední odraz koule nebude ani náhodou pod úhlem

Offline
#14 14. 11. 2012 11:10 — Editoval vanok (14. 11. 2012 11:12)
Re: Billiard trochu jinak
Pozdravujem ↑ jelena:,
Mne sa zda, ze najcitatelnejsie je riesenie vdaka osovym symetriam.( co sa mi zda dolezite, najma na urovni strednej skoly)
Navrhujem tento postup:
narysovat takuto figuru:
1° trojuholnik 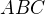
2° pridat trojuholnik  (symetricky trojuholnik trojuholnika
(symetricky trojuholnik trojuholnika 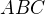 podla strany
podla strany  )
)
3°pridat trojuholnik  (symetricky trojuholnik trojuholnika
(symetricky trojuholnik trojuholnika  podla strany
podla strany  )
)
vlatne symetrie su urcene bodmy odrazu.... 8 symetrii....co nam vytvori figuru vytvorenu 9 trojuholnikmy
Obraz trasy je usecka medzi  a jeho poslednym obrazom
a jeho poslednym obrazom  .
.
Vdaka tejto figure sa velmi jednoducho dokaze otazka z cvicenia.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline

 [/img][/img]
[/img][/img]