Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Užitím logaritmické derivace vypočtěte derivace funkcí v bodě (TOTO TÉMA JE VYŘEŠENÉ)
#2 08. 08. 2007 10:01
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Užitím logaritmické derivace vypočtěte derivace funkcí v bodě
napisi pouze nastin reseni
- levou a pravou stranu zapisu f(x) zlogaritmuji prirozenym logaritmem ln
ln (f(x)) = ln((x/5)^x), trochu to upravim podle pravidel pocitani s logaritmy
ln (f(x)) = x *ln((x/5) = x*lnx - x*ln5 ted budu derivovat levou a pravou stranu zapisu
nalevo je derivace slozene funkce, napravo derivace rozdilu, ve kterem je jeste schovan "schovan" soucin
dostanu
(f´(x))/(f(x)) = (x*lnx - x*ln5)´ (pravou stranu zderivuji a upravim) a z toho vyjadrim f´(x)
f´(x) = (x*lnx - x*ln5)´ * (f(x)) na misto f(x) dam jeji zadani ln((x/5)^x)
Je mi lito, ale na podrobny vypocet ted nemam cas, snad to vylustis podle postupu, jinak az vecer :-)
Offline
#4 08. 08. 2007 14:40
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Užitím logaritmické derivace vypočtěte derivace funkcí v bodě
Možná jednodušší je popsat postup takto:
a)  . Nyní to zderivujeme jako normální složenou funkci:
. Nyní to zderivujeme jako normální složenou funkci: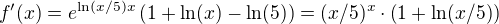
b) 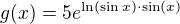 a opět normálně zderivujeme.
a opět normálně zderivujeme.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#5 08. 08. 2007 16:05
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Užitím logaritmické derivace vypočtěte derivace funkcí v bodě
Obe dve moznosti jsou dobre a zcela normalni :-)
To logaritmovani se mi zda trochu jasnejsi na vysvetleni, konec koncu ten prechod na exp. je nasledny logicky krok z logaritmovani.
Ale samozrejme muzeme popsat obe cesty (lec casu je malo :-).
Offline
#6 08. 08. 2007 17:31
Re: Užitím logaritmické derivace vypočtěte derivace funkcí v bodě
Nelze neco logaritmovat a pouzivat pravidla pro logaritmovani, pokud nevime, ze objekt, jez chceme logaritmovat nabyva na uvazovane mnozine kladne hodnoty. Tudiz spravne mi pripada reseni pomoci vztahu pro definici mocniny pomoci funkce exp(x) a log(x). Z teto definice se pak da jiste odvodit to, co zname vsichni pod pojmem pravidlo o logaritmicke derivaci.
Je to mozna pouze formalita, ale je treba to brat v uvahu. Nepochybne temito formalnimi upravami s logaritmem v tomto pripade obdrzime spravny vysledek.
Marian
Offline
#7 08. 08. 2007 19:16
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Užitím logaritmické derivace vypočtěte derivace funkcí v bodě
pro Mariana:
dekuji velmi za pripominku.
Zareagovala jsem v kontextu ostatnich prikladu od Sandry CH (zaklady mat. analyzy). Mela jsem za to, ze potrebuje vysvetlit navod na reseni podobnych prikladu (z ciste metodickeho hlediska). Proto jsem se nevenovala zdurazneni, ze tento postup (dle Sandry Ch uziti vztahu a^b = e^b*lna nebo užitím logaritmické derivace) muzeme oparvdu pouzit pouze za predpokladu, ze zaklad mocniny (at to oznacime jako a, jak oznacuje Sandra) a potazmo i cela funkce (a^b) musi byt cislo kladne. Jinak nemuzeme pouzit ani udany vztah, ani logaritmicke derivovani. Odvozovanim bychom dosli ke stejnemu vysledku.
Vzpominam si, ze postup pro pouziti pravidla logaritmicke derivace jsem cvicila se studenty dalkoveho studia VŠ a pote, co jsme to prokousali pres logaritmovani, tak to dokazali i vypocitat. Se vztahem a^b = e^b*lna meli trochu problemy, porad neco prehazovali a pletli a meli z toho i trochu strach :-) No stale plati, ze za chyby zakovy muze ucitel, nikoliv zak.
Pro Sandru CH: vztah a^b = e^b*lna nebo užití logaritmické derivace muze byt pouzito pouze v pripade, ze a > 0 ( jinak receno f(x) > 0).
Offline
#8 08. 08. 2007 23:51
Re: Užitím logaritmické derivace vypočtěte derivace funkcí v bodě
Pro jelenu:
Skoro jsem se jednou pohadal s jednim doktorandem pracujicim v oblasti globalni analyzy, ze jeho postupy nejsou korektni, pokud pouziva logaritmickou derivaci v tom smyslu, ze logaritmuje "rovnici" definujici funkcni predpis a pouziva dale pravidlo o derivaci slozene funkce. Jednou jsem na nemeckem matematickem foru www.mathscripts.de pocital podobnym zpusobem limitu a vytkli mi kolegove z Nemecka, ze nemam pravo logaritmovat neco za predpokladu, ze pracujeme s realnymi funkcemi, aniz bych overil kladnost logaritmovaneho vyrazu. Nicmene jsem je uklidnil, ze sjednam napravu a dosti zdlouhave a netrivialne jsem dokazoval pozitivnost jiste tridy funkci. Teprve pak mi to proslo.
Ja osobne volim asi radeji postup zakladajici se na definici mocniny "a na b", kde "a" je kladne. Pokud se provedou nektere vhodne didakticke kroky pri vyuce tohoto jevu (at jiz na SŠ nebo VŠ), pak si myslim, ze vypocty jsou jednoduche. Staci si vzit funkci (a ver mi, ze dela problem ji zderivovat i doktorandum) ,
,
popripade jeste komplikovanejsi funkce (maji-li smysl, nesledujici pripady jsem neoveroval), treba .
.
Postup s definici vyrazu a^b mi pripada v techto pripadech jednodussi.
Offline
#9 09. 08. 2007 07:07
Re: Užitím logaritmické derivace vypočtěte derivace funkcí v bodě
Takže Vám všem moc děkuji za příspěvky, ovšem obávám se, že pochopit derivování bez pořádného výklady pro mě není možné. Proto všechny příklady s derivací, u kterých jste mi naznačili postup, mám stále nevypočítané, protože se tím nemůžu prokousat. Pokud to ode mě není příliš velká drzost a pro Vás to není problém, prosím Vás o vyřešení všech mých příkladů s derivací a pokud možno s popsáním detailního postupu jak jste k výsledku došli, jedině tak se mi to může podařit pochopit. Moc děkuji!
Offline
#10 09. 08. 2007 20:05 — Editoval jelena (10. 08. 2007 07:44)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Užitím logaritmické derivace vypočtěte derivace funkcí v bodě
Mila Sandro CH, promin, prosim, ale musim si neco ujasnit
jelena napsal(a):
napisi pouze nastin reseni
ln (f(x)) = ln((x/5)^x)
ln (f(x)) = x *ln((x/5) = x*lnx - x*ln5
(f´(x))/(f(x)) = (x*lnx - x*ln5)´
f´(x) = (x*lnx - x*ln5)´ * (f(x))
Obecny zapis pro pouziti logaritmickeho derivovavi zni takto :
f´(x) = (ln (f (x))´ * (f(x)). postup lze pouzit za predpokladu f (x) > 0
Konkretni priklad odvozeni jsem uvedla ve sve predchozi zprave.
Resim Marianuv priklad:
f(x) = x^(x^x) predkladem je, ze x > 0
f´(x) = (ln (f (x))´ * (f(x)) = (ln ((x^(x^x))´ * (f(x)) =
((x^x)*ln ((x))´ * (f(x))
Umi doktorand derivovat soucin ((x^x)*ln ((x))´ nebo to je take problem?
- derivace vyrazu (x^x) bude podle stejne metodiky, jako to bylo popsano.
Napiste, kolegove, v cem delam chybu (jeste jednou zduraznuji, ze podminky pouziti pravidla musi byt dodrzeny)?
A vubec se nechci hadat, opravdu ne a v zadnem pripade :-) a srdecne vas zdravim
Opravila jsem chybu, spatne jsem umistila zavorky :-)
Offline
#11 09. 08. 2007 23:49 — Editoval Marian (10. 08. 2007 13:49)
Re: Užitím logaritmické derivace vypočtěte derivace funkcí v bodě
Zdravim vsechny zainteresovane!
Podrobneji osvetlim na funkci 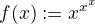 , jak ji derivovat a co vlastne symbol
, jak ji derivovat a co vlastne symbol 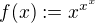 znaci. Predne tato definice:
znaci. Predne tato definice:
*****************************************************************************************
Necht  a
a 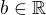 je libovolne. Pak cislo
je libovolne. Pak cislo  definujeme jako
definujeme jako
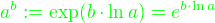 .
.
*****************************************************************************************
Tudiz napriklad podle vyse uvedene definice ,
, 
nebo ,
,  .
.
Podobne bychom mohli pokracovat dale. Nyni ale blize k vyrazu  . Oznacme
. Oznacme  . Pak podle vzse uvedene substituce s
. Pak podle vzse uvedene substituce s  a definice nahore mame
a definice nahore mame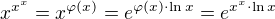 .
.
Mohli bychom jeste rozepsat vyraz 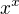 ,
,  podle definice jako
podle definice jako 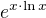 , ale zbytecne si budeme komplikovat zapis. Chtel bych na tomto miste upozornit na jednu chybu, ktere se casto dopousteji nekteri studenti. Nelze totiz psat, ze plati
, ale zbytecne si budeme komplikovat zapis. Chtel bych na tomto miste upozornit na jednu chybu, ktere se casto dopousteji nekteri studenti. Nelze totiz psat, ze plati ,
,
jak snadno nahledneme. Jinymi slovy a snad jeste trochu nazorneji: Nasledujici neplati (!!!)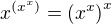 .
.
Nyni pristoupime k derivaci funkci typu  , pricemz
, pricemz  . Podle definice piseme
. Podle definice piseme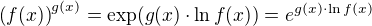 .
.
Protoze plati vztah  , lze napsat (polozime
, lze napsat (polozime 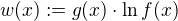 ):
): .
.
Podle pravidla o derivaci soucinu mame 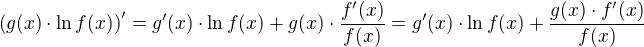 .
.
Dosazenim tohoto vztahu do predchoziho vypoctu pak snadno dostavame, ze plati .
.
Dale pouzitim definice mocniny (viz vyse) lze jednoduseji napsat 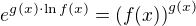 . Proto
. Proto .
.
Mozna se zda vysledek komplikovany, ale vememe si jednoduchy priklad, tedy funkci 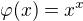 . Pak podle posledniho vzorce mame
. Pak podle posledniho vzorce mame .
.
Tento vysledek nyni pouzijeme k nalezeni derivace funkce 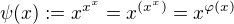 . Podle vzorce o derivaci funkce typu
. Podle vzorce o derivaci funkce typu  mame lehce, nebot polozime
mame lehce, nebot polozime  a
a 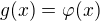 ,
, .
.
Uvedomime-li si ale, ze derivaci 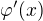 jsme jiz nasli vyse, mame za pouziti vztahu
jsme jiz nasli vyse, mame za pouziti vztahu 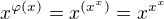 vysledek
vysledek
nebo jeste lepe .
.
Podobne bychom mohli postupovat dale a pouzit predchoziho vysledku pro nalezeni derivace funkce 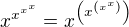 . To jiz nechavam na tech, kteri si to chteji spocitat. Pro odvazne bych tady mel jeden navrh. Definujme induktivne posloupnost funkci
. To jiz nechavam na tech, kteri si to chteji spocitat. Pro odvazne bych tady mel jeden navrh. Definujme induktivne posloupnost funkci 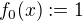 ,
, 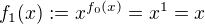 ,
, 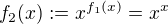 , atd. az
, atd. az 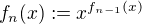 pro vsechna
pro vsechna 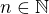 . Jak se jiste snadno ukaze, je
. Jak se jiste snadno ukaze, je ,
, 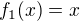 ,
,  ,
, 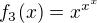 ,
, 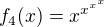 , ... .
, ... .
Derivaci funkci 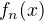 pro
pro 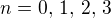 jsme jiz nasli. Uloha: "Najdete explicitni vzorec pro derivaci funkce
jsme jiz nasli. Uloha: "Najdete explicitni vzorec pro derivaci funkce 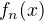 pro vsechna
pro vsechna  ."
."
Snad to stacilo a derivace podobneho typu funkci jsou jiz jasne. Chtel bych ale podotknout ze z didaktickeho hlediska je vhodne, nepouzivat vzorec, ale provest vypocet vzdy kompletne pro kazdy priklad zvlast. Naonec zjistite stejne, ze pamatovat si nejaky vzorec zabira pouze pamet. Cennejsi je vzdy si pamatovat postup jeho odvozeni. Nikdy jsem tento vzorec nepouzival ani ho nikde nevidel v knihach. Odvozoval jsem jej studentum na unverzite ve cviceni, kteri si ho cenili pro prakticky vypocet. Ale patrne jen pokud meli u sebe sesit nebo jine poznamky. Lepsi je zopakovat postup. Na druhou stranu nechci yavrhovat postup, ktery jiz zde byl popsan take, tj. zlogaritmovat vztah y=f(x)^(g(x)). Ale jak jsem jiz psal, je zapotrebi overit kladnost vyrazu na prave strane teto rovnosti. Ac se to nezda, provest to nekdy korektne je dosti slozite ve smyslu technicke narocnosti.
Budu rad, kdyz nikoho mymi zdlouhavymi poznamkami neodstrasim od derivaci realnych funkci. Naopak, potesi mne, pokud jsem tim alespon nekomu pomohl. Muze se to zdat trochu komplikovane, ale neni tomu tak. Pouzival jsem v podstate velice jednoduche a zakladni vzorce matematicke analyzy.
Zdravim.
Marian
PS: Pokud nekdo naleznete chybu, dejte vedet, prepisu to. Zatim zadnou nevidim.
Offline
#12 10. 08. 2007 07:35 — Editoval jelena (10. 08. 2007 07:38)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Užitím logaritmické derivace vypočtěte derivace funkcí v bodě
Mela jsem chybu pre prepisu a umisteni zavorek, uz je to opraveno :-)
x^(x^x) neni totez jako (x^x)^x , naprosty souhlas
x^(x^x) je tento prepis spravny, myslim, ze uz ano ?
Offline
#13 11. 08. 2007 14:14
Re: Užitím logaritmické derivace vypočtěte derivace funkcí v bodě
Zdravim jeleno!
V tom spechu jsem si nevsimnul, ze jsi vlastne polozila v tvem poslednim prispevku na toto tema dotaz. Ja myslim, ze vyraz je definovan celkem logicky tak, jak jsi to opravila a jak jsem konec koncu psal take ja, tedy pomoci zavorek takto:
je definovan celkem logicky tak, jak jsi to opravila a jak jsem konec koncu psal take ja, tedy pomoci zavorek takto: .
.
Totiz kdybychom hypoteticky definovali takto: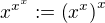 ,
,
pak bychom nedostali nic noveho ve smyslu .
.
Ze se jedna o vyraz neidenticky rovny vyrazu 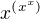 je pak zrejme z toho, ze
je pak zrejme z toho, ze 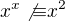 , nebot
, nebot  a
a  . Mocniny s "vice urovnemi" si pak pouzivaji pri konstrukcich velice rychle rostoucich posloupnosti realnych cisel, ktere pak maji uplatneni napriklad v teorii nekonecnych rad realnych cisel, pomoci nichz lze definovat iracionalni, transcendentni popr. Liouvillova cisla aopdobne. Ale to uz dosti odbiham. Ukazuje se tam napriklad jakou algebraickou povahu ma nekonenca rada
. Mocniny s "vice urovnemi" si pak pouzivaji pri konstrukcich velice rychle rostoucich posloupnosti realnych cisel, ktere pak maji uplatneni napriklad v teorii nekonecnych rad realnych cisel, pomoci nichz lze definovat iracionalni, transcendentni popr. Liouvillova cisla aopdobne. Ale to uz dosti odbiham. Ukazuje se tam napriklad jakou algebraickou povahu ma nekonenca rada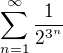
a tak.
Marian
Offline
#14 12. 08. 2007 00:28
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Užitím logaritmické derivace vypočtěte derivace funkcí v bodě
Sandra CH napsal(a):
Užitím vztahu a^b = e^b*lna nebo užitím logaritmické derivace vypočtěte derivace funkcí v bodě x = c
a) f(x) = ((x)/(5))^x; c = 5
b) g(x) = 5 * (sin x)^sinx; c = (pí)/(2)
obávám se, že pochopit derivování bez pořádného výklady pro mě není možné. Proto všechny příklady s derivací, u kterých jste mi naznačili postup, mám stále nevypočítané
Pokusim se shrnout dosavdni snahy pomoci Sandre Ch a vysledky metodicke debaty, za kterou dekuji Marianovi :-).
1. Vsechny priklady s derivaci - jak resit? - Sandro, oznac prosim, v kterem okamziku prestava byt jasno, na to se zamerim podrobne:
a) prepokladam, ze mas prostudovany nejaky uvodni teoreticky material k tematu "Derivace",
b) nekde na uvod tohoto materialu byva ukazka nebo i cviceni vypoctu derivace podle definice (o limite podilu prirustku hodnoty funkce k prirustku x) - toho se obvykle moc necvici, ale jsou zde vypocteny derivace elementarnich funkci
c) znas a umis pouzit tabulku derivaci elementarnich funkci?
d) znas pravidla pro vypocet soucinu funkce s konstantou, souctu, soucinu, podilu funkci?
e) umis poznat slozenou funkci a znas postup vypoctu derivace slozene funkce?
f) umis kombinovat pravidla c) az e) - vypocitala jsi uz nejakou derivaci samostatne az do konce (nebo vzdy to byl problem, jak pises)?
Pokud na otazky a) az f) odpovidas kladne, pristoupim k "logaritmickemu derivovani", jinak jeste jednou si, prosim, nech vysvetlit bud tady nebo od nekoho z okoli nejasny bod.
Obecne uziti vztahu a^b = e^(b*lna) nebo užití logaritmické derivace (budeme tomu tak rikat :-) se pouzije tehdy, kdyz je jednodussi derivovat ln (f(x)) nez samotnou f(x). Pozname to tak, ze f(x) se ve skutecnosti sklada se zakladu mocniny, ve kterem je e x v nejakem zapisu a exponenty (mocniny), kde je take x. Podminka f(x) vetsi 0 povinna
a) f(x) = (x/5)^x tady je to pekne videt :-) a podle tveho zadani a= (x/5), b= x
ted provedeme pouze prepis do tveho vztahu
a^b = e^(b*lna) (x/5)^x = e^(x*ln(x/5)) a budeme derivovat novy zapis funkce:
(e^(x*ln(x/5)))´ toto je funkce slozena,
vnejsi funkce e^(g (x)) , vnitrni funkce g (x) = x*ln(x/5)
vysledkem derivace slozene funkce je soucin derivace vnejsi funkce krat derivace vnitrni funkce - toto muze byt problemovy okamzik :-)
(e^(x*ln(x/5)))´ = (e^(x*ln(x/5))) * (x*ln(x/5))´
= (e^(x*ln(x/5))) * (1*ln(x/5) + x* (5/x) * 1/5) ted jen trochu upravim zavorky
= (e^(x*ln(x/5))) * (ln(x/5) + 1)
ted misto (e^(x*ln(x/5))) = (x/5)^x je to jako navrat toho zapisu, co bylo na zacatku
= ((x/5)^x) * (ln(x/5) + 1) je to stejny vysledek, jak ma kolega Kondr :-)
b) g(x) = 5 * (sin x)^sinx a podle tveho zadani a= sin x, b= sin x
5 zatim nebudu resit, jelikoz je to nasobeni s konstatntou, tak to pouze doplnim jako nasobek do zaverecneho vysledku
ted provedeme pouze prepis do tveho vztahu
a^b = e^((sin x)*ln(sin x)) (sin x)^sinx = e^((sin x)*ln(sin x)) a budeme derivovat novy zapis funkce:
(e^((sin x)*ln(sin x)))´ toto je funkce slozena,
vnejsi funkce e^(g (x)) , vnitrni funkce g (x) = (sin x)*ln(sin x)
vysledkem derivace slozene funkce je soucin derivace vnejsi funkce krat derivace vnitrni funkce
(e^((sin x)*ln(sin x)))´ = e^((sin x)*ln(sin x)) * ( (sin x)*ln(sin x))´
= e^((sin x)*ln(sin x)) (cos (x) *ln(sin x) + sin x *(1/ (sin (x)) * cos x)
= e^((sin x)*ln(sin x)) (cos (x) *ln(sin x) + cos x)
= e^((sin x)*ln(sin x)) *cos (x) *(ln(sin x) + 1) vratim puvodni zapis
((sin x)^sinx) * cos (x) *(ln(sin x) + 1)
5 * (sin x)^sinx = 5* (sin x)^sinx * cos (x) *(ln(sin x) + 1)
Pokud jsi docetla az sem, smekam :-)
Offline
#15 12. 08. 2007 00:47
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Užitím logaritmické derivace vypočtěte derivace funkcí v bodě
No a jelikoz nemam to svedomu zradit svoji vychodni variantu "logaritmickeho derivovavi" - proc by mu tak rikali, ze ? tak to zde napisi :-)
levou a pravou stranu zapisu f(x) zlogaritmuji prirozenym logaritmem ln
a)
f(x) = (x/5)^x
ln (f(x)) = ln((x/5)^x)
ln (f(x)) = x *ln((x/5) = x*lnx - x*ln5 a derivuji
(f´(x))/(f(x)) = (x*lnx - x*ln5)´
f´(x) = (x*lnx - x*ln5)´ * (f(x))
f´(x) = (1*lnx + x*1/x - ln5) * (f(x))
f´(x) = (ln (x/5 + 1) * (x/5)^x)
b)
g(x) = 5 * (sin x)^sinx
ln (g (x)) = ln (5 * (sin x)^sinx) = ln 5 + sin ln (sin (x)) derivuji
g´(x)/ g(x) = (ln 5 + sin ln (sin (x)´
g´(x) = (0 + cos (x) ln (sin (x) + sin (x) (1/sin (x)) * cos (x)) * g(x)
g´(x) = (cos (x) ln (sin (x) + cos (x)) * 5 * (sin x)^sinx
g´(x) = cos (x) * ( ln (sin (x) + 1) * 5 * (sin x)^sinx
No musite uznat, ze to lepeni e^(b*lna) a pak odlepovani je zbytecne pracne a nic neresi. podminku musime plnit i tam i tam (nebot u vaseho postupu je tez ln :-)
Offline
#16 12. 08. 2007 23:49
Re: Užitím logaritmické derivace vypočtěte derivace funkcí v bodě
Celkem jsem se pousmal nad vyrazem, ktery jsi pouzila, totiz mam na mysli to "lepeni", resp. "odlepovani". Je pravdou, ze pouziti definice mocniny s logaritmem a exponencialni funkci se muze jevit nekomu jako "lepeni". Nicmene pripada mi to elementarnejsi. Na druhou stranu z vlastni zkusenosti vim, ze studenti mivaji dosti casto dotaz, proc logaritmovat funkcni predpis y=f(x). Proc s tim neprovest neco jineho takoveho, aby to vedlo take k vysledku? Prave pak pouziti definice mocniny se muze jevit jako velice realny prostredek k vysvetleni metody logaritmickeho derivovani.
Tebou uvedeny pojem "lepeni" pak beru spise s nadsazkou, nebot vetsina dukazu je doslova lepeni. Staci si vzit treba Riemannovu vetu o prerovnani nekonecne rady. Jedna se doslova o lepeni. Podobne v algebre vety o homomorfismech a izomorfismech, potazmo o faktorovych strukturach a dalsi veci s timto souvisejici. A mohli bychom pokracovat dale.
Protoze nechci shazovat ani jednu metodu, mohu pouze nezavisle tvrdit, ze obe maji sve prednosti.
Dale nechci, at se tato diskuze odviji smerem k formalismu a tudiz bych nechal prostor ostatnim, kteri tuto diskuzi sleduji at jiz jako odbornici nebo studenti se svymi nejasnostmi pri cviceni v derivovani realnych funkci realne promenne. Kdybych mel dost casu, tak si sednu k TeXu a dam dohromady nejaky material. Bohuzel opak je pravdou. Vse, co jsem mel potrebu sdelit k temto vecem jsem patrne vycerpal.
Mym cilem bylo ukazat, ze je zapotrebi dat pozor na nekolik veci, mezi nez bezpochyby patri definice mocniny, vlastnosti logaritmu, a vyhody, resp. nevyhody obou metod derivovani. Upozornuju vsak, ze modre zaramovany vzorec dava hned vysledek. Proto bude vhodnejsi pro nekoho, koho matematika az tak nezajima a potrebuje okamzite znat vysledek a nikoliv postup. Pokud nekoho zajima postup, pak si jiste najde cas k tomu, aby dokazal nastudovat nektere veci i hloubeji, popr. reflektoval zde svoje nejasnosti. Myslim, ze toto forum prave takovemuto ucelu velmi dobre slouzi.
Marian
Offline
#17 13. 08. 2007 22:17
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Užitím logaritmické derivace vypočtěte derivace funkcí v bodě
Mariane,
srdecne zdravim a opravdu dekuji za cas, ktery byl venovan cele problematice.
Ja to vsechno chapu, uz to opravdu viz vrtat nebudu :-) .
Ted zbyva jeste zjistit, co z toho odnesla Sandra CH :-) snad se nam ozve.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Užitím logaritmické derivace vypočtěte derivace funkcí v bodě (TOTO TÉMA JE VYŘEŠENÉ)