Matematické Fórum

Když už jsme u Saturdayova vzorce, tak podle mě nespočívá v tomto konkrétním vzorečku, ale v tom, že funkci na funkci derivujeme tak, že to nejprve derivujeme jakoby byl mocněnec konstanta a pak k tomu přičteme derivaci, kterou počítáme tak, jako by byl mocnitel konstantní. Vzorec pak už z této mnemotechnické pomůcky sám vyplyne. Dal by se tedy shrnout:



Dovolil bych si ještě malé zobecnění Saturdayova vzorce, které mě napadlo díky Olinovu příspěvku (asi by se dalo lépe zformulovat):

Složitou funkci , v jejímž vyjádření pomocí jiných funkcí se x vyskytuje na n různých místech, můžeme derivovat následovně:

1. Na všech místech výskytu x ve funkci f(x) kromě prvního nahradíme x konstantou c. Poté funkci zderivujeme podle x a za c dosadíme x.
2. Na všech místech výskytu x ve funkci f(x) kromě druhého nahradíme x konstantou c. Poté funkci zderivujeme podle x a za c dosadíme x.
…
n. Na všech místech výskytu x ve funkci f(x) kromě n-tého nahradíme x konstantou c. Poté funkci zderivujeme podle x a za c dosadíme x.

Výsledky z bodů 1 až n sečteme a dostaneme tak derivaci funkce f(x) podle x.

Jednoduchým důsledkem pro 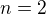a pak je klasický Saturdayův vzorec.

Důkaz zobecněného Saturdayova vzorce:

Funkci f(x) můžeme přepsat jako funkci n proměnných, kde proměnné jsou funkcemi x (přitom funkce až jsou identické funkce):



Derivujeme jako funkci více proměnných:



Toto však přesně říká dokazovaná věta.

↑ byk7:

To ne, raději bych volil název „Zobecněný Saturdayův vzorec“ :-).

↑ BrozekP:

Si si istý, že to ešte nebolo takto zovšeobecnené, že to už pomenovávate ?

↑ Stýv:

Je :-)