Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 20. 12. 2010 17:08 — Editoval Rumburak (21. 12. 2010 14:23)
Zajímavá limita
Abych také něčím přispěl:
Uvažujme  a prostor
a prostor 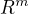 se standardní eukleidovskou metrikou
se standardní eukleidovskou metrikou  a m-rozměrnou Lebesgueovou mírou
a m-rozměrnou Lebesgueovou mírou 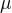 .
.
Mějme množinu  kompaktní v
kompaktní v 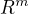 , funkci
, funkci 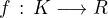 spojitou v
spojitou v  a bod
a bod  splňující
splňující
(1) 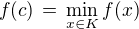 ,
,
(2)  ,
,
(3)  , kde
, kde  .
.
Určete (se zdůvodněním) limity
(*)  ,
, 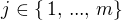 ,
,
kde 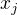 je j-tá souřadnice bodu
je j-tá souřadnice bodu  , integrály jsou m-rozměrné Lebesgueovy,
, integrály jsou m-rozměrné Lebesgueovy, 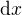 je zkratka pro
je zkratka pro  .
.
Snazší verse úlohy:
EDIT: Dodatečně si uvědomuji, že předpoklad (1) je zbytečný (vyplývá z předpokladu (2)), ale už to tak nechám.
Offline
#2 10. 02. 2015 11:17
Re: Zajímavá limita
↑ Rumburak:
Ten zlomek za limitou mi vzdáleně připomíná střední hodnotu n-rozměrného náhodného vektoru, kde 
je sdružená hustota pravděpodobnosti. Možná by bylo k řešení této úlohy použít aparát teorie pravděpodobnosti a statistiky.
Je to jen taková vágní úvaha - připomíná mi to vzdáleně mocninné průměry 
(samozřejmě v diskrétním případě), kde jeden z limitních případů (pro 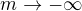 ) vede na minimum z jednotlivých členů
) vede na minimum z jednotlivých členů  , což je obdoba řešení v nápovědě.
, což je obdoba řešení v nápovědě.
Možná je vše úplně jinak a jde jen o zdání.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
 .
.