Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé středoškolské úlohy
- » Nerovnosť v trojuholníka 2 (TOTO TÉMA JE VYŘEŠENÉ)
#1 23. 12. 2010 20:11 — Editoval BakyX (23. 12. 2010 20:12)
Nerovnosť v trojuholníka 2
Zadanie: Dokáž nerovnosť platiacu pre dĺžky výšok ľubovoľného trojuholníka:
Odvodené z:
Ešte som to nevyriešil :(
Doplňujúca úloha: Zisti, kedy je výraz na ľavej strane rovný nule - bez použitia toho, čo je v HIDE
1^6 - 2^6 + 3^6 = 666
Offline
- (téma jako vyřešené označil(a) BakyX)
#2 23. 12. 2010 22:38
#3 24. 12. 2010 15:00
Offline
#4 24. 12. 2010 16:18
#5 24. 12. 2010 16:25
Re: Nerovnosť v trojuholníka 2
1^6 - 2^6 + 3^6 = 666
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé středoškolské úlohy
- » Nerovnosť v trojuholníka 2 (TOTO TÉMA JE VYŘEŠENÉ)


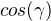 (kosinová věta)
(kosinová věta)
 . Jinak bych asi nejprve dokázal kosinovou větu :) (přes Pythagorovu nebo přes komplexní čísla).
. Jinak bych asi nejprve dokázal kosinovou větu :) (přes Pythagorovu nebo přes komplexní čísla).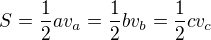 ,
,
 ,
, .
.