Matematické Fórum

Needy · 25. 01. 2011 17:25

věděl by někdo?

a) Určete dobu kmitu kapaliny o hustotě ρ, která je nalita do trubice tvaru U o průřezu S tak, že celková délka sloupce kapaliny je l.

b) Ze zákona zachování energie odvoďte pohybovou rovnici fyzického kyvadla.

zdenek1 · 25. 01. 2011 18:49

↑ Needy:

V zadání není, ale předpokládám zanedbání tření.
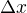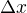Když v levém rameni stlačíš sloupec o $\Delta x$ , ve druhém rameni se vytvoří sloupec výšky $2\Delta x$ (označený tmavomodře), který vytváří hydrostatický tlak a ten tlakovou sílu $F=2\Delta x\varrho g S$ , která vrací kapalinu do rovnovážné polohy. Tato síla je proporciální výchylce $\Delta x$ , tj. je to harmonická síla. Konstanta úměrnosti je $k=2\varrho g S$ .
Pro harmonický oscilátor platí: $T=2\pi\sqrt{\frac mk}$
hmotnost kapaliny v trubici je $m=\varrho V=\varrho Sl$
Dosazením $T=2\pi\sqrt{\frac{\varrho Sl}{2\varrho g S}}=2\pi\sqrt{\frac{l}{2g}}$

Needy · 25. 01. 2011 19:34

↑ zdenek1:
dekuji

Matematické Fórum

#1 25. 01. 2011 17:25

kmity 2

#2 25. 01. 2011 18:49

Re: kmity 2

#3 25. 01. 2011 19:34

Re: kmity 2

Zápatí