Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 19. 02. 2011 13:51
Prečo táto rovnica nemá riešenie v R ?
Máme rovnicu:
Prečo nemá táto rovnica v R riešenie. Dosadím "x=2" a dostanem rovnosť. Podľa wolfrámu to má riešenie iba v C. A vlastne úprava na rovnaké základy je definované pre základy väčšie ako 0.
Mohol by mi to niekto vysvetliť ? Ďakujem
1^6 - 2^6 + 3^6 = 666
Offline
#3 19. 02. 2011 14:36
Re: Prečo táto rovnica nemá riešenie v R ?
↑ Stýv:
Mne sa to tu nezdá..
http://www.wolframalpha.com/input/?i=%2 … %28-2%29^2
1^6 - 2^6 + 3^6 = 666
Offline
#5 19. 02. 2011 14:52 — Editoval Pavel Brožek (19. 02. 2011 14:56)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Prečo táto rovnica nemá riešenie v R ?
Často se definuje pouze mocnina kladných čísel. V tomto případě, aby vůbec měla úloha smysl, musíme vzít nějakou obecnější definici. Dobrá definice mocniny komplexních čísel je tato:
Mějme komplexní čísla  a
a  . Pak
. Pak  , kde
, kde  , jestliže
, jestliže  ,
, 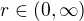 ,
, ![kopírovat do textarea $\varphi\in(-\pi,\pi]$](/mathtex/88/887dc70495fdff54d70499ea86c9796c.gif) (tomuto se říká hlavní větev logaritmu, komplexní logaritmus se dá definovat různě, ale na definici mocniny komplexního čísla to nemá vliv).
(tomuto se říká hlavní větev logaritmu, komplexní logaritmus se dá definovat různě, ale na definici mocniny komplexního čísla to nemá vliv).
S touto definicí můžeme vyjádřit levou stranu:
V našem případě je  reálné, takže můžeme psát
reálné, takže můžeme psát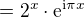
Máme tak oddělenu absolutní hodnotu čísla a komplexní jednotku. Na pravé straně je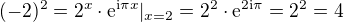 .
.
Porovnáme velikost komplexních čísel na obou stranách: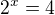
Z toho dostaneme nutně  . Snadno ověříme, že i komplexní jednotky se pro
. Snadno ověříme, že i komplexní jednotky se pro  rovnají:
rovnají:  .
.  je tedy jediným řešením v reálných číslech.
je tedy jediným řešením v reálných číslech.
Pozn.: Používám funkci  komplexní proměnné
komplexní proměnné  , tato funkce se samozřejmě musí také nějak definovat, ale to už pro naše účely snad není nutné rozebírat. Používal jsem asi jen jednu její podstatnou vlastnost:
, tato funkce se samozřejmě musí také nějak definovat, ale to už pro naše účely snad není nutné rozebírat. Používal jsem asi jen jednu její podstatnou vlastnost: 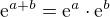 .
.
Offline