Matematické Fórum

janakolarova11 · 07. 10. 2007 17:37

prosím ještě o jeden příklad, pokud bude někdo tak hodný: Najděte matici přechodu od báze beta k bázi alfa.
alfa= ( ( 1,2,1) (2,5,2) (1,3,2))
beta= (( 4,-1,-1) (-2,1,0) (1,-1,1)) a pomocí této matice vyjádřete vektor c, který má vzhledem k bázi alfa souřadnice c=( 2,0,-3)alfa, jako lineární kombinaci vektorů z beta. Děkuji moc!

Kondr · 08. 10. 2007 22:11 — Editoval Kondr (21. 01. 2008 18:08)

EDITACE: Tento příspěvek byl přepsán tak, aby odpovídal konvencím.

Převést daný vektor do normální báze (1,0,0),(0,1,0),(0,1,1) znamená násobit ho zleva maticí báze. Pokud měl tedy v první bázi souřadnice x,y,z a ve druhé x', y', z', pak musí platit:

1 2 1 x 4 -2 1 x'
2 5 3 . y=-1 1 -1 . y'
1 2 2 z -1 0 1 z'

Symbolicky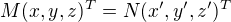
$M(x,y,z)^T=N(x',y',z')^T$
$N^{-1}M(x,y,z)^T=(x',y',z')^T$
Hledaná matice je $N^{-1}M$ .

Druhou část vyřešíš tak, že vektor c vynásobíš tou maticí $N^{-1}M$ . Kdyby byl problém s hledáním inverzní matice nebo násobením matic, ozvi se, doufám ale, že je to takto jasné.

janakolarova11 · 09. 10. 2007 16:52

strašně moc děkuji!!!!

Matematické Fórum

#1 07. 10. 2007 17:37

Matice přechodu

#2 08. 10. 2007 22:11 — Editoval Kondr (21. 01. 2008 18:08)

Re: Matice přechodu

#3 09. 10. 2007 16:52

Re: Matice přechodu

Zápatí