Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1 2
- Hlavní strana
- » Střední škola
- » Dotycnice kuzelosecky kolme na priamku (TOTO TÉMA JE VYŘEŠENÉ)
#1 21. 05. 2011 21:12 — Editoval mudrnudl (21. 05. 2011 23:53)
Dotycnice kuzelosecky kolme na priamku
Zadanie:
Napiste rovnice dotycnic danej stredovej kuzelosecky  , ktore su kolme na danu priamku
, ktore su kolme na danu priamku 
Myslim, ze pri rieseni nezalezi na tom, co je to za kuzelosecku.
Ale popravde nemam ani sajnu, co s tym urobit.
Jedine, co som zo seba vypotil je smerovy vektor priamky [1,2].
Co mam s tymto typom prikladu vobec robit? Aky je postup?
EDIT:
druhy prispevok na druhej strane tejto temy objasnuje cely postup, pre vsetkych, ktory nechcu riskovat infarkt pri citani mojich chyb
ODKAZ: http://forum.matweb.cz/viewtopic.php?pid=199995#p199995
Offline
- (téma jako vyřešené označil(a) mudrnudl)
#4 21. 05. 2011 21:22 — Editoval Phate (21. 05. 2011 21:23)
Re: Dotycnice kuzelosecky kolme na priamku
↑ mudrnudl:
Ano kruznice to je. Jak se to dela? Regularni kuzelosecky jsou v podstate tri druhu, parabola, hyperbola a elipsa, kde kruznice je specialni pripad elipsy. Na prvni pohled se to da poznat zhruba takto:
- pokud mam pouze u jedne z neznamych kvadrat a u druhe ne, je to parabola
- pokud je u obou neznamych kvadrat a u obou je kladny, tak to bude bud elipsa nebo kruznice. Pokud bude u obou neznamych stejny koeficient, tak je to kruznice, jinak je to elipsa
- pokud je u jedne z neznamych zaporny koeficient a u druhe kladny, pak je to hyperbola
Zkus tu kruznici dostat do tvaru 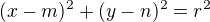 pomoci doplneni na ctverec, kde
pomoci doplneni na ctverec, kde ![kopírovat do textarea $S=[m,n]$](/mathtex/5b/5b8ba854e6eef74ca2ebfc7f5be97ab3.gif) je stred kruznice a
je stred kruznice a  je jeji polomer
je jeji polomer
Vykonávat věc, které se bojíme, je první krok k úspěchu.
Offline
#8 21. 05. 2011 21:43 — Editoval Phate (21. 05. 2011 21:44)
Re: Dotycnice kuzelosecky kolme na priamku
↑ mudrnudl:
EDIT: tusim, jsi tam chtel mit 
Ano, tedka dalsi krok, najdi obecnou rovnici primky kolme na 
Vykonávat věc, které se bojíme, je první krok k úspěchu.
Offline
#9 21. 05. 2011 21:54 — Editoval mudrnudl (21. 05. 2011 21:55)
Re: Dotycnice kuzelosecky kolme na priamku
nejsom si isty - spravil som si normalovy vektor na kolmy vektor z priamky, co je ![kopírovat do textarea $[1,2]$](/mathtex/51/51a659b04a172e54a2e9d2711817ba59.gif)
dalej som si do rovnice dosadil  a
a  , z coho mi vyslo
, z coho mi vyslo 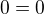 , podla mna to znamena, ze bod
, podla mna to znamena, ze bod ![kopírovat do textarea $A[-1,4]$](/mathtex/77/77155fab08677ee1b9e6ba4426aa55b0.gif) lezi na priamke,tak ho mozem pouzit pri doratavani
lezi na priamke,tak ho mozem pouzit pri doratavani  do vseobecnej rovnice:
do vseobecnej rovnice:


takze ta vseobecna by mala mat tvar:
ale samozrejme to co pisem nemusi mat ani hlavu ani patu...
Offline
#10 21. 05. 2011 21:57
Re: Dotycnice kuzelosecky kolme na priamku
↑ mudrnudl:
Prosimte, kde se vzal bod A?
Vykonávat věc, které se bojíme, je první krok k úspěchu.
Offline
#12 21. 05. 2011 22:05
Re: Dotycnice kuzelosecky kolme na priamku
↑ mudrnudl:
Nepotrebujes zjistovat zadny bod, nechas tu primku zatim obecne. Dokazes napsat primku o ktere vis jen to, ze ma normalovy vektor ![kopírovat do textarea $[1,2]$](/mathtex/51/51a659b04a172e54a2e9d2711817ba59.gif) ?
?
Vykonávat věc, které se bojíme, je první krok k úspěchu.
Offline
#14 21. 05. 2011 22:09
Re: Dotycnice kuzelosecky kolme na priamku
↑ mudrnudl:
Ano, spravne! Tedka vyuzijeme velmi mazany a vychytany figl. Jelikoz vime, ze tato primka bude tecnou nasi kruznice, tak to hlavne znamena, ze vzdalenost teto tecny od stredu kruznice bude prave polomer kruznice. Vzorecek pro vypocet vzdalenosti bodu od primky v rovine znas?
Vykonávat věc, které se bojíme, je první krok k úspěchu.
Offline
#16 21. 05. 2011 22:27 — Editoval Phate (21. 05. 2011 22:27)
Re: Dotycnice kuzelosecky kolme na priamku
↑ mudrnudl:
Ne tak docela. Vzdalenost bodu od primky vypocitame jako  , kde
, kde  a
a  jsou koeficienty u x a y v obecne rovnici a
jsou koeficienty u x a y v obecne rovnici a 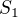 a
a  jsou souradnice bodu, od ktereho vzdalenost pocitas.
jsou souradnice bodu, od ktereho vzdalenost pocitas.  pak znaci absolutni clen v obecne rovnici, tedy ten bez nezname, bude to jedina neznama v teto rovnici, protoze u nas
pak znaci absolutni clen v obecne rovnici, tedy ten bez nezname, bude to jedina neznama v teto rovnici, protoze u nas  je to to
je to to  . Ve jmenovateli toho zlomku tedy mame velikost normaloveho vektoru, coz je odmocnina z druhych mocnin koeficientu u x a y. Tuto velikost polozime rovnu polomeru kruznice. Dulezita je ta absolutni hodnota v citateli. Zrejme totiz cekame 2 reseni ze? Protoze kdyz mame kudy primka povede, tak ji ke kruznici budeme moci "prilozit" dvemi zpusoby, je to videt? V tom bude dulezita ta absolutni hodnota, ta nam da dva ruzne vysledky pro
. Ve jmenovateli toho zlomku tedy mame velikost normaloveho vektoru, coz je odmocnina z druhych mocnin koeficientu u x a y. Tuto velikost polozime rovnu polomeru kruznice. Dulezita je ta absolutni hodnota v citateli. Zrejme totiz cekame 2 reseni ze? Protoze kdyz mame kudy primka povede, tak ji ke kruznici budeme moci "prilozit" dvemi zpusoby, je to videt? V tom bude dulezita ta absolutni hodnota, ta nam da dva ruzne vysledky pro  a tedy dve rovnobezne primky, ktere se obe budou dotykat kruznice a budou mit smerovy vektor, ktery potrebujeme. Zkus to dopocitat.
a tedy dve rovnobezne primky, ktere se obe budou dotykat kruznice a budou mit smerovy vektor, ktery potrebujeme. Zkus to dopocitat.
Vykonávat věc, které se bojíme, je první krok k úspěchu.
Offline
#18 21. 05. 2011 22:45 — Editoval Phate (21. 05. 2011 22:45)
Re: Dotycnice kuzelosecky kolme na priamku
↑ mudrnudl:
Nevyslo to dobre, mame:  , kde jsi udelal chybu?
, kde jsi udelal chybu?
Vykonávat věc, které se bojíme, je první krok k úspěchu.
Offline
#20 21. 05. 2011 22:53
Re: Dotycnice kuzelosecky kolme na priamku
↑ mudrnudl:
Je to tak, ze  , vzdy je x-ova souradnice stredu v kvadratu u x a ne u y, tam se stala chyba
, vzdy je x-ova souradnice stredu v kvadratu u x a ne u y, tam se stala chyba
Vykonávat věc, které se bojíme, je první krok k úspěchu.
Offline
#22 21. 05. 2011 23:10 — Editoval Phate (21. 05. 2011 23:11)
Re: Dotycnice kuzelosecky kolme na priamku
↑ mudrnudl:
S temi  nemuzes jen tak vylezt z absolutni hodnoty :), mas:
nemuzes jen tak vylezt z absolutni hodnoty :), mas: zkus dostat na jednu stranu abs. hodnotu a na druhou zbytek
zkus dostat na jednu stranu abs. hodnotu a na druhou zbytek
Vykonávat věc, které se bojíme, je první krok k úspěchu.
Offline
#24 21. 05. 2011 23:19 — Editoval Phate (21. 05. 2011 23:24)
Re: Dotycnice kuzelosecky kolme na priamku
↑ mudrnudl:
Ano, to je spravne, ted z toho jeste vypocist c, to uz snad zvladnes. Ohledne te absolutni hodnoty  jsem te asi zmatl.
jsem te asi zmatl.  znamena, ze je to vzdalenost, velikost, ne absolutni hodnota. Za to se omlouvam.
znamena, ze je to vzdalenost, velikost, ne absolutni hodnota. Za to se omlouvam.
EDIT: bohuzel dneska uz vypinam, tak nemuzu to dal s tebou dopocitat, doufam ze to zdarne dopocitas, kdyztak ti nekdo pomuze, kdyztak, c by ti melo vyjit:
Vykonávat věc, které se bojíme, je první krok k úspěchu.
Offline
#25 21. 05. 2011 23:22
Re: Dotycnice kuzelosecky kolme na priamku
↑ Phate:
neni sa za co ospravedlnovat, celu dobu mas so mnou trpezlivost, urcite si zasluzis 1000000000 karmy, ale mozem ti dat len 1 a neskor ked si spomenem dalsiu...
rozmyslam, ze spravim na zaver este jeden prispevok, kde dam cely postup spravne, nakolko sa v tomto nevyzna ani boh !
Offline
Stránky: 1 2
- Hlavní strana
- » Střední škola
- » Dotycnice kuzelosecky kolme na priamku (TOTO TÉMA JE VYŘEŠENÉ)


 ,
, ![kopírovat do textarea $S[1/2 , 1]$](/mathtex/9c/9c2b3b5680fcb33fd0205dd0ab44dd2c.gif)








![kopírovat do textarea $S[m,n] = [S_1,S_2] = [1,1/2]$](/mathtex/38/38a9f966228410cc0e2e6c3a00e9fe7d.gif)
 a
a  a
a 












 a
a 
 nebo
nebo