Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Určenie koeficientov polynómu II (TOTO TÉMA JE VYŘEŠENÉ)
#1 07. 06. 2011 15:10
Určenie koeficientov polynómu II
Ak sa niekomu nepozdáva VŠ sekcia, môžete to priemiestniť.
Zdravím..Ďalšia otázka..Nemám poňatia ako to zistiť:
Rozhodnite, ktorý z dvoch mnohočlenov má väčší koeficient pri mocnine x^20 a určte ich. 
Ďakujem za akúkoľvek radu.
1^6 - 2^6 + 3^6 = 666
Offline
- (téma jako vyřešené označil(a) BakyX)
#2 07. 06. 2011 15:40 — Editoval Rumburak (07. 06. 2011 15:53)
Re: Určenie koeficientov polynómu II
I. Snad někdo příjde s lepším nápadem, ale já bych to pro začátek rozepsal podle binomické věty: ,
,
z toho nás dále zajímá součet pouze těch členů, kde 2k + 3n = 20 .
Obdobně pro G(x).
EDIT:
II. Za pokus by možná i stálo zabývat se rozkladem rozdílu G(x) - F(x) podle vzorce
 .
.
Offline
#3 07. 06. 2011 17:24 — Editoval anes (07. 06. 2011 17:25)
Re: Určenie koeficientov polynómu II
Co děláš je, že se snažíš z exponentů (0,2,3) nakombinovat 20. 3 je z těch čísel jediné liché, takže v něčem, co dá x^20 musí být (-x^3) vždy "v sudé mocnině". To znamená, že (-) můžeš klidně ignorovat a pracovat s 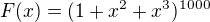
1. otázka pak už není problém :)
Offline
#4 17. 06. 2011 12:17
Re: Určenie koeficientov polynómu II
↑ anes:
Ahoj..Ďakujem za odpoveď. Zistil som, že nie je potreba určiť tie koeficienty len zistiť, ktorý je väčší. A je to problém..Môžeš sa prosím rozpísať, ako to teraz zistiť ? Ďakujem
1^6 - 2^6 + 3^6 = 666
Offline
#5 17. 06. 2011 12:23 — Editoval musixx (17. 06. 2011 12:41)
Re: Určenie koeficientov polynómu II
Jak bylo správně zdůvodněno, koeficient u  je v polynomu
je v polynomu  stejný jako v polynomu
stejný jako v polynomu  .
.
Porovnávejme tedy ten koeficient u polynomu 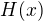 a
a 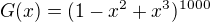 .
.
V obou dvou zníměných případech to bude součet součinů stejných kombinačních čísel, u 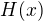 jsou všechna se znaménkem plus, zatímco u
jsou všechna se znaménkem plus, zatímco u 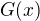 budou i nějaké mínusy. Proto je koeficient u
budou i nějaké mínusy. Proto je koeficient u  v
v 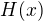 (a tedy i v
(a tedy i v  ) větší než koeficient u
) větší než koeficient u  v
v 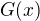 .
.
Offline
#6 17. 06. 2011 12:48
Re: Určenie koeficientov polynómu II
↑ musixx:
Ďakujem pekne. Ten program je úžašný. Keď to takto napíšeš, tak tomu rozumiem, ale v knihe je oficiálne riešenie uvedené takto:
Mnohočlen H(x)=F(-x) má u párnych mocnín "x" rovnaké koefienty ako mnohočlen F(x). Koeficient pri mocnine x^20 mnohočlenu (1+yx^2+x^3)^1000 je mnohočlen P(y) premenné "y" v tvare c1*y + c2*y^4 + c3*y^7 + c4*y^10 s kladnými koeficientmi c_i. Preto P(1)-P(-1)=2*c1 + 2*c3 > 0.
Tomuto už nerozumiem...
1^6 - 2^6 + 3^6 = 666
Offline
#7 17. 06. 2011 12:58 — Editoval musixx (17. 06. 2011 13:03)
Re: Určenie koeficientov polynómu II
c1 až c4 jsou nějaká čísla (ty výše zmíněné součty součinů kombinačních čísel, ale to není podstatné), podstatné je, že kladná, protože v polynomu (1+yx^2+x^3)^1000 proměnné x (kde y je parametr) nemá mínus "jak vzniknout".
Jak se dá x^20 poskládat z x^0, x^2 a x^3? No, x^0 tam může být kolikrát chce, ale jinak:
(x^2)^10 * (x^3)^0
(x^2)^7 * (x^3)^2
(x^2)^4 * (x^3)^4
(x^2)^1 * (x^3)^6
no a s tím x^2 se ještě pojí y na stejnou mocninu. Proto to c1*y + c2*y^4 + c3*y^7 + c4*y^10.
No a y bude jednou +1 a jednou -1. Už je jasné i to vysvětlení z tvé knížky?
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Určenie koeficientov polynómu II (TOTO TÉMA JE VYŘEŠENÉ)