Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 13. 06. 2011 07:58
Re: Cesta
↑ andynka:
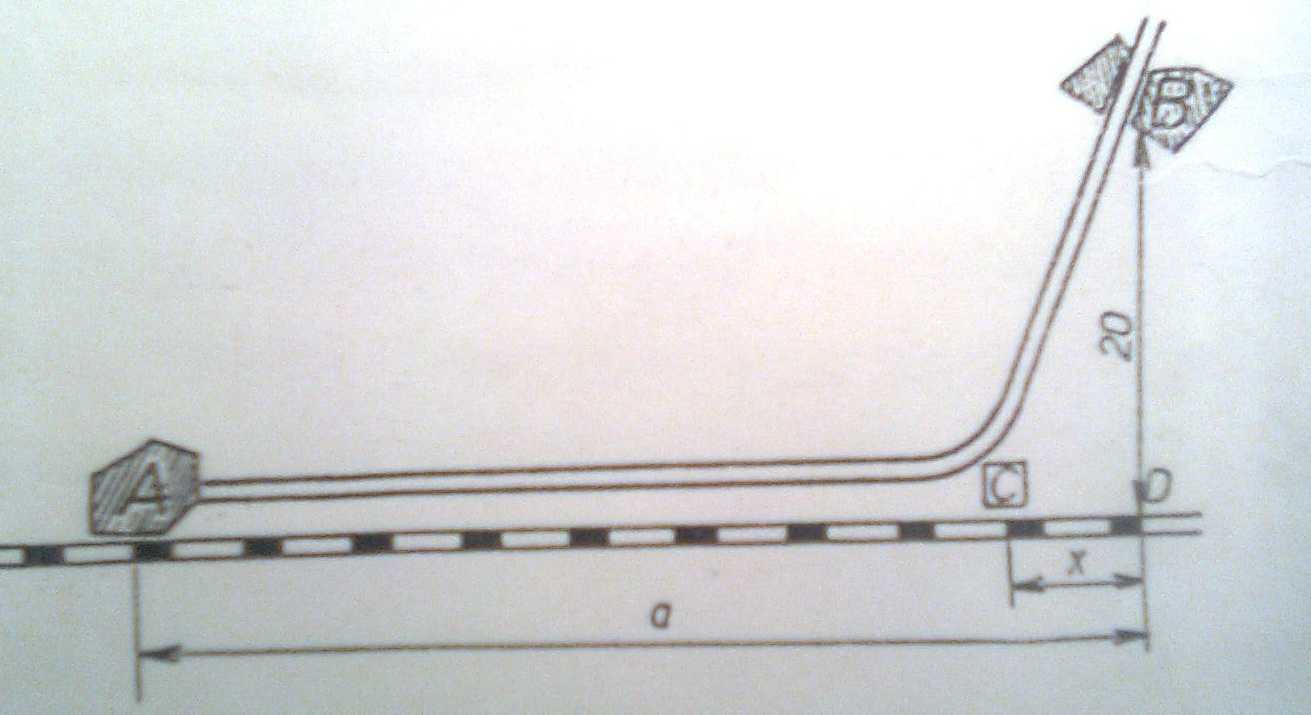
Představíme si  jako pravoúhlý trojúhelník. Jeho přepona
jako pravoúhlý trojúhelník. Jeho přepona 
Tato vzdálenost se jde pěšky dobu 
Zbytek cesty se jede vlakem 
Celá cesta trvá 
Hledáš minimum funkce  , takže si spočítáš
, takže si spočítáš
Derivovat snad umíš.
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#7 14. 06. 2011 08:06 — Editoval Cheop (15. 06. 2011 09:44)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Cesta
↑ andynka: toto derivujeme podle x a derivaci položíme = 0
toto derivujeme podle x a derivaci položíme = 0
Zastávku je třeba vybudovat přibližně 5,16 km od místa D
Nikdo není dokonalý
Offline