Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 18. 08. 2011 22:32
- check_drummer

- Příspěvky: 4631
- Reputace: 99
Re: Maximalizovanie obsahu
Vyber - a nebo dokaž, že je to on?
"Máte úhel beta." "No to nemám."
Offline
#3 18. 08. 2011 22:45
Offline
#4 19. 08. 2011 12:42 — Editoval pietro (19. 08. 2011 12:53)
Re: Maximalizovanie obsahu
↑ BakyX: Preložené do reči Pytagorasa.... Hľadáme bod na elipse, ktorý nám vytvorí so špagátom upevneným v ohniskách plošne najväčší trojuholník.
http://www.youtube.com/watch?v=HYWu7PS3 … re=related
Offline
#5 19. 08. 2011 15:26
- check_drummer

- Příspěvky: 4631
- Reputace: 99
Re: Maximalizovanie obsahu
↑ pietro:
Není to zcela ekvivalentní (resp. bylo by nutné tuto ekvivalenci dokázat) s naší úlohou. U elipsy je totiž ohnisková vzdálenost pevně dána, kdežto u hledaného trojúhelníku není dána délka ani jedné ze stran.
"Máte úhel beta." "No to nemám."
Offline
#6 26. 08. 2011 11:34 — Editoval byk7 (26. 08. 2011 11:38)
Re: Maximalizovanie obsahu
↑ check_drummer:
↑ pietro:
taky se mi to nezdá,
Nástřel řešení:
Použijeme "známého" faktu, že ze všech  -úhelníků s daným obvodem má největší obsah pravidelný
-úhelníků s daným obvodem má největší obsah pravidelný  -úhelník.
-úhelník.
Aplikací dostanem, že při daném obvodu má největší obsah rovnostranný trojúhelník.
Protože platí 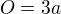 tedy
tedy 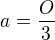 dostaneme
dostaneme 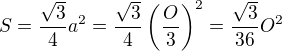
Ještě by však chtělo dokázat onen "známý" fakt.
EDIT
Možná že by to šlo přes hledaní maxima funkce 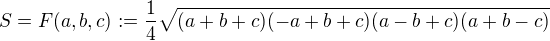 s pevným
s pevným 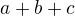 ale předpokládám, že BakyX chce spíš geometrické řešení, než analytické
ale předpokládám, že BakyX chce spíš geometrické řešení, než analytické
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#7 26. 08. 2011 12:36 — Editoval musixx (26. 08. 2011 12:50)
Re: Maximalizovanie obsahu
↑ check_drummer: Myslím si, že ekvivalentní to být může. Prostě jen přeformulujme takto: Pro jaká u a v má trojúhelník se stranami délek 1, u a v největší obsah? Obvod O pak jen dostaneme do hry scalingem (1+u+v=O), je-li to vůbec nutné. Není tak?
Offline
#8 26. 08. 2011 12:53
Re: Maximalizovanie obsahu
byk7 napsal(a):
Nástřel řešení:
Použijeme "známého" faktu, že ze všech n-úhelníků s daným obvodem má největší obsah pravidelný n-úhelník.
a za n dosadíme 3. jak prosté:D
↑ musixx: není. čím větší u a v zvolíš, tím větší dostaneš obsah. ty ale chceš dokázat, že je to u=v=1
Offline
#9 26. 08. 2011 12:58
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Maximalizovanie obsahu
↑ musixx:
To ne, to bys hledal trojúhelník, kde máš de facto pevně danou délku strany. Kdybys pak dodal podmínku "1+u+v=3", neřešil bys, jaký je největší obsah trojúhelníka daného obvodu, ale jaký je největší obsah trojúhelníka daného obvodu za předpokladu, že jedna strana je dlouhá přesně třetinu obvodu. Tedy i kdyby ti nakrásně vyšlo řešení takové úlohy "u=v=1", pak jsi ještě neuvážil všechny trojúhelníky daného obvodu, konkrétně ty, které nemají stranu délky přesně O/3.
(pozn: úloha "Pro jaká u a v (z R) má trojúhelník se stranami délek 1, u a v největší obsah?" zřejmě nemá řešení - položím-li u=v a budu zvětšovat jeho hodnotu do nekonečna, pak se i výška troj. neomezeně poroste (stačí ukázat, že 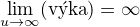 ) - neboli obsah trjúhelníka nad úsečkou(bez dalších podmínek) může být neomezeně velký)
) - neboli obsah trjúhelníka nad úsečkou(bez dalších podmínek) může být neomezeně velký)
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#10 26. 08. 2011 13:20 — Editoval musixx (26. 08. 2011 13:26)
Re: Maximalizovanie obsahu
↑ Stýv: ↑ OiBobik:. Jo, jo. Nechal jsem se unést tím příkladem elipsy a nenapsal všechno. Další podmínka je, že ta strana délky 1 je v tom trojúhelníku maximální, tedy navíc chci  . To už pak postihuje vše, souhlasíte? Výška na tu jednotkovou stranu pak je
. To už pak postihuje vše, souhlasíte? Výška na tu jednotkovou stranu pak je 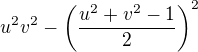 , tedy je třeba maximalizovat
, tedy je třeba maximalizovat 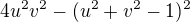 na oblasti
na oblasti  , což se snadno ukáže, že nemá lokální extrémy a vyšetřit hranici je snadné.
, což se snadno ukáže, že nemá lokální extrémy a vyšetřit hranici je snadné.
Offline
#12 26. 08. 2011 13:49 — Editoval musixx (26. 08. 2011 13:53)
Re: Maximalizovanie obsahu
↑ Stýv: ... s maximální stranou 1 ...
A kromě toho: každý trojúhelník má některou ze svých stran maximální délky. No tak si jen beru vhodné měřítko.
No a to něčemu vadí? Můj výpočet, specielně funkce 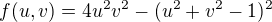 nemá na
nemá na  lokální extrém (parciální derivace
lokální extrém (parciální derivace  a
a 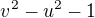 nemohou být nikdy současně nulové), je to (dle očekávání) symetrický polynom, takže vyšetření hranice stačí udělat pro u=0, kde je funkční hodnota nekladná, a pro u=1, kde je to
nemohou být nikdy současně nulové), je to (dle očekávání) symetrický polynom, takže vyšetření hranice stačí udělat pro u=0, kde je funkční hodnota nekladná, a pro u=1, kde je to 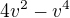 , což je maximální (a kladné) pro v=1, tedy jde o trojúhleník rovnostranný.
, což je maximální (a kladné) pro v=1, tedy jde o trojúhleník rovnostranný.
Offline
#14 26. 08. 2011 14:12 — Editoval OiBobik (26. 08. 2011 14:17)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Maximalizovanie obsahu
↑ musixx:
Já tam vidím problém v tom, že nikdy není v těch jednotlivých formulacích zahrnuta celá množina trojúhelníků se stejným obvodem (i kdyby jako podmnožina nějaké větší množiny). Z toho, jaks doplnil podmínky, plyne  , ovšem (alespoň) pro každé takové k (a zejména i pro k=2) existuje trojúhelník, který nemá žádnou stranu délky 1 a má stejný obvod (1+k), tedy jsme jej i do potenciálního důkazu nezahrnuli a nelze vyloučit, že takový trojúhelník může mít větší obsah.
, ovšem (alespoň) pro každé takové k (a zejména i pro k=2) existuje trojúhelník, který nemá žádnou stranu délky 1 a má stejný obvod (1+k), tedy jsme jej i do potenciálního důkazu nezahrnuli a nelze vyloučit, že takový trojúhelník může mít větší obsah.
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#15 26. 08. 2011 14:27
Re: Maximalizovanie obsahu
↑ Stýv: Já mám pořád pocit, že nejsem vedle. Ale raději si to ještě promyslím, ať tady teď nevařím z vody.
Byl-li by optimální poměr 8:9:10, pak by mi vyšlo buď u=0.8 a v=0.9 nebo naopak.
Možná, že přesně těmi "optimálními poměry" bych měl argumentovat. Strany každého trojúhelníka totiž ve vhodném pořadí splňují poměr u:v:1, kde  . Mám tedy pocit, že mi žádný trojúhelník neunikl. Ale v této souvislosti se ještě musím zamyslet nad argumentem ↑ OiBobik: v #14.
. Mám tedy pocit, že mi žádný trojúhelník neunikl. Ale v této souvislosti se ještě musím zamyslet nad argumentem ↑ OiBobik: v #14.
Offline
#17 26. 08. 2011 14:46
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Maximalizovanie obsahu
↑ musixx:
To je právě ono, jestli převedeš dva trojúhelníky se stejným obvodem, ale s různou délkou nejdelší strany (řekněme l,m), do tvaru u,v,1, paks je zmenšil v různých poměrech(tj 1/l a 1/m), tedy i jejich obsahy jsi zmenšil v různých poměrech (1/l^2, 1/m^2) a porovnávání obsahů těchto trojúhelníků už není validní.
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#18 26. 08. 2011 20:08 — Editoval check_drummer (27. 08. 2011 11:13)
- check_drummer

- Příspěvky: 4631
- Reputace: 99
Re: Maximalizovanie obsahu
Přiznám se, že jsem nečetl celou diskusi a musel jsem si po tom horkém dni dát jednu plzeň, ale dle mého by ta elipsa mohla pomoci:
1) Mějme nějaký trojúhelník s pevnou stranou "a" a daným obvodem, o kterém někdo tvrdí, že má maximální obsah. Pomocí té eliptické konstrukce ukážu, že musí být nutně rovnoramenný (se základnou a).
2) Mějme rovnoramenný trojúhelník se základnou "a" a daným obvodem, o kterém někdo tvrdí, že má maximální obsah.
Lze použít stejnou metodu jako v bodě 1: Vezmu jednu ze shodných stran jako vzdálenost ohnisek elipsy a pokud tento trojúhelník není rovnostranný, mohu z něj udělat trojúhelník s větším obsahem.
Tj. máme dokázáno, že pokud existuje trojúhelník s maximálním obsahem, pak je rovnostranný.
Nyní tedy zbývá ukázat, že trojúhelník s maximálním obsahem existuje. Dle mého by to šlo tak, že v prostoru délek stran a,b, které vyhovují zadání úlohy lze volit taková a,b, že a,b>=epsilon pro dostatečně malá epsilon. Jinými slovy, pokud je jedna strana hodně malá, pak se v ní maximálního obsahu nenabyde. V takovémto prostoru by pak tato a,b tvořila uzavřenou množinu, na které spojitá funkce S tedy nabývá maxima.
"Máte úhel beta." "No to nemám."
Offline
#19 26. 08. 2011 20:24
Re: Maximalizovanie obsahu
2) Mějme rovnoramenný trojúhelník se základnou "a" a daným obvodem, o kterém někdo tvrdí, že má maximální obsah.
A tady chci nějak elegantně dokázat, že musí být rovnostranný. Možná tak, že z nerovnostranného zkonstruujíi rovnostranný a co "uberu" je menší než to co "přidám". Je to dost vágní, ještě se zamyslím.
Toto jde lehce pomoci derivace, hledanim maxima, ne?
Vykonávat věc, které se bojíme, je první krok k úspěchu.
Offline
#20 26. 08. 2011 21:27
- check_drummer

- Příspěvky: 4631
- Reputace: 99
Re: Maximalizovanie obsahu
↑ Phate:
Chtěl bych něco elegantnějšího. :-)
"Máte úhel beta." "No to nemám."
Offline
#21 27. 08. 2011 11:24
Re: Maximalizovanie obsahu
Offline
#22 27. 08. 2011 12:11
- check_drummer

- Příspěvky: 4631
- Reputace: 99
Re: Maximalizovanie obsahu
↑ Honzc:
Já jsem se chtěl vyhnout derivacím. Ale když vidím ten Heronův vzorec, tak by vše šlo i jinak: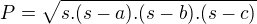 pro
pro 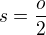 , kde o je obvod, P obsah.
, kde o je obvod, P obsah.
s je konstantní, takže maximalizujeme 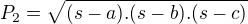 . Zkoumejme maximum
. Zkoumejme maximum ![kopírovat do textarea $P_3:=\sqrt[3]{P_2^2}$](/mathtex/92/9257e81d9e0a650054b6aae865f5d17f.gif) , zřejmě se maxima nabyde pro stejná a,b,c ať již uvažujeme
, zřejmě se maxima nabyde pro stejná a,b,c ať již uvažujeme 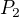 nebo
nebo 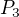 . A teď to přijde: použijeme AG nerovnost a máme
. A teď to přijde: použijeme AG nerovnost a máme 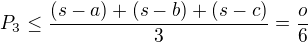 . Ovšem maxima se nabyde pro ta a,b,c, pro která je s-a=s-b=s-c, tj.
. Ovšem maxima se nabyde pro ta a,b,c, pro která je s-a=s-b=s-c, tj. , tj. a=b=c.
, tj. a=b=c.
"Máte úhel beta." "No to nemám."
Offline
#23 27. 08. 2011 13:35
Re: Maximalizovanie obsahu
↑ check_drummer: Když si pořádně přečteš můj příspěvek, tak i ↑ já: jsem vycházel z Heronova vzorce, jen jsem to upravil. :)
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#24 27. 08. 2011 14:27
- check_drummer

- Příspěvky: 4631
- Reputace: 99
Re: Maximalizovanie obsahu
↑ byk7:
Nepostupoval jsem přes derivace, takže je to snad středoškolsky dostupné vysvětlení.
Nevím, zda je požadovánoo geometrické řešení nebo jiné, já preferoval nějaké elementární.
"Máte úhel beta." "No to nemám."
Offline
#25 27. 08. 2011 18:54
Re: Maximalizovanie obsahu
↑ check_drummer: ovšem
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
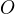 vyber ten, ktorý má najväčší obsah
vyber ten, ktorý má najväčší obsah  a urči ho.
a urči ho. 