Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#4 29. 08. 2011 14:45
Re: Těžiště 4
↑ Tomas.P: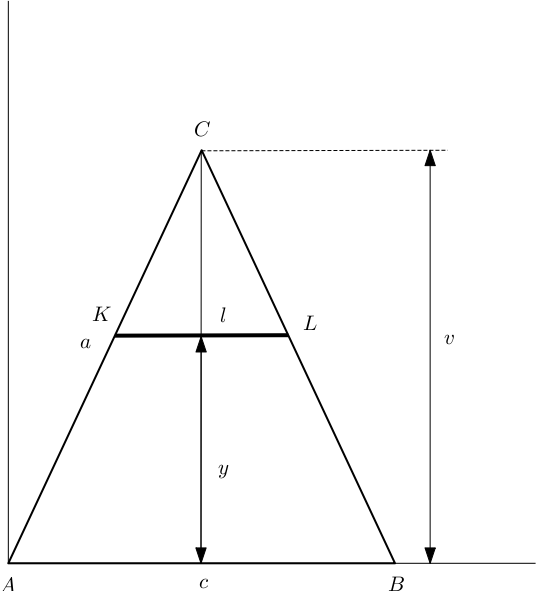
trojúhelníky 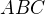 a
a  jsou podobné, takže platí (
jsou podobné, takže platí ( )
)
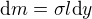

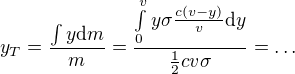
na konci pak z Pyth. vety určíš 
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
 . Výsledek
. Výsledek ![kopírovat do textarea $T=[\frac{c}{2},{\frac{1}{3}}\sqrt{{a^2}-{(\frac{c}{2})}^2}]$](/mathtex/50/509e30931103ea1feac379815c0f7dd9.gif) . Vím, že
. Vím, že