Matematické Fórum

Tomas.P

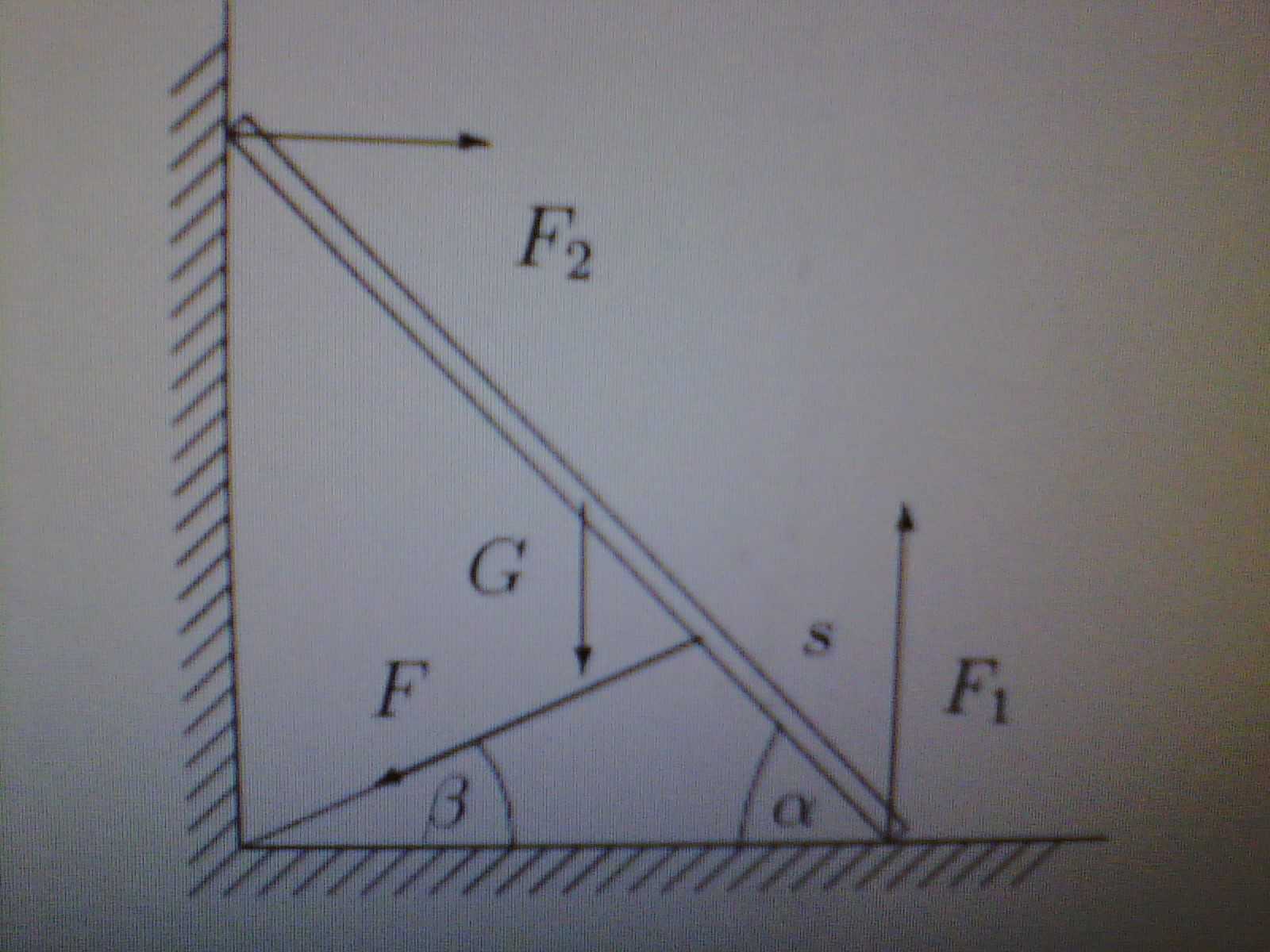
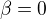Žebřík o hmotnosti $m$ stojí na hladké podlaze opřen o hladkou zeď. Aby nespadl, je v bodě $S$ přivázán provazem. Určete tahovou sílu provazu $F$ , znáte-li úhly $\alpha$ a $\beta$ . Těžiště je v polovině žebříku. Řešte nejprve obecně, pak pro speciální případ $\beta=0$ . Výsledek $F=\frac{mg}{2}cotg{\alpha}$

pepano · 14. 09. 2011 15:06

Aby byl žebřík v klidu, musí být výsledná síla a výsledný silový moment působící na žebřík nulové. Momenty budu vztahovat vzhledem k bodu S, mohli bychom zvolit i jiný libovolný pevný bod.
$F_1s \sin(90 °- \alpha) + G (\frac l2 - s) \sin(90 °- \alpha) - F_2 (l – s) \sin \alpha = 0$
Síla F se rozládá na vodorovnou složku $F'_2 = F cos \beta$
a na svislou složku $F'_1 = F sin \beta$
Pro síly $F_1 \text a F_2$ na vašem náčrtku platí $F_1 = F sin β + G$ a $F_2 = F cos \beta$ , tyto složky dosadíme do prvé rovnice:
$F_1 s \cos \alpha + G (\frac l2 - s) \cos \alpha - F_2 (l – s) \sin \alpha = 0$ ... zde jsem využil vlastnosti $\sin(90 °- \alpha) = \cos \alpha$
Nyní dosazuji:
$(F \sin \beta +G) s \cos \alpha + G (\frac l2 - s) \cos \alpha - F \cos \beta (l – s) \sin \alpha = 0$
Odtud viz http://www.wolframalpha.com/input/?i=%2 … ha%29+%3D0
$F = \frac {G l \cos \alpha}{2 (l \cos \beta \sin\alpha - s \cos\beta \sin\alpha - s \cos\alpha \sin\beta)}$
Pro $\beta = 0 \text{ je } s = 0$ a po dosazení dostaneme $F = \frac {G cos \alpha} {2 sin \alpha} = \frac {mg}{2} \text {cotg}\alpha$