Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » Vzdálenost dvou mimoběžek - pomoc s důkazem (TOTO TÉMA JE VYŘEŠENÉ)
#1 08. 09. 2011 12:37
Vzdálenost dvou mimoběžek - pomoc s důkazem
"Vzdálenost mimoběžných přímek p, q je délka úsečky PQ, kde body P, Q jsou po řadě průsečíky mimoběžek p, q s takovou příčkou mimoběžek, která je k oběma z nich kolmá."
A toto bych chtěl dokázat: "Vzdálenost mimoběžek je nejmenší ze vzdáleností bodů jedné a druhé mimoběžky."
Offline
- (téma jako vyřešené označil(a) BakyX)
#2 08. 09. 2011 12:57 — Editoval musixx (08. 09. 2011 12:59)
Re: Vzdálenost dvou mimoběžek - pomoc s důkazem
Většinou je to obáceně. Vzdálenost dvou objektů se definuje jako minimum ze vzdáleností dvou bodů, kde jeden je z jednoho objektu a druhý z druhého.
No a že v případě mimoběžek se tato minimální vzdálenost realizuje v jejich střední příčce, to je třeba dokázat.
Opravdu to chceš tak naopak, jak jsi napsal?
Offline
#4 08. 09. 2011 14:42 — Editoval Rumburak (08. 09. 2011 15:08)
Re: Vzdálenost dvou mimoběžek - pomoc s důkazem
Nechť 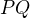 je střední příčka mimoběžek
je střední příčka mimoběžek 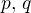 , při tom
, při tom  ,
,  .
.
Nyní uvažuj libovolné body 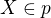 ,
, 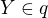 a zkoumej vzdálenost
a zkoumej vzdálenost 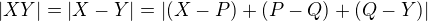 .
.
Vyjádři si její čtverec pomocí skalárního součinu a využij, že střední příčka je kolmá ke každé z daných přímek.
Cílem je ukázet, že 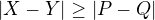 .
.
Offline
#6 09. 09. 2011 15:34 — Editoval Rumburak (09. 09. 2011 16:23)
Re: Vzdálenost dvou mimoběžek - pomoc s důkazem
↑ pepa999:
Nechť platí předpoklady a označení z ↑ Rumburak:.
Zvolme 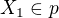 a hledejme mezi všemi body přímky
a hledejme mezi všemi body přímky  takový, který je z nich nejbliže k
takový, který je z nich nejbliže k 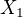 . Bude to ten bod
. Bude to ten bod 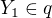 ,
,
který je patou kolmice spuštěné z bodu 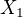 na přímku
na přímku  . O příčce
. O příčce  mimoběžek
mimoběžek  (
(
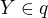 ) plyne odtud
) plyne odtud
následující:
I. Jestliže úsečka  není kolmá k přímce
není kolmá k přímce  , potom
, potom  není nejkratší příčkou mimoběžek
není nejkratší příčkou mimoběžek  .
.
II. Jestliže úsečka  není kolmá k některé z přímek
není kolmá k některé z přímek  , potom
, potom  není nejkratší příčkou mimoběžek
není nejkratší příčkou mimoběžek  .
.
Z toho je jasné, že nejkratší příčkou dvou mimoběžek může být jedině jejich střední příčka (definovaná jako jejich příčka
kolmá ke každé z nich). Co ovšem není zcela triviální, je důkaz, že střední příčka mimoběžek vůbec existuje.
Offline
#7 11. 09. 2011 00:56 — Editoval pepa999 (15. 09. 2011 23:12)
Re: Vzdálenost dvou mimoběžek - pomoc s důkazem
↑ Rumburak:
S tím důkazem mám jeden problém. Máme dokázáno, že pro každou příčku, která není kolmá alespoň k jedné z přímek p, q, existuje příčka, která je ještě kratší. Pro každou příčku, která není střední příčkou tedy platí, že není nejkratší. Zdá se mě ale, že to přímo neznamená, že střední příčka je nejkratší. Nejdřív by jsme museli dokázat, že existuje nejkratší příčka mimoběžek  .
.
Například u funkce  , pro každou její periodu existuje její další perioda, která je ještě menší, ale nejmenší periodu nemá. A nejlépe by se to dalo přirovnat k příkladu: Máme funkci
, pro každou její periodu existuje její další perioda, která je ještě menší, ale nejmenší periodu nemá. A nejlépe by se to dalo přirovnat k příkladu: Máme funkci  s definičním oborem
s definičním oborem  . Pro každou funkční hodnotu v bodech
. Pro každou funkční hodnotu v bodech 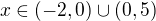 existuje
existuje 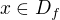 , ve kterém je funkční hodnota ještě menší. Funkční hodnota v bodě
, ve kterém je funkční hodnota ještě menší. Funkční hodnota v bodě  je tedy nejmenší.... Možná, že je toto trochu něco jiného, ale přesto mi to nepřijde úplně zřejmé.
je tedy nejmenší.... Možná, že je toto trochu něco jiného, ale přesto mi to nepřijde úplně zřejmé.
Jinak, že ke každým dvěma mimoběžkám lze vést jedinou příčku, která je k oběma z nich kolmá(střední příčku), už mám dokázané:
Při důkazu budu předpokládat větu: Odchylka dvou libovolných přímek je rovna odchylce přímek vedených libovolným bodem prostoru rovnoběžně s danými přímkami.
Uvažujme dvě mimoběžné přímky  . Uvažujme, že je sestrojena jejich příčka taková, že je k oběma z nich kolmá, označme ji
. Uvažujme, že je sestrojena jejich příčka taková, že je k oběma z nich kolmá, označme ji  . Nejdříve si vybereme nějaký libovolný bod třeba přímky
. Nejdříve si vybereme nějaký libovolný bod třeba přímky  , označme ho
, označme ho  . Tímto bodem vedeme rovnoběžku
. Tímto bodem vedeme rovnoběžku  s přímkou
s přímkou  . Přímky
. Přímky  a
a  jsou navzájem různoběžné a protínají se v bodě
jsou navzájem různoběžné a protínají se v bodě  (Kdyby byli totiž rovnoběžné, byli by i přímky
(Kdyby byli totiž rovnoběžné, byli by i přímky  a
a  navzájem rovnoběžné). Veďme bodem
navzájem rovnoběžné). Veďme bodem  přímku
přímku  , která je kolmá k přímce
, která je kolmá k přímce  i k přímce
i k přímce  (Existuje právě jedna taková přímka). Nyní uvažujme bod, ve kterém přímka
(Existuje právě jedna taková přímka). Nyní uvažujme bod, ve kterém přímka  protíná přímku
protíná přímku  , Označme ho
, Označme ho  . Je-li
. Je-li  (má být
(má být 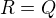 ), potom přímka
), potom přímka 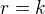 (Kdyby se totiž přímka
(Kdyby se totiž přímka  nerovnala přímce
nerovnala přímce  , nebyla by kolmá alespoň k jedné z přímek
, nebyla by kolmá alespoň k jedné z přímek  ,
,  (a tedy ani k přímce
(a tedy ani k přímce  )) a přímka
)) a přímka  tedy leží v rovině určené přímkami
tedy leží v rovině určené přímkami  a
a  . Je-li
. Je-li 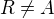 (má být
(má být  ), potom přímka
), potom přímka  je rovna rovnoběžce k přímce
je rovna rovnoběžce k přímce  , vedené bodem
, vedené bodem  (Jinak by opět nebyla kolmá k alespoň jedné z přímek
(Jinak by opět nebyla kolmá k alespoň jedné z přímek  ,
,  (a tedy ani k přímce
(a tedy ani k přímce  )) a leží tedy v rovině určené přímkami
)) a leží tedy v rovině určené přímkami  a
a  . Víme tedy, že přímka
. Víme tedy, že přímka  leží v rovině určené přímkami
leží v rovině určené přímkami  a
a  a je rovnoběžná s přímkou
a je rovnoběžná s přímkou  . Nyní uvažujme vzájemnou polohu přímky
. Nyní uvažujme vzájemnou polohu přímky  a roviny
a roviny 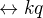 . Víme, že přímka
. Víme, že přímka  je s rovinou
je s rovinou 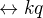 různoběžná a tedy i přímka
různoběžná a tedy i přímka  je s rovinou
je s rovinou 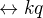 různoběžná. Přímka
různoběžná. Přímka  má tedy s rovinou
má tedy s rovinou 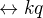 jeden společný bod, označme ho
jeden společný bod, označme ho  . Jedinou možností pro přímku
. Jedinou možností pro přímku  , která přichází v úhavu je tedy rovnoběžka vedená bodem
, která přichází v úhavu je tedy rovnoběžka vedená bodem  k přímce
k přímce  , označme ji
, označme ji  . Platí tedy: Jestliže existuje střední příčka
. Platí tedy: Jestliže existuje střední příčka  mimoběžek
mimoběžek  , potom
, potom  =
=  .Přímka
.Přímka  je skutečně střední příčkou mimoběžek
je skutečně střední příčkou mimoběžek  . Prochází přímkou
. Prochází přímkou  a je kolmá k přímkám
a je kolmá k přímkám  i
i  (je rovnoběžná s přímkou
(je rovnoběžná s přímkou  , a je tedy kolmá k přímce
, a je tedy kolmá k přímce  i
i  (a tedy i k
(a tedy i k  )). Tím je dokázáno, že ke každým dvěma mimoběžkám lze vést jedinou střední příčku, přímku
)). Tím je dokázáno, že ke každým dvěma mimoběžkám lze vést jedinou střední příčku, přímku  .
.
Offline
#8 12. 09. 2011 12:39 — Editoval Rumburak (12. 09. 2011 12:40)
Re: Vzdálenost dvou mimoběžek - pomoc s důkazem
↑ pepa999:
Z těch mých předchozích úvah opravdu plyne pouze: jediným kandidátem na nejkratší příčku (pokud taková exiatuje) je střední příčka.
Toho jsem si byl od počátku vědom a v příslušném mém příspěvku je to řečeno, i když poněkud jinými slovy.
Mylně jsem tam ovšem napsal, že není triviální dokázat existenci střední příčky (kolmé ke každé mimoběžce). Měl jsem napsat,
že není tirivální dokázat existenci nejkratší příčky, z tohoto hlediska jsem zajedno s první částí Tvého příspěvku - i příklady,
které uvádíš, jsou zcela adekvátní (v úvahách o nejmenší periodě jsi ale jistě měl na mysli funkci y = const místo y = x ) .
Tvůj důkaz existence střední příčky mi ale nepřipadá správný, protože její existenci již od začátku předpokládáš:
pepa999 napsal(a):
↑ Rumburak:
Uvažujme dvě mimoběžné přímky. Uvažujme, že je sestrojena jejich příčka taková, že je k oběma z nich kolmá, označme ji
.
Jde tedy o "důkaz kruhem" .
Postupoval bych takto:
Přímkou  proložíme rovinu
proložíme rovinu  rovnobežnou s
rovnobežnou s  - taková rovina existuje právě jedna.
- taková rovina existuje právě jedna.
Přímkou  proložíme rovinu
proložíme rovinu  kolmou k
kolmou k  - taková rovina
- taková rovina  existuje právě jedna.
existuje právě jedna.
Tyto roviny mají společnou průsečnici  , která je rovnoběžná s
, která je rovnoběžná s  , avšak různoběžná s
, avšak různoběžná s  - jejich průsečík nechť je
- jejich průsečík nechť je  .
.
Bodem  vedeme přímku
vedeme přímku  kolmou k rovině
kolmou k rovině  - taková přímka
- taková přímka  existuje právě jedna.
existuje právě jedna.
O přímce  tedy víme, že
tedy víme, že
- je kolmá k rovině  a tedy i k přímkám
a tedy i k přímkám 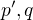 , s nimiž má společný průsečík
, s nimiž má společný průsečík  ,
,
- leží v rovině  , v níž kolmo protíná rovnoběžky
, v níž kolmo protíná rovnoběžky  . Průsečík
. Průsečík  s
s  označme
označme  .
.
Tím je dokázána existence střední příčky.
Nechť  ,
, 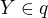 určují jinou příčku, tj. bez újmy na obecnosti
určují jinou příčku, tj. bez újmy na obecnosti  .
.
Z  spustíme kolmici na
spustíme kolmici na  , průsečík označme
, průsečík označme 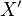 . Obrazec
. Obrazec  je obdélník, takže
je obdélník, takže 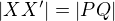 .
.
Trojúhelník  je pravoúhlý s přeponou
je pravoúhlý s přeponou  , takže
, takže  .
.
Offline
#9 12. 09. 2011 13:43
Re: Vzdálenost dvou mimoběžek - pomoc s důkazem
↑ Rumburak:
Aha, takže už tomu rozumím. Myslel jsi to tak, jak jsem na to následně zareagoval.(A v úvahách o nejmenší periodě tam mělo být opravdu y = const).
O svém důkazu si ale nemyslím, že je špatný. Za prvé, čistě logicky se mi to zdá správné. A za druhé, tato technika se dost často používá v učebnicích, ze kterých se matematiku učím(Matematika pro gymnázia - Prometheus....teď konkrétně Stereometrie). Dost často se tam vyskytuje, zejména při konstrukčních úlohách: "Předpokládejme, že je úloha vyřešena(neboli, to co chceme sestrojit, že je sestrojeno, přitom ani nevíme, jestli to sestrojit vůbec lze)". A z toho postupně vyvozujeme důsledky, a tak se začnou možnosti pro takový útvar postupně zúžovat. A až nakonec zbyde jediná možnost, tak dokážeme, že takový útvar skutenčně splňuje zadání. A pokud zadání nesplňuje, slouží tato technika jako důkaz sporem. V každém případě tímto způsobem úlohu vždycky vyřešíme, byť i třeba tak, že dokážeme, že řešení nemá. A stejným způsobem jsem postupoval i já ve svém důkazu. Můj důkaz totiž končil těmito slovy: "Jedinou možností pro přímku  , která přichází v úhavu je tedy rovnoběžka vedená bodem
, která přichází v úhavu je tedy rovnoběžka vedená bodem  k přímce
k přímce  . Tato přímka je skutečně střední příčkou mimoběžek
. Tato přímka je skutečně střední příčkou mimoběžek  . Prochází přímkou
. Prochází přímkou  a je kolmá k přímkám
a je kolmá k přímkám  i
i  (je rovnoběžná s přímkou
(je rovnoběžná s přímkou  , a je tedy kolmá k přímce
, a je tedy kolmá k přímce  i
i  (a tedy i k
(a tedy i k  ))."
))."
Offline
#10 12. 09. 2011 14:49 — Editoval Rumburak (12. 09. 2011 16:52)
Re: Vzdálenost dvou mimoběžek - pomoc s důkazem
↑ pepa999:
V Tvém důkazu vlastní problém začíná zde:
pepa999 napsal(a):
Nyní uvažujme bod, ve kterém přímka
protíná přímku
, Označme ho
. ...
Tvé úvahy před tímto bodem byly nezávislé na existenci přímky  , ale počínaje tímto bodem už nezávislé na existenci přímky
, ale počínaje tímto bodem už nezávislé na existenci přímky  nejsou.
nejsou.
Mimochodem: odkud se vzal bod  ? neměl to být spíše bod
? neměl to být spíše bod  ? Tvůj důkaz je důkazem JEDNOZNAČNOSTI přímky
? Tvůj důkaz je důkazem JEDNOZNAČNOSTI přímky  požadovaných
požadovaných
vlastností, nikoliv důkazem EXISTENCE.
Píšeš dále:
pepa999 napsal(a):
Jedinou možností pro přímku
, která přichází v úhavu je tedy rovnoběžka vedená bodem
k přímce
. Tato přímka je skutečně
střední příčkou mimoběžek. Prochází přímkou
a je kolmá k přímkám
i
(je rovnoběžná s přímkou
, a je tedy kolmá
k přímcei
(a tedy i k
)).
Přímka  opravdu má uvedené vlastnosti, ale na tom není nic divného, když to od začátku předpokládáš. Otázkou je, zda takový předpoklad
opravdu má uvedené vlastnosti, ale na tom není nic divného, když to od začátku předpokládáš. Otázkou je, zda takový předpoklad
je správný. Ze skutečnosti, že jsme nedostali spor, obecně nelze nic vyvozovat. Může to znamenat, že předpokládané tvrzení je pravdivé,
stejně dobře jako že při odvozování sporu jsme nebyli dosti šikovní. Například předpokládáme-li nesprávně, že 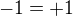 , pak umocněním
, pak umocněním
této rovnosti na druhou, což je úprava ne sice ekvivalentní, avšak přesto korektní, dostaneme 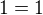 , tady pravdivou rovnost.
, tady pravdivou rovnost.
Ano, u konstruktivních úloh v první časti Rozbor se předpokládá, že je úloha vyřešena. Ale kompletní řešení má ještě další části :
Konstrukce, Důkaz, Diskuse. V části Důkaz je obecně nutno postupovat poněkud jinak, než v části Rozbor. Sice se většinou pracuje s týmiž
myšlenkami jako v Rozboru, ale v obměněném uspořádání, tak, aby to opravdu byl důkaz. Úkolem této části je korigovat případné chyby,
které by snad mohly vzniknout důsledkem příliš nespoutané fantazie v části Rozbor.
Offline
#11 12. 09. 2011 17:39 — Editoval pepa999 (15. 09. 2011 23:19)
Re: Vzdálenost dvou mimoběžek - pomoc s důkazem
↑ Rumburak:
Ano, měl to být bod  . Nejdříve jsem si ten bod označil jako
. Nejdříve jsem si ten bod označil jako  , a až potom jsem ho předělal na
, a až potom jsem ho předělal na  , podle přímky
, podle přímky  .
.
Nehledě na všechno, co tu bylo řečeno. Přímku, která mě vyšla v mém důkazu(ani tomu nemusíme říkat důkaz, ale třeba jenom postup konstrukce), si já mohu skutečně narýsovat i bez nějakých předpokladů. Klidně zde mohu napsat obměněnou verzi mého důkazu(nebo teď už opravdu spíš jenom postupu konstrukce), kde budu opravdu pouze rýsovat a nic nebudu předpokládat. A nakonec jednoduše dokážu, že narýsovaná přímka je příčka mimoběžek  ,
,  , která je k oběma z nich kolmá. Takhle by ta verze asi nějak vypadala:
, která je k oběma z nich kolmá. Takhle by ta verze asi nějak vypadala:
Uvažujme dvě mimoběžné přímky  ,
,  . Nejdříve si vybereme nějaký libovolný bod přímky
. Nejdříve si vybereme nějaký libovolný bod přímky  , označme ho
, označme ho  . Tímto bodem vedeme rovnoběžku
. Tímto bodem vedeme rovnoběžku  s přímkou
s přímkou  . Přímky
. Přímky  a
a  jsou navzájem různoběžné a protínají se v bodě
jsou navzájem různoběžné a protínají se v bodě  (Kdyby byli totiž rovnoběžné, byli by i přímky
(Kdyby byli totiž rovnoběžné, byli by i přímky  a
a  navzájem rovnoběžné). Veďme bodem
navzájem rovnoběžné). Veďme bodem  přímku
přímku  , která je kolmá k přímce
, která je kolmá k přímce  i k přímce
i k přímce  (Existuje právě jedna taková přímka).Nyní uvažujme vzájemnou polohu přímky
(Existuje právě jedna taková přímka).Nyní uvažujme vzájemnou polohu přímky  a roviny
a roviny 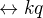 . Víme, že přímka
. Víme, že přímka  je s rovinou
je s rovinou 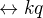 různoběžná a tedy i přímka
různoběžná a tedy i přímka  je s rovinou
je s rovinou 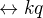 různoběžná. Přímka
různoběžná. Přímka  má tedy s rovinou
má tedy s rovinou 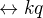 jeden společný bod, označme ho
jeden společný bod, označme ho  . Nyní sestrojme rovnoběžku vedenou bodem
. Nyní sestrojme rovnoběžku vedenou bodem  k přímce
k přímce  , označme ji
, označme ji  (má být
(má být  ). Tato přímka je střední příčkou mimoběžek
). Tato přímka je střední příčkou mimoběžek  ,
,  . Prochází totiž přímkou
. Prochází totiž přímkou  (jejím bodem
(jejím bodem  ) i
) i  (přímky
(přímky  ,
,  a bod
a bod  leží v jedné rovině. Přímka
leží v jedné rovině. Přímka  (má být
(má být  ) leží v té samé rovině. Přímka
) leží v té samé rovině. Přímka  protíná přímku
protíná přímku  a tedy i její rovnoběžku
a tedy i její rovnoběžku  ) a je kolmá k přímkám
) a je kolmá k přímkám  i
i  (je rovnoběžná s přímkou
(je rovnoběžná s přímkou  , a je tedy kolmá k přímce
, a je tedy kolmá k přímce  i
i  (a tedy i k
(a tedy i k  )).
)).
Tímto už jsem dokázal, že existuje minimálně jedna střední příčka libovolných dvou mimoběžek. To, že neexistuje, kromě přímky  (má být
(má být  ), žádná další střední příčka mimoběžek
), žádná další střední příčka mimoběžek  ,
,  jsem již dokázal ve svém prvním důkazu. Jinými slovy jsem tam dokázal: Jestliže existuje střední příčka mimoběžek
jsem již dokázal ve svém prvním důkazu. Jinými slovy jsem tam dokázal: Jestliže existuje střední příčka mimoběžek  ,
,  , je to přímka
, je to přímka  (má být
(má být  )(v mém prvním důkazu jsem ji tak neoznačoval. Neoznačoval jsem ji vlastně nijak). Nedokázal jsem hned, že to je přímka
)(v mém prvním důkazu jsem ji tak neoznačoval. Neoznačoval jsem ji vlastně nijak). Nedokázal jsem hned, že to je přímka  (má být
(má být  ), ale dokázal jsem, že jiná přímka to není. Následně jsem ale z vlastností konstrukce dokázal, že sestrojená přímaka
), ale dokázal jsem, že jiná přímka to není. Následně jsem ale z vlastností konstrukce dokázal, že sestrojená přímaka  (má být
(má být  ) je skutečně střední příčkou mimoběžek
) je skutečně střední příčkou mimoběžek  ,
,  .
.
Offline
#12 13. 09. 2011 09:36 — Editoval Rumburak (13. 09. 2011 09:40)
Re: Vzdálenost dvou mimoběžek - pomoc s důkazem
↑ pepa999:
Tento důkaz existence už je zcela správný, gratuluji ! :-)
Offline
#13 13. 09. 2011 14:43 — Editoval pepa999 (15. 09. 2011 23:20)
Re: Vzdálenost dvou mimoběžek - pomoc s důkazem
↑ Rumburak:
Tak před tím to nebylo dobře a najednou ano? Ve svém prvním důkazu jsem odvodil, co by se stalo, kdyby úplně náhodou existovala střední příčka mimoběžek  ,
,  a já ji sestrojil. Zjistil jsem, že by to byla přímka
a já ji sestrojil. Zjistil jsem, že by to byla přímka  (má být
(má být  ), kterou jsem při důkazu sestrojil(je to skutečná přímka, kterou jsem sestrojil. Ne nějaká imaginární, která může existovat pouze pokud bude splněn předpoklad. Můj předpoklad mě v sestrojování nijak neomezuje. Mohu totiž sestrojit třeba čtverec délky
), kterou jsem při důkazu sestrojil(je to skutečná přímka, kterou jsem sestrojil. Ne nějaká imaginární, která může existovat pouze pokud bude splněn předpoklad. Můj předpoklad mě v sestrojování nijak neomezuje. Mohu totiž sestrojit třeba čtverec délky 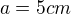 , a při tom předpokládat, že
, a při tom předpokládat, že 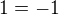 . Nikomu netvrdím, že
. Nikomu netvrdím, že 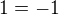 , když ten čtverec sestrojím, ale sestrojit ho mohu). Vůbec nic o té přímce nevím. Pouze vím, že Kdybych někdy v budoucnu náhodou našel nějakou střední příčku a sestrojil ji, byla by to přímka
, když ten čtverec sestrojím, ale sestrojit ho mohu). Vůbec nic o té přímce nevím. Pouze vím, že Kdybych někdy v budoucnu náhodou našel nějakou střední příčku a sestrojil ji, byla by to přímka  (má být
(má být  ). Potom úplně nezávisle na všem dokážu, že úplnou náhodou sestrojená přímka
). Potom úplně nezávisle na všem dokážu, že úplnou náhodou sestrojená přímka  (má být
(má být  ) je střední příčkou mimoběžek
) je střední příčkou mimoběžek  ,
,  . Vím tedy, že ke každým dvěma mimoběžkám lze vést alespoň jednu střední příčku(přímku
. Vím tedy, že ke každým dvěma mimoběžkám lze vést alespoň jednu střední příčku(přímku  (má být
(má být  )). Také ale vím, že když by někdo sestrojil nějakou střední příčku, byla by to přímka
)). Také ale vím, že když by někdo sestrojil nějakou střední příčku, byla by to přímka  (má být
(má být  ), takže z toho usuzuji, že žádnou další příčku sestrojit nelze. A mám tedy dokázané, že ke každým dvěma mimoběžkám lze vést právě jednu střední příčku. Kde je tady logická chyba?
), takže z toho usuzuji, že žádnou další příčku sestrojit nelze. A mám tedy dokázané, že ke každým dvěma mimoběžkám lze vést právě jednu střední příčku. Kde je tady logická chyba?
Offline
#14 13. 09. 2011 16:04 — Editoval Rumburak (13. 09. 2011 16:49)
Re: Vzdálenost dvou mimoběžek - pomoc s důkazem
↑ pepa999:
Ta POSLEDNÍ verse důkazu je správně, názor na tu první versi jsem nezměnil. V poslední versi jsi přímku  korektně našel již
korektně našel již
BEZ TOHO, ABYS JEJÍ EXISTENCI PŘEDPOKLÁDAL a právě tímto posunem jsi důkaz zkvalitnil.
"Kdyby úplně náhodou existovala střední příčka mimoběžek" ... píšeš, že tento předpoklad v původním důkaze Tě nijak neomezuje.
Nutno ovšem říci více: POMOHL TI. Kde přesně Tí pomohl, na to se sám snaž přijít - nejlépe takto:
1. Problematický důkaz si opíš bez tohoto předpokladu, ale jinak ve shodě s originálem - výstup nazvěme třeba první mutací důkazu.
2. Snaž se pochopit tu první mutaci důkazu. Pokud v ní nenajdeš žádný krok, který by se na ten vynechaný předpoklad odvolával
nebo ztratil po jeho vynechání logickou souvislost či srozumitelnost, potom nechť onen předpoklad zůstane vynechaný a všechno bude
v pořádku, první mutace se stane korektním důkazem. Ovšem pokud tam aspoň jeden takový krok bude, pak je zřejmé, že problémový
předpoklad byl použit, což je špatně s ohledem na to, co chceme dokázat. Jde o to, že logická formule 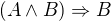 je
je
tautologií, tj. výrokem platným za všech okolností, ať již výroky A, B samy o sobě říkají cokoliv - pravdivě či nepravdivě. Dosadíme-li
za výrok B cokoliv, třebas výrok "PQ je střední příčka mimoběžek p, q" nebo naopak "mimoběžky p, q nemqjí střední příčku", samu
platnost výroku B jsme tím ještě nedokázali.
Postupným nahrazováním problémových kroků první mutace kroky jinými - již nezávislými na vynechaném předpokldau - můžeme vytvářet
mutace další a tím důkaz ladit.
Neříkám, že ve Tvém původním důkaze je bezcenné úplně všechno, ale matematický důkaz je poměrně formální záležitostí, toho nutno
dbát a z tohoto hlediska jsem ho posuzoval. Snad se mi podařilo tu formální chybu objasnit. Aby někdo druhý mohl formálně chybný
důkaz akceptovat po věcné stránce, musel by si ho napřed odladit výše popsaným způsobem, což je i poměrně pracné a čtenáři to ani
nepřísluší - taková práce přísluší pouze a jedině autorovi důkazu.
Offline
#15 15. 09. 2011 11:57 Příspěvek uživatele pepa999 byl skryt uživatelem pepa999.
#16 15. 09. 2011 12:31 — Editoval pepa999 (15. 09. 2011 23:26)
Re: Vzdálenost dvou mimoběžek - pomoc s důkazem
↑ Rumburak:
Abych pravdu řekl, ještě mi pořád není jasné, kde přesně se moje chyba nachází a kde přesně mi ten předpoklad pomohl. A za tu první mutaci mého důkazu považuji "druhou verzi" mého důkazu. A kdybych ji před tím nenapsal, teď bych ji napsal úplně stejně, protože jak jsem říkal, ty předpoklady mě v ničem neomezují, takže bych prostě jenom napsal tu konstrukci bez ničeho dalšího. A kde že mi ten předpoklad pomohl? Popravdě ještě úplně nevím, co přesně označuješ za chybné, a jelikož ještě stále považuji svůj první důkaz za správný, řeknu, že mi pomohl v tom, abych věděl, jak má vypadat moje knstrukce. A nevím, kde přesně je podle Tebe chyba, neboli, kde přesně se nachází ona tautologie.
Možná, že je zde jeden problém. Označuješ matematický důkazu za "poměrně formální" věc. A já vlastně ani žádnou definici matematického důkazu neznám. Podíval jsem se na wikipedii, kde je matematický důkaz označem jako "demonstrace nutné pravdivosti nějakého tvrzení za určitých předpokladů (axiomů)". S touto definicí ale nebude o moc jednodušší najít onu tautologii. Mám ale pocit, že akceptuješ pouze jednu formu důkazu, a jinou ne, i když je to třeba také demonstrace nutné pravdivosti, i když jiným způsobem. A nebo, že můj důkaz chápeš jinak, než je myšlený a vidíš tautologii tam, kde ve skutečnosti není. A nebo, že se tam tautologie opravdu někde nachází. I když, nedokážu si představit, že by jsem opravdu přišel na to, že je ten důkaz špatně, protože já si touto formou dokazuji v matematice většinu věcí. Občas používám i tu druhou formu. Ale ta první se mě zdá efektivnější, objevím hned množinu všech řešení.(Předpokládám, že je důkaz správně). Při té druhé formě najdu maximálně řešení jedno a potom ještě musím zvlášť dokazovat, že další neexistují. A k tomu ladění důkazu. S tím naplno souhlasím, že to by měl dělat pouze autor. Ale já si myslím, že už ta první verze mého důkazu je správná a o tom tě chci přesvědčit.
Pokusím se ti teď popsat, proč si ještě pořád myslím, že je můj důkaz správně: Žádný člověk na světě mě nemůže sestrojit jinou střední příčku mimoběžek  ,
,  , než je přímka
, než je přímka  (má být
(má být  ), protože můj první důkaz je vlastně postup, který tento člověk bude splňovat, pokud by sestrojil nějakou střední příčku dvou nějakých mimoběžek
), protože můj první důkaz je vlastně postup, který tento člověk bude splňovat, pokud by sestrojil nějakou střední příčku dvou nějakých mimoběžek  ,
,  . Takový člověk bude splňovat každý krok mého důkazu a logicky si odvodím, že sestrojil přímku
. Takový člověk bude splňovat každý krok mého důkazu a logicky si odvodím, že sestrojil přímku  (má být
(má být  ). A ten důkaz opravdu závisí na existenci té střední příčky, to nepopírám. Je to totiž úvaha pro případ, že střední příčka existuje a někdo ji sestrojí. Co je na tom špatného? Na konci důkazu tedy vím, že buď střední příčka neexistuje, nebo je to přímka
). A ten důkaz opravdu závisí na existenci té střední příčky, to nepopírám. Je to totiž úvaha pro případ, že střední příčka existuje a někdo ji sestrojí. Co je na tom špatného? Na konci důkazu tedy vím, že buď střední příčka neexistuje, nebo je to přímka  (má být
(má být  ). Kde je zde tautologie? Na konci důkazu jsem si ještě dokázal z vlastností konstrukce, že příčka
). Kde je zde tautologie? Na konci důkazu jsem si ještě dokázal z vlastností konstrukce, že příčka  (má být
(má být  ) je střední příčkou******.A díky tomu, že jsem si vyřešil tento případ, že střední příčka existuje, vím, že už žádná další neexistuje. První verze mého důkazu je pro mě demonstrace nutné pravdivosti.
) je střední příčkou******.A díky tomu, že jsem si vyřešil tento případ, že střední příčka existuje, vím, že už žádná další neexistuje. První verze mého důkazu je pro mě demonstrace nutné pravdivosti.
Napadla mě ještě třetí verze mého důkazu, která bude stejně efektivní, jako ta první, ale nebude nic předpokládat. A v podstatě bych první a třetí verzi označil za shodné, i když řečené trochu jiným způsobem.
Uvažujme dvě mimoběžné přímky  ,
,  . Nejdříve si vybereme nějaký libovolný bod přímky
. Nejdříve si vybereme nějaký libovolný bod přímky  , označme ho
, označme ho  . Tímto bodem vedeme rovnoběžku
. Tímto bodem vedeme rovnoběžku  s přímkou
s přímkou  . Přímky
. Přímky  a
a  jsou navzájem různoběžné a protínají se v bodě
jsou navzájem různoběžné a protínají se v bodě  (Kdyby byli totiž rovnoběžné, byli by i přímky
(Kdyby byli totiž rovnoběžné, byli by i přímky  a
a  navzájem rovnoběžné). Veďme bodem
navzájem rovnoběžné). Veďme bodem  přímku
přímku  , která je kolmá k přímce
, která je kolmá k přímce  i k přímce
i k přímce  (Existuje právě jedna taková přímka). Nyní uvažujme libovolnou příčku mimoběžek
(Existuje právě jedna taková přímka). Nyní uvažujme libovolnou příčku mimoběžek  ,
,  , která neleží v rovině
, která neleží v rovině 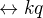 . Taková příčka není rovnoběžná s přímkou
. Taková příčka není rovnoběžná s přímkou  (A není tedy kolmá k alespoň jedné z přímek
(A není tedy kolmá k alespoň jedné z přímek  ,
,  (a tedy ani k přímce
(a tedy ani k přímce  )) a není tedy střední příčkou mimoběžek
)) a není tedy střední příčkou mimoběžek  ,
,  . V úvahu pro střední příčku tedy připadají pouze příčky, které leží v rovině
. V úvahu pro střední příčku tedy připadají pouze příčky, které leží v rovině 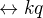 . Nyní uvažujme vzájemnou polohu přímky
. Nyní uvažujme vzájemnou polohu přímky  a roviny
a roviny 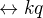 . Víme, že přímka
. Víme, že přímka  je s rovinou
je s rovinou 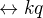 různoběžná a tedy i přímka
různoběžná a tedy i přímka  je s rovinou
je s rovinou 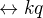 různoběžná. Přímka
různoběžná. Přímka  má tedy s rovinou
má tedy s rovinou 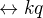 jeden společný bod, označme ho
jeden společný bod, označme ho  . Nyní uvažujme všechny příčky mimoběžek
. Nyní uvažujme všechny příčky mimoběžek  ,
,  , které leží v rovině
, které leží v rovině 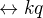 . Pro všechny takové příčky platí, že prochází bodem
. Pro všechny takové příčky platí, že prochází bodem  . Nyní uvažujme ty z nich, které nejsou rovnoběžné s přímkou
. Nyní uvažujme ty z nich, které nejsou rovnoběžné s přímkou  . Ty nejsou kolmé k alespoň jedné z přímek
. Ty nejsou kolmé k alespoň jedné z přímek  ,
,  (a tedy ani k přímce
(a tedy ani k přímce  ) a žádná z nich tedy není střední příčkou mimoběžek
) a žádná z nich tedy není střední příčkou mimoběžek  ,
,  . V úvahu pro střední příčku tedy připadá již pouze jediná příčka. Rovnoběžka s přímkou
. V úvahu pro střední příčku tedy připadá již pouze jediná příčka. Rovnoběžka s přímkou  , procházející bodem
, procházející bodem  . Označme ji
. Označme ji  . Tato přímka je střední příčkou mimoběžek
. Tato přímka je střední příčkou mimoběžek  ,
,  . Prochází totiž přímkou
. Prochází totiž přímkou  (jejím bodem
(jejím bodem  ) i
) i  (přímky
(přímky  ,
,  a bod
a bod  leží v jedné rovině. Přímka
leží v jedné rovině. Přímka  leží v té samé rovině. Přímka
leží v té samé rovině. Přímka  protíná přímku
protíná přímku  a tedy i její rovnoběžku
a tedy i její rovnoběžku  ) a je kolmá k přímkám
) a je kolmá k přímkám  i
i  (je rovnoběžná s přímkou
(je rovnoběžná s přímkou  , a je tedy kolmá k přímce
, a je tedy kolmá k přímce  i
i  (a tedy i k
(a tedy i k  )). Tím je dokázáno, že ke každým dvěma mimoběžkám lze vést jedinou střední příčku.
)). Tím je dokázáno, že ke každým dvěma mimoběžkám lze vést jedinou střední příčku.
****** Možná, že právě tady je ten kámen úrazu. Podle tvého názoru na tom není nic divného, že přímka  (má být
(má být  ) má vlastnosti střední příčky, protože jsem její existenci již od začátku předpokládal. To ale opravdu není samozřejmost. Uvedl bych jeden příklad, kde by se opravdu jednalo o důkaz kruhem. Uvažujme tři různé body
) má vlastnosti střední příčky, protože jsem její existenci již od začátku předpokládal. To ale opravdu není samozřejmost. Uvedl bych jeden příklad, kde by se opravdu jednalo o důkaz kruhem. Uvažujme tři různé body  ,
,  ,
,  které leží v přímce
které leží v přímce  . Uvažujme, že je sestrojena kružnice, která všechny tyto tři body obsahuje. Uvažujme její střed
. Uvažujme, že je sestrojena kružnice, která všechny tyto tři body obsahuje. Uvažujme její střed  . Ten leží na kolmici k přímce
. Ten leží na kolmici k přímce  vedené středem úsečky
vedené středem úsečky  a také na kolmici k přímce
a také na kolmici k přímce  vedené středem úsečky
vedené středem úsečky 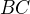 . Má tedy od všech tří bodů stejnou vzdálenost. Tím je dokázáno, že ke každým třem různých bodům ležícím v jedné přímce lze sestrojit jedinou kružnici, která všechny tyto tři body obsahuje. To je samozřejmě špatně, protože uvažovaný střed
. Má tedy od všech tří bodů stejnou vzdálenost. Tím je dokázáno, že ke každým třem různých bodům ležícím v jedné přímce lze sestrojit jedinou kružnici, která všechny tyto tři body obsahuje. To je samozřejmě špatně, protože uvažovaný střed  je imaginární. Nikde jsem si ho nesestrojil, pouze jsem předpokládal jeho existenci a řekl, jaké má vlastnosti. Něco jiného by ale bylo, kdybych řekl. "Ten leží na kolmici k přímce
je imaginární. Nikde jsem si ho nesestrojil, pouze jsem předpokládal jeho existenci a řekl, jaké má vlastnosti. Něco jiného by ale bylo, kdybych řekl. "Ten leží na kolmici k přímce  vedené středem úsečky
vedené středem úsečky  a také na kolmici k přímce
a také na kolmici k přímce  vedené středem úsečky
vedené středem úsečky 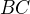 . Tyto dvě kolmice nemají žádný společný bod. Pro střed
. Tyto dvě kolmice nemají žádný společný bod. Pro střed  již v úvahu nepřipadá žádný další bod. Tím je dokázáno, že ke třem různým bodům, které leží v přímce, nelze sestrojit kružnici, která by všechny tyto tři body obsahovala.". A stejně tak i já jsem si sestrojil reálnou přímku
již v úvahu nepřipadá žádný další bod. Tím je dokázáno, že ke třem různým bodům, které leží v přímce, nelze sestrojit kružnici, která by všechny tyto tři body obsahovala.". A stejně tak i já jsem si sestrojil reálnou přímku  (má být
(má být  ) a dokázal na základě vlastností konstrukce, že je to střední příčka. Klidně by se mi mohlo stát, že by mi při důkazu pro přímku
) a dokázal na základě vlastností konstrukce, že je to střední příčka. Klidně by se mi mohlo stát, že by mi při důkazu pro přímku  již nevyšla žádná příčka, která by přicházela v úvahu(ani ta přímka
již nevyšla žádná příčka, která by přicházela v úvahu(ani ta přímka  ), potom bych udělal závěr, že neexistuje žádná střední příčka dvou mimoběžek
), potom bych udělal závěr, že neexistuje žádná střední příčka dvou mimoběžek  ,
,  . A jednalo by se o důkaz sporem.
. A jednalo by se o důkaz sporem.
Edit 15.7 21:10 - tady jsem to trochu opravil
Offline
#17 15. 09. 2011 15:29 — Editoval Rumburak (15. 09. 2011 17:28)
Re: Vzdálenost dvou mimoběžek - pomoc s důkazem
↑ pepa999:
Ahoj, bohužel pár dní teď nebudu mít tolik času, abych mohl podrobněji a hlavně v klidu prostudovat Tvůj poslední příspěvek. Nyní pouze uvedu
několik poznámek na téma důkaz.
Mnoho matematických vět, snad i většina, má tvar implikace
(1) 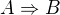 ,
,
kde  je výrok, jehož platnost se předpokládá (v našem případě "p, q jsou mimoběžky v trojrozměrném eukleidovském prostoru")
je výrok, jehož platnost se předpokládá (v našem případě "p, q jsou mimoběžky v trojrozměrném eukleidovském prostoru")
a  je výrok, jehož platnost se na základě předpokladu
je výrok, jehož platnost se na základě předpokladu  dokazuje (v našem případě "existuje přímka r, která každou z přímek p, q
dokazuje (v našem případě "existuje přímka r, která každou z přímek p, q
protíná kolmo").
Dokázat větu (1) lze několika způsoby :
I. Přímý důkaz spočívá v tom, že nalezneme konečný seznam výroků
(2) 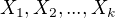
takových, aby byl splněn - zřejmě či na základě dílčího důkazu - každý z výroků 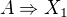 ,
,  , ...,
, ..., 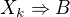 .
.
II. Nepřímé důkazy spočívají v tom, že místo výroku (1) dokazujeme nějaký výrok  , který je s výrokem (1) ekvivalentní.
, který je s výrokem (1) ekvivalentní.
Za výrok  bereme nejčastěji
bereme nejčastěji
buďto výrok 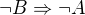 - někteři autoři pak hovoří o důkazu obměnou,
- někteři autoři pak hovoří o důkazu obměnou,
nebo výrok 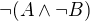 - zde hovoříme o důkazu sporem .
- zde hovoříme o důkazu sporem .
Důkaz obměnou je možno realisovat přímou cestou, jak popsáno výše. Důkaz sporem se provádí tak, že najdeme takový konečný seznam výroků
(3) 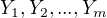 ,
,
aby byl splněn (zřejmě či na základě dílčího důkazu) každý z výroků 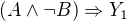 ,
, 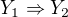 , ...,
, ..., 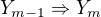 ,
, 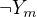 .
.
Shruba takovouto definici důkazu (snad vyjádřenou poněkud jinými výrazovými prostředky) bychom našli v učebnici zabývající se touto tematikou.
Dokazovat implikaci (1) tak, že místo ní dokážeme implikaci
(4) 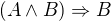 ,
,
je od začátku špatně , protože výrok (4) je platný vždy (je to tautologie) , a to i tehdy, když by výroky B, (1) platné nebyly, takže z úspěšného
důkazu výroku (4) nemůžeme o platnosti výroku (1) usuzovat vůbec nic. Předpoklad "nechť B" v souvislosti s důkazem věty (1) patří nanejvýše
do nějakých předběžných úvah, které by ale od důkazu věty (1) měly být jasně odděleny a tento důkaz by na ně neměl nijak navazovat.
Ona hranice mezi těmi předběžnými úvahami a vlastním důkazem věty není v Tvém prvním důkaze nijak vyznačena. Ale pro klid svého svědomí
se na ten první i poslední důkaz ještě podívám a pokusím se ji nalézt - až bude na to více klidu. Rozhodně nejsou tak průhledné jako ten v pořadí
druhý, ve kterém si předpokladem "nechť B" nevypomáháš.
EDIT. Ještě doplnim, že důkaz kruhem se nemusí týkat jen nepravdivých tvrzení. Například "dokazujme" platný vzorec
(5) 
pro obsah rovnostranného trojúhelníka o straně délky  : Mějme takový rovnostranný trojúhelník a sestrojme v něm střední příčky.
: Mějme takový rovnostranný trojúhelník a sestrojme v něm střední příčky.
Ty nám rozdělí původní trojúhelník na čtyři shodné rovnostranné trojúhelníky, jejichž strany mají stejnou délku  a tudíž obsah
a tudíž obsah
každého z nich je 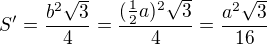 . Obsah celého původního trojúhelníka tedy bude
. Obsah celého původního trojúhelníka tedy bude
 .
.
To, že závěrečné tvrzení je správné, ještě neznamená, že byl důkaz správně veden.
EDIT 2 . Něco z Tvého posledního příspěvku jsem přece jen prostudoval - připojuji své komentáře barevně
pepa999 napsal(a):
Pokusím se ti teď popsat, proč si ještě pořád myslím, že je můj důkaz správně: ... A ten důkaz opravdu závisí na existenci té střední příčky, to nepopírám. Je to totiž úvaha pro případ, že střední příčka existuje a někdo ji sestrojí. Co je na tom špatného? Že důkaz existence střední příčky závisí na předpokladu existence téže střední příčky, to je přesně ta chyba. Na konci důkazu tedy vím, že buď střední příčka neexistuje, nebo je to příčka
. Přesně toto "jsi věděl" od chvle, kdy ses rozhdl případnou střední příčku označít
, tedy hned od začátku. ... Na konci důkazu jsem si ještě dokázal z vlastností konstrukce, že příčka
je střední příčkou Bylo by tristní, kdyby takový důkaz nevyšel, když jsi platnost dokazovaného tvrzení předpokládal.******
Offline
#18 15. 09. 2011 20:55 — Editoval pepa999 (16. 09. 2011 11:37)
Re: Vzdálenost dvou mimoběžek - pomoc s důkazem
Rumburak napsal(a):
EDIT 2 . Něco z Tvého posledního příspěvku jsem přece jen prostudoval - připojuji své komentáře barevně
pepa999 napsal(a):
Pokusím se ti teď popsat, proč si ještě pořád myslím, že je můj důkaz správně: ... A ten důkaz opravdu závisí na existenci té střední příčky, to nepopírám. Je to totiž úvaha pro případ, že střední příčka existuje a někdo ji sestrojí. Co je na tom špatného? Že důkaz existence střední příčky závisí na předpokladu existence téže střední příčky, to je přesně ta chyba. Na konci důkazu tedy vím, že buď střední příčka neexistuje, nebo je to příčka
. Přesně toto "jsi věděl" od chvle, kdy ses rozhdl případnou střední příčku označít
, tedy hned od začátku. ... Na konci důkazu jsem si ještě dokázal z vlastností konstrukce, že příčka
je střední příčkou Bylo by tristní, kdyby takový důkaz nevyšel, když jsi platnost dokazovaného tvrzení předpokládal.******
Omlouvám se, uvědomuji si, co jsem udělal za chybu. Ne přímo v důkazu, tam tu sestrojenou příčku neoznačuji nijak(úplně v tom prvním). Ale když se na ten důkaz odkazuji, označuji ji stejně jako tu předpokládanou, takže všechna ta tvrzení jsou tautologiemi, a chápu, že k těm ani žádné důkazy mít nemusím. Ale mělo to být jinak. Určitě pochopíš, co přesně za chybu teď mám na mysli, když ti řeknu, že z mého prvního důkazu plyne: Jestliže existuje střední příčka  (teď už
(teď už  ) mimoběžek
) mimoběžek  ,
,  , potom
, potom  (teď už
(teď už  ) =
) =  .(Kde
.(Kde  je ta nalezená a skutečně sestrojená přímka). Následně z vlastností konstrukce dokazuji, že
je ta nalezená a skutečně sestrojená přímka). Následně z vlastností konstrukce dokazuji, že  je střední příčka.
je střední příčka.
Rumburak napsal(a):
EDIT. Ještě doplnim, že důkaz kruhem se nemusí týkat jen nepravdivých tvrzení. Například "dokazujme" platný vzorec
(5)
pro obsah rovnostranného trojúhelníka o straně délky: Mějme takový rovnostranný trojúhelník a sestrojme v něm střední příčky.
Ty nám rozdělí původní trojúhelník na čtyři shodné rovnostranné trojúhelníky, jejichž strany mají stejnou délkua tudíž obsah
každého z nich je. Obsah celého původního trojúhelníka tedy bude
.
To, že závěrečné tvrzení je správné, ještě neznamená, že byl důkaz správně veden.
S tímto také naprosto souhlasím. Vidím tam tu zřejmou tautologii: Jestliže bude mít trojúhelník takový obsah, potom bude mít takový obsah. Ale řekl bych, že toto je něco jiného, protože ty skutečný trojúhelník nemáš. Já jsem odvodil, čím ta přímka bude. Skutečnou sestrojenou přímkou  , kterou si mohu osahat. A kterou následně zkoumám, abych zjistil, jestli skutečně splňuje to, co chceme.
, kterou si mohu osahat. A kterou následně zkoumám, abych zjistil, jestli skutečně splňuje to, co chceme.
Uvedl bych jeden příklad, který ukáže, že se v mém důkazu opravdu nejedná o tautologii(když pominu tu chybu, se kterou jsem se na ten důkaz odkazoval. V samotném důkazu jsem tuto chybu ale neudělal, nalezenou přímku jsem nijak nepojmenoval) a že takový důkaz opravdu nemusí vždy vyjít.
Mějme kosočtverec  ,
,  ,
,  ,
,  s úhlem při vrcholu
s úhlem při vrcholu  15°. Uvažujme, že je sestrojena kružnice, která obsahuje všechny jeho vrcholy. Nyní uvažujme její střed, označme ho
15°. Uvažujme, že je sestrojena kružnice, která obsahuje všechny jeho vrcholy. Nyní uvažujme její střed, označme ho  . Víme, že střed
. Víme, že střed  leží na kolmici k přímce
leží na kolmici k přímce  vedené středem úsečky
vedené středem úsečky  . A také na kolmici k přímce
. A také na kolmici k přímce 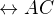 vedené středem úsečky
vedené středem úsečky 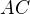 . Označme průsečík těchto dvou kolmic
. Označme průsečík těchto dvou kolmic  (ten existuje a já si ho sestrojím. Nebudu dokazovat, že existuje, je to pro účely tohoto příkladu zbytečné). Střed
(ten existuje a já si ho sestrojím. Nebudu dokazovat, že existuje, je to pro účely tohoto příkladu zbytečné). Střed  se tedy rovná
se tedy rovná  . Právě jsem dokázal, že: Jestliže existuje kružnice, která obsahuje všechny vrcholy trojúhelníku
. Právě jsem dokázal, že: Jestliže existuje kružnice, která obsahuje všechny vrcholy trojúhelníku  ,
,  ,
,  ,
,  , potom pro její střed
, potom pro její střed  platí:
platí:  =
=  . Bod
. Bod  jsem si skutečně sestrojil a teď s ním budu pracovat. Dokážu, že neleží na kolmici k přímce
jsem si skutečně sestrojil a teď s ním budu pracovat. Dokážu, že neleží na kolmici k přímce 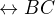 vedené středem úsečky
vedené středem úsečky 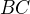 . A tedy, neexistuje kružnice se středem v bodě
. A tedy, neexistuje kružnice se středem v bodě  , která by obsahovala všechny vrcholy kosočtverce
, která by obsahovala všechny vrcholy kosočtverce  ,
,  ,
,  ,
,  (bod
(bod  má od tří vrcholů různé vzdálenosti). A díky dříve dokázané implikaci také vím, že neexistuje vůbec žádná kružnice, která by obsahovala všechny vrcholy kosočtverce
má od tří vrcholů různé vzdálenosti). A díky dříve dokázané implikaci také vím, že neexistuje vůbec žádná kružnice, která by obsahovala všechny vrcholy kosočtverce  ,
,  ,
,  ,
,  .
.
EDIT: Tento typ důkazu bych označil za shodný s typem mého prvního důkazu. Také bych rád napsal jeho verzi, typově shodnou s poslední verzí mého důkazu, ale nebudu nic předpokládat. A opět bude podle mého názoru platit, že řeknu pouze jinými slovy to, co říkám tady v té první verzi důkazu s kosočtvercem.
Mějme kosočtverec  ,
,  ,
,  ,
,  s úhlem při vrcholu
s úhlem při vrcholu  15°. Uvažujme libovolnou kružnici se středem
15°. Uvažujme libovolnou kružnici se středem  , který neleží na kolmici k přímce
, který neleží na kolmici k přímce  vedené středem úsečky
vedené středem úsečky  , nebo neleží na kolmici k přímce
, nebo neleží na kolmici k přímce 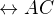 vedené středem úsečky
vedené středem úsečky 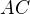 . Označme průsečík těchto dvou kolmic
. Označme průsečík těchto dvou kolmic  . Taková kružnice má střed vzdálený různě od alespoň dvou různých bodů kosočtverce
. Taková kružnice má střed vzdálený různě od alespoň dvou různých bodů kosočtverce  ,
,  ,
,  ,
,  , neobsahuje proto všechny tyto body. V úvahu už připadají pouze kružnice, jejichž střed leží na kolmici k přímce
, neobsahuje proto všechny tyto body. V úvahu už připadají pouze kružnice, jejichž střed leží na kolmici k přímce  vedené středem úsečky
vedené středem úsečky  . A také na kolmici k přímce
. A také na kolmici k přímce 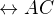 vedené středem úsečky
vedené středem úsečky 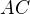 . A tedy se středem
. A tedy se středem  =
=  . Uvažujme libovolnou takovou kružnici. Její střed
. Uvažujme libovolnou takovou kružnici. Její střed  neleží na kolmici k přímce
neleží na kolmici k přímce 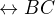 vedené středem úsečky
vedené středem úsečky 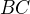 a tedy má od bodů
a tedy má od bodů  ,
,  různé vzdálenosti a proto žádná kružnice se středem v bodě
různé vzdálenosti a proto žádná kružnice se středem v bodě  neobsahuje všechny body kosočtverce
neobsahuje všechny body kosočtverce  ,
,  ,
,  ,
,  . Tím je dokázáno, že neexistuje žádná kružnice, která by obsahovala všechny vrcholy kosočtverce
. Tím je dokázáno, že neexistuje žádná kružnice, která by obsahovala všechny vrcholy kosočtverce  ,
,  ,
,  ,
,  .
.
Rumburak napsal(a):
Ale pro klid svého svědomí se na ten první i poslední důkaz ještě podívám a pokusím se ji nalézt - až bude na to více klidu. Rozhodně nejsou tak průhledné jako ten v pořadí druhý, ve kterém si předpokladem "nechť B" nevypomáháš.
V tom úplně posledním si již také žádným předpokladem nevypomáhám. Chtěl jsem udělat verzi, ve které bych si ničím nevypomáhal a nejenže dokázal existenci jedné střední příčky, ale hned v tom jednom také neexistenci dalších středních příček.
Offline
#19 15. 09. 2011 21:04 — Editoval pepa999 (16. 09. 2011 20:24)
Re: Vzdálenost dvou mimoběžek - pomoc s důkazem
Jak si to tak čtu, co jsem všechno napsal, tak jsem to psal dost zmateně. Neoznačil jsem si vůbec tu nalezenou přímku a potom jsem ji označoval jako tu předpokládanou, přitom jsem měl ale pořád na mysli tu nalezenou, takže za to se omlouvám. Pokusím se to všechno opravit.
EDIT: I když, to by v tom byl ještě větší zmatek, protože jsi na mě dost často reagoval, takže chtěl bych teď označit tu nalezenou přímku jako  . A také ve všech tautologických větách, kde jsem použil písmeno
. A také ve všech tautologických větách, kde jsem použil písmeno  , mělo být písmeno
, mělo být písmeno  .
.
EDIT2: V příspěvku, kde jsem napsal poslední verzi mého důkazu, jsem barevně vyznačil změny. V předchozích příspěvcích to prostě mělo být  taky.
taky.
EDIT3: Teď už jsem to celé pochopil... Ve druhé verzi mého důkazu(kde jsem nic nepředpokládal) jsem označil tu přímku, o které jsem dokázal, že je střední příčka, jako  a to byla ta chyba, protože už od té doby byly všechny moje příspěvky nepřehledné. Rozhodl jsem se, že všechno barevně opravím tak, aby to bylo zřetelnější...
a to byla ta chyba, protože už od té doby byly všechny moje příspěvky nepřehledné. Rozhodl jsem se, že všechno barevně opravím tak, aby to bylo zřetelnější...
EDIT4: Tak už jsem to všude opravil. V každém důkazu tu předpokládanou střední příčku(pokud tam něco předpokládám) označuji jako  a tu sestrojenou přímku označuji ve všech důkazech jako
a tu sestrojenou přímku označuji ve všech důkazech jako  .
.
Offline
#20 16. 09. 2011 15:05 — Editoval Rumburak (16. 09. 2011 15:26)
Re: Vzdálenost dvou mimoběžek - pomoc s důkazem
↑ pepa999:
Po Tvých posledních příspěvcích se kloním k názoru, že problematice rozumíš, a že tu jde spíše jen o trochu té rutiny v důkazové technice.
V Tvém prvním důkazu se po posledních jeho úpravách lépe orientuji a asi jsem už konečně pochopil podstatu problému: důkaz existence
a důkaz jednoznačnosti se navzájem poněkud prolínají, což je na úkor přehlednosti. Přehlednější by bylo důkaz adekvátně rozdělit na dvě
samostatné části, u důkazů tohoto druhu se to tak i běžně praktikuje. Náznak, kterým směrem se ta která část bude ubírat, autora nestojí
téměř nic a čtenáři velmi pomůže (Nejprve dokážeme existenci. .... Nyní dokážeme jednoznačnost. ...) Rovněž se vyplatí dokazovanou větu
předem ještě přesně zformulovat, zvláště pokud je složitější, což ale nebyl náš případ.
Offline
#21 16. 09. 2011 20:40
Re: Vzdálenost dvou mimoběžek - pomoc s důkazem
↑ Rumburak:
Ano, je to přesně tak, důkaz jednoznačnosti a existence dělám vlastně najednou a omlouvám se, že jsem přehlednosti nevěnoval příliš pozornost.
Jinak děkuji za rady ohledně zkvalitnění důkazu.
Offline
Stránky: 1
- Hlavní strana
- » Střední škola
- » Vzdálenost dvou mimoběžek - pomoc s důkazem (TOTO TÉMA JE VYŘEŠENÉ)
