Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 13. 09. 2011 23:01
Geometrické zobrazenia
Dobrý večer,
mám problém s nasledujúcou úlohou:
V rovině je dána přímka p a mimo ni dva různé body A,B. Sestrojte na přímce p bod X tak, aby odchylka přímky AX od přímky přímky p byla dvojnásobkem odchylky přímky BX od přímky p.
Nedarí sa mi pri tejto úlohe dobre popísať bod X vlastnosťami na základe, ktorých by som ho vedel zostrojiť.(akurát viem, že bod X musí ležať na priamke B´X ,kde B´ je obrazom B v osovej symetrii podľa p, ale iný bod tej priamky neviem nájsť a tiež sa mi nedarí využiť vlastnosť bodu A) Prosím o malý hint. Ďakujem
Offline
#3 15. 09. 2011 18:28
- check_drummer

- Příspěvky: 4900
- Reputace: 105
Re: Geometrické zobrazenia
Bod X najdeme výpočtem:
Kolmý průmět A(B) na p označíme C(D). Předpokládejme, že neznámý bod X leží mezi C a D (případy, kdy tomu tak není vyřešíme analogicky). Pak za pomoci délek CD,AC,BD a sestrojme soustavu rovnic s neznámou x(=CX) a  , kde
, kde  je úhel DXB, pak úhel CXA je
je úhel DXB, pak úhel CXA je  a vztah pro tangens obou úhlů dá dvě rovnice. Použijeme vzorec pro dvojnásobný argument funkce tan, dosadíme z první rovnice
a vztah pro tangens obou úhlů dá dvě rovnice. Použijeme vzorec pro dvojnásobný argument funkce tan, dosadíme z první rovnice 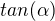 do druhé, získáme tak kvadratickou rovnici, vyřešíme a výsledek "sestrojíme".
do druhé, získáme tak kvadratickou rovnici, vyřešíme a výsledek "sestrojíme".
Není to sice elegantní, ale řešení to je. :-)
"Máte úhel beta." "No to nemám."
Offline
#4 16. 09. 2011 19:03
Re: Geometrické zobrazenia
↑ check_drummer:
ďakujem aj za tento postup, ale mňa skôr zaujíma geometrické riešenie. Ono by sa to malo dať riešiť cez geometrické zobrazenia.
Offline
#5 17. 09. 2011 11:36
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Geometrické zobrazenia
Zdravím,
↑ check_drummer:
tuto úlohu jsi jednou odkázal k nezdaru :-). Analyticky mi také vychází řešitelná a sestrojitelná (jako konstrukce výrazu), ovšem geometricky mi to nejde - zkoušela jsem kombinovat s dalším zobrazením, využit vlastnost, kde se objevuje poloviční úhel (středový a obvodový úhel, původní bod B leží na ose úhlu  , když doplním, otočení přímky p).
, když doplním, otočení přímky p).
Alan122 napsal(a):
akurát viem, že bod X musí ležať na priamke B´X ,kde B´ je obrazom B v osovej symetrii podľa p, ale iný bod tej priamky neviem nájsť a tiež sa mi nedarí využiť vlastnosť bodu A) Pro
tato vlastnost by se využila, pokud máme zajistit, že úhel dopadu (z bodu A) má být stejný jako úhel odrazu (do bodu B), zde se mi zdá, že nejdřív musí být posun bodu B a až potom využití osové souměrnosti.
Bohužel, do 5 minut úvah jsem nic nevymyslela, tedy další úvahy u mne v úvahu nepřicházejí (případně ještě se podívat v okolí zdroje úlohy, to už jsem nezkoušela). Přesunu vám to do Zajímavých SŠ, třeba si toho někdo z kolegů všimne. Děkuji, ať se podaří.
Offline
#6 17. 09. 2011 15:18 — Editoval Kondr (17. 09. 2011 15:48)
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Geometrické zobrazenia
Protne-li AB přímku p vbodě C, vzpomeneme na známourovnost XA:XB=CB:BA a na Apollóniovu kružnici. Edit: neprotne-li tak vezmeme limitní případ té Apolloniovy kružnice (střed v A, poloměr |AB|).
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#7 17. 09. 2011 15:30
Re: Geometrické zobrazenia
Moje pozorovanie.
Ak sú A, B v rôznych polrovinách s hraničnou priamkou "p", tak zostrojíme kružnicu so stredom B a polomerom |BA|. Priesečníky s priamkou "P" označme C, D. Zostrojme osí úsečiek CA, CD. Priesečníky s "p" sú X, X'. Jeden z tých bodov má požadovanú vlastnosť, ale nie úplne, pretože niekedy je "180 - odchylka AX od p" / 2 rovná odchylke "BX" od "p", čo ale nechceme a neviem, ako tento prípad ošetriť.
1^6 - 2^6 + 3^6 = 666
Offline
#8 17. 09. 2011 21:24
- check_drummer

- Příspěvky: 4900
- Reputace: 105
Re: Geometrické zobrazenia
jelena napsal(a):
Zdravím,
↑ check_drummer:
tuto úlohu jsi jednou odkázal k nezdaru :-).
Tak to se omlouvám. :-) Avšak to byla jen domněnka, nikoli podložené tvrzení - která neměla auora otázky zcela odradit. :-)
"Máte úhel beta." "No to nemám."
Offline
#9 26. 09. 2011 19:30
Re: Geometrické zobrazenia
Offline
#10 04. 10. 2011 11:46
Re: Geometrické zobrazenia
↑ Alan122:
Případ, kdy body A, B nejsou odděleny přímkou p: Vyčerpávající řešení nemám, jen nápovědu.
Bod X volíme tak, aby přímky p, XA byly souměrné podle osy XB. Ale možná že ne vždy to půjde .
Offline