Matematické Fórum

etchie · 17. 09. 2011 21:18

trapim sa s touto rovnicou:

$cos(x+\frac{\pi}{3})=sin(3x)$

po upravach dostanem:

$\frac{1}{2}(cosx-\sqrt{3}sinx)=3sinx-4sin^3x$

co este ide upravit na
$cosx=6sinx-8sin^3x+\sqrt{3}sinx$
ale dalsimi upravami to nikam nevedie...
poradite nejaky trik ?

dakujem

((:-)) · 17. 09. 2011 21:38 — Editoval ((:-)) (18. 09. 2011 12:11)

↑ etchie:

Stroj (WA) vyriešil takto:

Odkaz

ale vzdávať sa netreba... :-)

V druhom riadku je vidno, že využili rovnosť $\cos\alpha = \sin $\frac{\pi}{2}-\alpha$$ .

Po dosadení do Tvojej rovnice dostaneš tvar sin... = sin... , čo sa po prenesení sinusov na jednu stranu a využití vzťahu pre rozdiel sinusov asi už dá vyrátať ...

etchie · 18. 09. 2011 11:36

↑ ((:-)):

stale to nejako nevidim

prevediem teda lavu stranu podla toho vzorca na
$cos(x+\frac{\pi}{3})<=>sin(\frac{\pi}{6}-x)$

a z toho
$3sinx-4sin^3x-sin(\frac{\pi}{6}-x)=0$
a teraz prevod na sucinovy tvar ?
viem s tym urobit akurat tak
$2sinx-4sin^3x+sinx-sin(\frac{\pi}{6}-x)=0$ a ked aplikujem vzorec $sinx-siny=2sin(\frac{x+y}{2})cos(\frac{x-y}{2})$ a este vydelim 2, tak
$sinx-2sin^3x+cos\frac{\pi}{12}sin(x-\frac{\pi}{12})=0$
a zas to nikam nevedie :-(

((:-)) · 18. 09. 2011 11:39 — Editoval ((:-)) (18. 09. 2011 11:46)

↑ etchie:

Nie.

$\cos\alpha = \sin $\frac{\pi}{2}-\alpha$$

Hneď na začiatku prevedieš kosínus z ľavej strany podľa tohto vzťahu na sínus...

Sínus z pravej strany dáš na ľavú.

Existujú "vzorce" na rozdiel dvoch sinusov...

$\sin$\frac{\pi}{6}-x$=\sin(3x)$

etchie · 18. 09. 2011 14:10

↑ ((:-)):

aha, ok

takze
$sin(\frac{\pi}{6}-x)=sin3x\\ sin(\frac{\pi}{6}-x)-sin3x=0\\ 2cos(\frac{\pi/6-x+3x}{2})sin(\frac{\pi/6-x-3x}{2})=0\\ cos(\frac{\pi}{12}+x)sin(\frac{\pi}{24}-x)=0$

$cos(X)=0$ prave vtedy, ked $\frac{\pi}{12}+x=\frac{\pi}{2}$ alebo $sin(X)=0$ prave vtedy, ked $\frac{\pi}{24}-x=\pi$
z toho teda urcim, ze: $x_1=\frac{5}{12}\pi+k\pi$ a $x_2=\frac{\pi}{24}+k\pi$

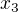existuje vsak aj koren $x_3=\frac{\pi}{24}+k\frac{\pi}{2}$ , ktory vyhovuje povodnej rovnici, ale k nemu sa neviem dopracovat. pravdepodobnu existenciu $x_3$ bolo vidno uz v predoslom rozklade $sin(3x)$ , kde sa objavila tretia mocnina, co by malo znamenat existenciu troch korenov

zdenek1 · 18. 09. 2011 14:33

↑ etchie:
4. řádek je špatně
$\cos\left(\frac\pi{12}+x\right)\sin\left(\frac\pi{12}-2x\right)=0$

etchie · 18. 09. 2011 14:57

↑ zdenek1:

dakujem

takze $sin\left(\frac\pi{12}-2x\right)=0$ prave vtedy ked $\frac\pi{12}-2x=0$ alebo $\frac\pi{12}-2x=\pi$
a odtial je $x_2=\frac{\pi}{24}$ a $x_3=\frac{\pi}{24}-\frac{\pi}{2}$
co mozem napisat ako spolocny druhy koren $x_2=\frac{\pi}{24}+k\frac{\pi}{2}$

zdenek1 · 18. 09. 2011 15:02

↑ etchie:
čistě technicky je jepší si tu periodu psát hned, takže
$\frac\pi{12}-2x=k\pi$
$2x=\frac\pi{12}-k\pi$
$x=\frac\pi{24}+k\frac\pi2$ (můžeš změnit znaménko u $k$ , protože probíhá všechna celá čísla, a je jedno jestli začne u $-\infty$ a směřuje do plusu, nebo obráceně.

etchie · 18. 09. 2011 15:13

↑ zdenek1:

presne toto som potreboval,
lebo casto vyriesim goniometricke rovnice "takmer" spravne - chyba v nich nejaka cast periody a teraz uz aj viem preco

dakujem vsetkym zucastnenym za pomoc s riesenim

Matematické Fórum

#1 17. 09. 2011 21:18

goniometricka rovnica

#2 17. 09. 2011 21:38 — Editoval ((:-)) (18. 09. 2011 12:11)

Re: goniometricka rovnica

#3 18. 09. 2011 11:36

Re: goniometricka rovnica

#4 18. 09. 2011 11:39 — Editoval ((:-)) (18. 09. 2011 11:46)

Re: goniometricka rovnica

#5 18. 09. 2011 14:10

Re: goniometricka rovnica

#6 18. 09. 2011 14:33

Re: goniometricka rovnica

#7 18. 09. 2011 14:57

Re: goniometricka rovnica

#8 18. 09. 2011 15:02

Re: goniometricka rovnica

#9 18. 09. 2011 15:13

Re: goniometricka rovnica

Zápatí