Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 17. 10. 2007 21:53 — Editoval Marian (17. 10. 2007 23:05)
Re: Sumy
Mas v postate dve moznosti, jak celou vec provest. Nebo spise ja mam dve moznosti (prinejmensim), jak celou vec matematicky korektne dokazat. Prvni moznost je vysvetlit, jak takove sumy pocitame, nebo druha moznost, nevysvetlovat nic, rici jaky je vysledek a dokazat obe vyrcena tvrzeni pomoci matematicke indukce. Prvni varianta mi pripada rozumnejsi. Vyjadrim se k ni nize.
Nejprve se vyjadrim k rade  .
.
Budu predpokladat, ze cislo  je je prirozene, tedy
je je prirozene, tedy 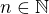 . Pouziva se v tomto pripade nejcasteji tzv. teleskopicke scitani. K tomu provedeme rozklad sumandu na parcialni zlomky:
. Pouziva se v tomto pripade nejcasteji tzv. teleskopicke scitani. K tomu provedeme rozklad sumandu na parcialni zlomky: . Proto mame
. Proto mame .
.
U rady  bude pocitani vice. Za timto ucelem vyresim situaci obecnejsi. Opet necht
bude pocitani vice. Za timto ucelem vyresim situaci obecnejsi. Opet necht 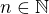 . Budeme pozorovat radu
. Budeme pozorovat radu ,
,
coz je funkce promenne x; proto definuju .
.
To je soucet prvnich n clenu geometricke posloupnosti. Navicpokud je  , soucet se snadno najde, totiz plati
, soucet se snadno najde, totiz plati .
.
Je-li 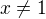 , najdeme vzorec pro soucet prvnich n clenu geometricke posloupnosti napriklad v tabulkach (dukaz delat nebudu). Plati tedy
, najdeme vzorec pro soucet prvnich n clenu geometricke posloupnosti napriklad v tabulkach (dukaz delat nebudu). Plati tedy
Pripad f(1)=n je pro nas nezajimavy -- ukaze se to pozdeji. Funkci f(x) nyni budeme derivaovat, tedy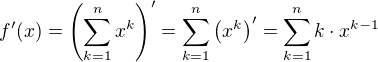 .
.
Z toho snadno plyne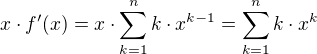 .
.
Na druhou stranu ale musi pro 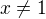 platit
platit  .
.
To vynasobim nyni x-em a porovnam s vyrazem 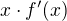 vyse. Proto
vyse. Proto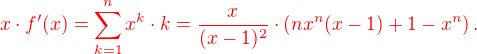
Konecne si staci vsimnout, ze hledana rada  neni nic jineho nez hodnota funkce
neni nic jineho nez hodnota funkce 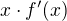 v bode
v bode 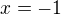 . Dosadis-li do cervene oznacene rovnice, mame uzavreny tvar konecneho souctu
. Dosadis-li do cervene oznacene rovnice, mame uzavreny tvar konecneho souctu  . Tudiz po upravach
. Tudiz po upravach .
.
Hotovo.
Offline
#5 17. 10. 2007 22:56 — Editoval Kondr (13. 06. 2008 13:44)
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Sumy
No jde se na to podívat i tak, že uzávorkuješ po sobě jdoucí členy. Je třeba to rozdělit na sudé a liché n
pro n=2t
(-1+2)+(-3+4)+...+(-(2t-1)+2t), což je t závorek, každá s hodnotou 1, výsledek je t=n/2
pro n=2t+1
(-1+2)+(-3+4)+...+(-(2t-1)+2t)+(-1)(2t+1), což je užitím předchozího výsledku t-(2t+1)=-t-1=-n/2-1/2
Jinak pokud bychom počítali ten Marianův obecnější příklad 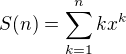 , stačí využít vztahů
, stačí využít vztahů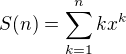
 ,
,
odečtením ,
,
odtud dokončíme pomocí vzorce pro geometrickou posloupnost.
@Marian: trik s derivací je pěkný, přidám do sbírky ;)
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#6 17. 10. 2007 22:57 — Editoval Marian (17. 10. 2007 23:04)
Re: Sumy
Tak me to napadlo proste. Bez derivaci je to sice mozne dokazat, ale hrabal bych se patrne asi jeste vice. Ale to reseni skutecne existuje. Vzpominam si na dva postupy, jak to provest bez derivace. Dnes to uz ale nechci hledat. Navic nekteri mne mohou popotahovat za vyse uvedeny postup, protoze jsem nedokazal vzorec pro soucet prvnich n clenu geometricke posloupnosti. Ale oni to urcite zkousnou.
Navic me jeste napada, ze by to slo snad uhadnout hypotezu, ja se chova ta zkoumana suma pomoci slabe indukce a vse by se pak muselo dokazat uplnou matematickou inducki. Ale to je loterie (to uhadnuti myslim). Reseni s derivaci je primejsi a ty derivace nejsou az tak tezke. Problemy muze pak snad cinit jeste sumacni znak, ale i to asi dlouho problem nebude.
Marian
[edit]
@ Kondr:
To je jeden z tech postupu, ktery jsem myslel.
===================================
@ jihos:
Lamu temer vsechny podobne veci pres derivace a integraly, klidne i v komplexni promenne. Sumy me proste bavi. Snad to nebylo na skodu a da se i ten muj postup pochopit.
PS: Vypocet jsem kontroloval jen zbezne. Pokud tam bude chyba, opravim pri prvni volne chvilce.
Offline