Matematické Fórum

Cipisek

Zdravím, chtel bych poprosit nekoho zdatneho na limity o opravu nasledujiciho prikladu. Diky.

A jeste tu mam jednu u u tejsem zatim uplne ztraceny :

kaja.marik

ad 1: rychly pohled rika ze asi O.K. Az na chybejici zavorky ve druhem kroku.

EDITACE: tak ten muj pohled byl opravdu hooooodne rychly, diky Marianovi za upresneni.

ad 2: $\lim_{a\to\infty}\frac{a}{a+1}\cdot \lim_{a\to\infty}\frac{\sqrt[3]{a^2}\sin(a!)}{a}$
ve druhem zlomku pokratit a vyuzit toho ze sinus je ohraniceny
------------------------------------
Rozběhli se k lesovně. Paní viděla je už z dálky. Věru, měla Káju skoro tak ráda jako Zdeňu.
Vždy? on to je, který ji naučil všecko s chutí sníst, který ji otužuje tak jako teď. Kájovi se houpají
v ruce svázané Zdeniny střevíčky a ona utíká skoro stejně rychle jako on.

Marian · 22. 06. 2008 20:39

↑ Cipisek:

ad 1. Plati sice zapis

$\lim_{a\to\infty}\frac{1}{\sqrt{a+1}+\sqrt{a}}=\lim_{a\to\infty}\frac{a\cdot\frac{1}{a}}{a\sqrt{1+\frac{1}{a}}+\sqrt{1}},$
ale neplati (pro vsechna realna cisla a, jez ma smysl dosadit)
$\frac{1}{\sqrt{a+1}+\sqrt{a}}=\frac{a\cdot\frac{1}{a}}{a\sqrt{1+\frac{1}{a}}+\sqrt{1}}.$

Ma byt spravne (chapu-li spravne hlavni myslenku strategie vypoctu autora)
$\frac{1}{\sqrt{a+1}+\sqrt{a}}=\frac{\sqrt{a}\cdot\frac{1}{\sqrt{a}}}{\sqrt{a}\cdot\left (\sqrt{1+\frac{1}{a}}+\sqrt{1}\right )}.$

ad 2. Zajimalo by me celkem, zda-li se jedna o limitu realne posloupnosti nebo realne funkce. Pokud jsou to funkce, je zapotrebi alespon vedet, jak je definovan vyraz $a!$ , tedy pomoci "Eulerova" integralu. Pro ty, kteri nevedi, jak je toto definovano, chci pouze upozornit, ze by kdosi take mohl klidne napsat, ze limita neexistuje, nebot vyraz "a!" neni znam. Pokud je ale definice znama, vyuzije se toho, co pise pan Marik.

Navic nelze obecne tvrdit, ze limita funkce (kde promenna (zde a) roste nade vsechny meze) se rovna limite (cislene) posloupnosti, kde promenna indexove mnoziny roste nade vsechny meze.

Cipisek · 23. 06. 2008 10:32

Dik. No snad to z toho nejak pochopím:/....
Jeste bych mel jednu otazuku k limitam. Nevite nekdo prosim jaky je rozdil v tom pokud je limita zadana:
1)

2)

... je mozne zadani 2) prepsat ne zpusob zadani 1)?

halogan

Je to aritmeticka posloupnost.

$a_1 = \frac{1}{a^2} \nl a_n = \frac{a-1}{a^2} \nl d = \frac{1}{a^2} \nl n = a - 1 \nl \nl s_n = \frac{n}{2}\cdot (a_1 + a_n) \nl s_n = \frac{n}{2}\cdot (\frac{1}{n^2} + \frac{a-1}{a^2}) \nl s_n = \frac{a-1}{2} \cdot \frac{a}{a^2} \nl s_n = \frac{a - 1}{2a}$

Cipisek · 23. 06. 2008 13:51

↑ halogan:
A pokud se pocita limita u te aritmeticke posloupnosti tak je to stejne jako pocitat limitu n-teho clenu?

halogan · 23. 06. 2008 13:58

To ne, protoze n-ty clen je proste jeden clen, tady ti jde o limitu toho souctu.

Marian · 24. 06. 2008 00:21 — Editoval Marian (24. 06. 2008 00:24)

↑ Cipisek:

Nehcapu presne vyznam tveho spojeni "prepsat na zpusob". Poprosil bych presnejsi vyjadrovani. Neni mozne odpovedet, neni-li presne znamo, co tazatel mini, i kdzy se to domnivam. Navic u druheho prikladu/ulohy by se hodila okrouhla zavorka, at je to uplne jednoznacne. Tak tolik k drobnostem.

Ted k tem horsim skrytym "zlům".

↑ halogan:
Nepises, co je aritmeticka posloupnost (kterou si chtel pravdepodobne zadat prvnim clenem - s tim souhlasim - a obecnym clenem - s tim nesouhlasim). Problem je v tom, ze promenna posloupnosti je zde oznacena jako a, pricemz a-ty clen by ve tvem podani musel vypadat jako $a_a$ . Sam posud, ze to neni vhodne. Navic motas a a n. Musis pouzit jine oznaceni pro posloupnost, treba 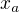$x_a$ , kde a je index. Potom

$x_1:=\frac{1}{a^2}\qquad\mathrm{a}\qquad x_a:=\frac{a}{a^2},\quad\forall a\in\mathbb{N}.$

Dale pak soucet

$\frac{1}{a^2}+\frac{2}{a^2}+\cdots +\frac{a-1}{a^2}=x_1+x_2+\cdots +x_{a-1}=\frac{a-1}{2}\left (x_1+x_{a-1}\right )=\frac{a-1}{2a}.$

Ale i tato varianta zapisu neni uplne v poradku formalne, protoze x_1 zavisi na a, stejne jako clen x_a.

Myslenka k reseni ulohy se da u tebe jasne detekovat a je spravna, ale se zapisem to je horsi.

Radsi bych to udelal tak, ze pisu

$y_a:=\frac{1}{a^2}+\frac{2}{a^2}+\cdots +\frac{a-1}{a^2}, \qquad\forall a\in\mathbb{N}.$

Pak

$y_a=\frac{1}{a^2}\cdot\left (1+2+\cdots +(a-1)\right )=\frac{1}{a^2}\cdot\frac{a-1}{2}\cdot a=\frac{a-1}{2a}.$

Zbytek je urcite jasny.

:-)

halogan · 24. 06. 2008 08:25

↑ Marian:

Ja to bral jako prvni clen (a_1) a posledni clen, jehoz index vsak neznam (a_n), ne clen obecny. Mel jsem asi spravne uvest a_(a-1), kde by vsak kolidovala pismenka a. Coz koliduji v celem mem reseni :)

Takze postupuji se spatnym zapisem, ale spravnym resenim :)

Matematické Fórum

#1 22. 06. 2008 17:38 — Editoval Cipisek (22. 06. 2008 18:27)

Limity

#2 22. 06. 2008 19:40 — Editoval kaja.marik (22. 06. 2008 21:22)

Re: Limity

#3 22. 06. 2008 20:39

Re: Limity

#4 23. 06. 2008 10:32

Re: Limity

#5 23. 06. 2008 12:22 — Editoval halogan (23. 06. 2008 12:25)

Re: Limity

#6 23. 06. 2008 13:51

Re: Limity

#7 23. 06. 2008 13:58

Re: Limity

#8 24. 06. 2008 00:21 — Editoval Marian (24. 06. 2008 00:24)

Re: Limity

#9 24. 06. 2008 08:25

Re: Limity

Zápatí