Matematické Fórum

xy2000 · 23. 06. 2008 14:18 — Editoval xy2000 (23. 06. 2008 14:18)

Vždy jsou správná právě dvě. Moc děkuji za odpovědi.

sneakfast · 23. 06. 2008 15:13

Ahoj, u prvního obrázku myslím, že správně je b) a c).

xy2000 · 23. 06. 2008 19:08

Vidím, že mi asi nikdo nepomůže :-(

Zkusil jsem se to vyřešit sám ,ale nevím zda-li je to dobře :-/

halogan · 23. 06. 2008 19:41

↑ xy2000:

V prvnim priklade je a) spatne a b) je spravne.

xy2000 · 23. 06. 2008 21:02

↑ halogan: a další příklady nevíte ?

sneakfast

↑ halogan: v prvním příkladě by e) nemělo být správně?

možná bereš jako inflexi i případ, kdy f'''(x)=0? my brali jako nutnou podmínku třetí derivaci nerovnou nule

halogan · 24. 06. 2008 00:05

↑ sneakfast:

O e) nevim. Ja jsem si jen skoro naprosto jisty ohledne tvrzeni o a) a b). Tot vse.

Marian · 24. 06. 2008 01:13 — Editoval Marian (08. 08. 2008 00:37)

↑ xy2000:

1. serie
(a) spatne (je-li funkce rostouci, derivace vubec nemusi existovat);
(b) spravne (plyne z konvergence posloupnosti (1+1/n)^n);
(c) spravne;
(d) spatne;
(e) spatne (napr. funkce f(x)=x^4 v bode x=0 nema inflexi, ale plnuje uvedene predpoklady).
_____________________________________

2. serie

(a) spatne (uvazime napr. mnozinu $M:=\left\{ x\in\mathbb{R};\, x=\frac{1}{n},\, \forall n\in\mathbb{N}\right\}$ . Tato je zdola omezena (napr. nulou), ale minimum neexistuje - existuje pouze infimum a plati $\inf M=0$ );
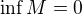(b) spatne (napr. funkce f(x):=0 ma derivaci spojitou, presneji f'(x)=0, ale f(x) neni ryze monotonni (je totiz konstantni));
(c) spatne (viz 1e);
(d) spravne (z definice extremu);
(e) spravne (neni receno, o jakou limitu se jedna (tedy jestli o vlastni nebo nevlastni). Mohou nastat celkem tri pripadz pro aritmetickou posloupnost: (i) konstantni => existuje limita vlastni, (ii) klesajici => limita je nevlastni -oo, (iii) rostouci => analogicky jako v (ii));
_____________________________________

3. serie

(a) spatne (napr. funkce f(x)=0 splnuje f(x)=-|f(x)|, ale neni prosta - je konstantni);
(b) spatne (napr. geometricka posloupnost dana jako a_1:=1, q=-1 je oscilujici, limita neexistuje);
(c) spravne;
(d) spravne;
(e) spatne (totiz po uprave a_n=n+1; posloupnost tedy diverguje);
_____________________________________

4. serie

(a) spatne (napr. f(x):=x^3);
(b) neuplne;
(c) spatne (viz 3b);
(d) spravne (funkce tam totiz roste);
(e) spravne;
_____________________________________

5. serie

(a) spravne (viz hlavni veta o monotonnich ciselnych posloupnostech);
(b) spatne (napr. funkce f(x):=sgn(x) a g(x)=-sgn(x) => f(x)+g(x)=0, coz je funkce spojita v bode x=0, ackoliv f(x) i g(x) jsou nespojite v bode x=0);
(c) spravne (ctu-li to spravne, tedy ze f(x):=|x|/x. Plati napr. -2<f(x)<2);
(d) spatne (jestlize f'(x)=1, pak f(x)=x+C. Pokud by platilo f(2)<f(1), bylo by to ekvivalantni 2+C<1+C, odkud 2<1, SPOR!);
_____________________________________

6. serie

(a) spatne (staci spocitat v bode x=1 jednostranne limity, napr. pomoci l'Hospitalova pravidla);
(b) spatne (napr. funkce sgn(x), ale nikoliv invertibilni na maximalnim definicnim oboru);
(c) spatne (viz 2e(ii) a 2e(iii));
(d) spravne;
(e) spravne;
_____________________________________

7. serie

(a) spravne (EDIT "za predpokladu, ze existuje prvni derivace f'(x) na uvedenem intervalu");
(b) spatne (nemusi dokonce existovat derivace vubec, natoz schavalit, ze existuje a rovna se nule);
(c) spatne (napr. f(x):=x^3);
(d) spatne (napr. f(x):=x^4);
(e) sravne (plyne z existence vlastni limity uvazovane posloupnosti);
(f) sparvne (jestlize totiz x=3.14 => x=314/100, coz je jiste racionalni cislo, tedy prvek mnoziny Q);
_____________________________________

8. serie

(a) |
(b) |
(c) > NECITELNE
(d) |
(e) |
_____________________________________

9. serie

(a) spatne (funkce prosta muze byt monotonni, ale take nemusi byt; nelze tedy obecne psat zaver, ze funkce prosta neni monotonni);
(b) spravne (viz 6e);
(c) spravne (viz 6d);
(d) spatne;
(e) spatne (staci spocitat jednostranne limity, ktere vyjdou vlastni).
_____________________________________

Poznamky.

(1) Ta zadani jsou na mnoha mistech nejasna. Neni mi vubec jasne, co autor techto dotazu mini pojmem limita. Lze tedy obe moznosti, a to vlastni i nevlastni.
(2) Definujeme-li posloupnost, je zapotrebi ucinit nekolik kroku k tomuto ucelu. Totiz tyto:
(a) definovat n-ty clen obecne,
(b) definovat indexovou mnozinu.
Toto jednoznacne chybi. Neni tedy vubec jasne, zda se jedna o posloupnosti konecne ci nekonence a neni tedy zajistena smysluplnost pojmu konvergence.
(3) V serii 1e je spatne odsazeni. Text je prilis vlevo, tedy blizko "cislovani" druhe urovne.
(4) Sekce 7 v puvodnim prispevku je praktickou ukazkou toho, jak nema vypadat matematicky text!

Marian · 24. 06. 2008 08:54

↑ halogan:

Co to znamena "skoro naprosto jisty"? Pripada mi to, jako by se reklo, ze nejaka zena je "tak trochu tehotna".

:-)

xy2000 · 24. 06. 2008 10:42

Děkuji za odpovědi, ale pořád si nejsem jistý... Dal jsem to opravit ještě jednomu člověku co učí na vysoké škole a ten mi řekl, že má tvrzení jsou správná, tak teď opravdu nevím :-)
Opravdu si myslíte a stojíte za odpověďmi co jste uvedl?

Marian · 24. 06. 2008 10:56

↑ xy2000:

Stojim si za tim. Pokud jsou nejake nejasnosti nebo nejaka sporna mista, rad prijmu diskuzi. Pokud jsem se v nekterych bodech mylil, pak ukazte ve kterych a uvedte kontrapriklad, popr. dokazte sva tvrzeni.

xy2000 · 24. 06. 2008 11:05

Marian napsal(a):
↑ xy2000:

Stojim si za tim. Pokud jsou nejake nejasnosti nebo nejaka sporna mista, rad prijmu diskuzi. Pokud jsem se v nekterych bodech mylil, pak ukazte ve kterych a uvedte kontrapriklad, popr. dokazte sva tvrzeni.

Tak třeba hned 1. e) to si myslím, že je správně i ve slajdech z přednášek je tam, že druhá derivace rovna nule má v bodě x inflexi.

jelena · 24. 06. 2008 13:29 — Editoval jelena (24. 06. 2008 23:26)

↑ xy2000:

Zdravim :-)

napriklad f(x) = x^4

Jak to ma s inflexi a s 2. derivaci?

↑ Marian:

Zdravim a moc dekuji, ze jsi nasel cas a odpovedel :-)

V tomto tematu mozna vznikne pekna debata :-)

Editace: kdybych tusila, ze kolega ↑ xy2000: nebude argumentovat nazory vlastnimi duvody, samozrejeme, za podpory literatury a dalsich zdroju, ale trochu metodou materske skolky "dovedu starsiho brachu a ten vam ukaze ...", hmm :-(

Marian · 24. 06. 2008 13:51

↑ xy2000:

Holy nesmysl! Celkem by me zajimalo, kdo Vam prednasi a co studujes. Dost by me mrzelo, kdyby nekdo z vyucujicich matematiky na VŠ schvalil, ze 1e je pravda!

Uvedom si, ze nestaci jen "si myslet". Potrebuju k diskuzi padne argumenty a hlavne definice. Neodvolavej se, prosim, na slajdy z prednasky. Kdo vi, kdo je psal, popr. kolik tam je chyb. Ber v uvahu proverene knihy. V cestine treba Jarnikuv Diferencialni pocet I, ze zahranicnich neco od Springeru (mnoho skvelych knih), etc.

Uvedu ti pro jistotu definici inflexniho bodu z Jarnikova Diferencilniho poctu I (NČSAV, Praha 1955):
___________
Inflexni bod. Funkce f(x) necht ma v bode x_0 derivaci. Necht existuje cislo $\delta >0$ tak, ze plati jeden z techto pripadu:
I. Budto lezi bod $[x,f(x)]$ pro $x_0-\delta <x<x_0$ pod tecnou (mysleno ke krivce y=f(x), moje pozn.)
$y=f(x_0)+f'(x_0)\cdot (x-x_0)$
a pro $x_0<x<x_0+\delta$ nad ni.
II. Nebo lezi bod $[x,f(x)]$ pro $x_0-\delta <x<x_0$ nad tecnou
$y=f(x_0)+f'(x_0)\cdot (x-x_0)$
a pro $x_0<x<x_0+\delta$ pod ni.
Pak rikame, ze funkce f(x) ma v bode $[x_0,f(x_0)]$ inflexni bod.
___________

Vemes-li v uvahu napr. funkci f(x)=x^4, mas jasne spor s definici inflexniho bodu (v tomto pripade padalo podezreni na bod x_0=0). Totiz body podezrele z inflexe jsou takove, ze prvni derivace v techto bodech existuje a druha derivace v tomto bode je nulova nebo neexistuje. Zaruku, ze vybrany kandidat je ten spravny, nemas. To se pak da zjistit napr. z chovani znamenka druhe derivace. Ale tyto veci se berou vetsinou i na stredni skole technickeho charakteru nebo na gymnaziich.

Zkus dokazat korektne, ze nemam pravdu. Pak opravim sve reseni v pripade 1e.

Marian · 24. 06. 2008 14:09 — Editoval Marian (24. 06. 2008 15:00)

↑ sneakfast:

Neni pravdou, ze nutna podminka pro existenci inflexniho bodu je nenulovost treti derivace v tomto bode. Existuji funkce, ktere maji druhou derivaci nulovou, treti take (v bode podezrelem z inflexe samozrejme) a presto tam inflexni bod je (ovsem za predpokladu, ze existuje prvni derivace v tomto bode ).

Priklad najdes snadno. Treba f(x)=x^5. Je

f'(x)=5x^4,
f''(x)=20x^3,
f'''(x)=60x^2.

Bod podezrely z inflexe je x_0=0, nebot f''(x)=0 pouze pro x=0. Derivace f'(0) existuje a dale plati f'''(0)=0. Presto tam inflexe je (viz znamenko druhe derivace v okoli bodu x_0=0).

Plati take tato obecna veta (viz treba Jarnik, Diferencialni pocet I):
___________
Věta Necht f(x) je realna funkce a x_0 bod jejiho definicniho oboru. Predpokladejme, ze existuje prirozene cislo n>1 takove, ze 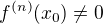$f^{(n)}(x_0)\neq 0$ , ale $f^{(k)}(x_0)=0$ pro 0<k<n. Potom plati
I. Je-li n sude, $f^{(n)}(x_0)>0$ , je funkce f(x) ryze konvexni v bode x_0.
II. Je-li n sude, $f^{(n)}(x_0)<0$ , je funkce f(x) ryze konkavni v bode x_0.
III. Je-li n liche, $f^{(n)}(x_0)>0$ , ma funkce f(x) v bode x_0 inflexi.
IV. Je-li n liche, $f^{(n)}(x_0)<0$ , ma funkce f(x) v bode x_0 inflexi.
___________

Tedy tebou uvedena podminka staci sice na to, aby se jednalo o inflexi, ale nutna neni. Viz priklad vyse a take veta vyse v tomto prispevku.

halogan · 24. 06. 2008 15:27

↑ Marian:

V jakemkoliv tematu, kde se objevujete vy, si nejsem naprosto jisty nicim :) Viz. vcerejsi logaritmy atp.

xy2000 · 24. 06. 2008 15:45

Poslal jsem to dalšímu člověku. Učí matematiku, tak zítra mě dá vědět, jak to má být. A porovnáme výsledky :-)

sneakfast · 24. 06. 2008 16:15

↑ Marian: Je to tak, já si spletl definici inflexního bodu -- hanba mi :)

Nicméně trochu offtopic: zaujala mě Jarníkova definice, která používá slovní spojení "Nech? ...., pak .....", což ve mně vyvolává dojem implikace. Neměly by alespoň formálně být definice ve tvaru ekvivalence? Z Jarníkovy definice není úplně jasné, zda neexistují nějaké body, které jsou inflexní, ač předpoklad neplatí. Nesetkal jsem se s takovým zápisem poprvé :)

Marian · 24. 06. 2008 16:39

↑ sneakfast:

U syntetickych definic je to celkem bezne. Tu definici bych zrejme blize charakterizoval pojmy konstruktivni nebo kontextualni definice.

xy2000 · 25. 06. 2008 09:50

takže výsledky jsou správně a děkuji.
Jen bych se chtěl ještě zeptat ma tohle:

f"(x) + nekonečno --> f není spojitá v bodě x

f má lokální minimum v bodě x --> f´(x)= 0

co je správně ?

jelena · 25. 06. 2008 10:28

↑ xy2000:

Ja bych se primlouvala za posloupnost - zduvodneni - jelikoz ma vlastni limitu.

A smim se zeptat, co bylo duvodem takto radikalni zmeny nazoru na spravnost vysledku?

Tomsus · 25. 06. 2008 11:52

posloupnost sin n/n je omezena, protoze |sin n|<=1 a n ti roste takrikajec "nade vsechny meze", tudiz muzeme udelat odhad:

sin n/n <= |sin n|/n <= 1/n (omlouvam se za neTEXovy zapis)

f''(x) =+oo --> fce nespojita v x neplati --> ted nechci tahat z rukavu fce, o kterych si nejsem jisty, ze to plati, ale da se na to prijit takto: muzeme sestrojit fci f'(x) se skokem v bode a (jinak spojitou), pro kterou plati, ze f''(a)=+oo, to lze - ale jelikoz je f'(x) na nejakem okoli bodu a konecna, tak tam je f(x) spojita (protoze f(x) je na tom okoli diferencovatelna - ma konecnou derivaci)...

pokud ma f lokalni extrem v nejakem bode, pak derivace ani nemusi existovat (prinejmensim lze vytvorit takovou nespojitou fci)

Tomsus · 25. 06. 2008 11:56

↑ sneakfast:

Neumím to tak pěkně pojmenovat jako Marian, ale takových vět je snad i většina. Vždy? zdaleka ne vše jde vyslovit ve tvaru ekvivalence. (např. pokud je funkce diferencovatelná na (a,b), pak je i spojitá na (a,b) --- ale naopak to neplatí a nikdy platit asi nebude).

Marian · 25. 06. 2008 12:11

↑ Tomsus:

↑ sneakfastovi: slo ale o definice, nikoliv o vety nebo lemmata.

Marian · 25. 06. 2008 12:34 — Editoval Marian (25. 06. 2008 13:24)

↑ xy2000:

Jak jiz bylo psano, ani jedno z tech tvrzeni neni obecne pravdive. Ukazu dva velice snadne protipriklady, at to je vice jasne.

1. Budu pracovat s funkci $\frac{3}{4}\cdot\sqrt[3]{x^4}=\frac{3}{4}x^{4/3}$ . Definicni obor teto funkce jsou vsechna relana cisla - to je zrejme, funkce je navic spojita. Prvni a druha derivace ma tvar
$f'(x)=x^{1/3}=\sqrt[3]{x}\qquad\mathrm{a}\qquad f''(x)=\frac{1}{3\cdot\sqrt[3]{x^2}}.$
Je snadno videt, ze plati
$\lim_{x\to 0^+}f''(x)=\lim_{x\to 0^+}\frac{1}{3\cdot\sqrt[3]{x^2}}=+\infty\qquad\mathrm{a}\qquad\lim_{x\to 0^-}f''(x)=\lim_{x\to 0^+}\frac{1}{3\cdot\sqrt[3]{x^2}}=+\infty .$
_______________

2. Vemes funkci f(x)=|x|. Je to funkce dokonce spojita (tak silny predpoklad vubec neni treba, ale jenom lip pro kontrapriklad). Lokalni extrem existuje (snadno z definice funkce |x| a z definice lok. extremu) v bode x=0. Pri derivaci teto funkce uz to bude trochu horsi. Vychazi se z toho, ze pro kladna realna cisla je |x|=x a pro zaporna nebo nulu je |x|=-x. Derivace zleva a zprava v bode x=0 funkce |x| je

$f'_-(0)=-1\qquad\mathrm{a}\qquad f'_+(0)=1.$

Derivace f'(x) v bode x=0 neexistuje, presto je v tomto bode lokalni extrem - totiz ostre lokalni minimum.

Matematické Fórum

#1 23. 06. 2008 14:18 — Editoval xy2000 (23. 06. 2008 14:18)

Která tvrzení jsou správná ?

#2 23. 06. 2008 15:13

Re: Která tvrzení jsou správná ?

#3 23. 06. 2008 19:08

Re: Která tvrzení jsou správná ?

#4 23. 06. 2008 19:41

Re: Která tvrzení jsou správná ?

#5 23. 06. 2008 21:02

Re: Která tvrzení jsou správná ?

#6 23. 06. 2008 21:04 — Editoval sneakfast (23. 06. 2008 21:05)

Re: Která tvrzení jsou správná ?

#7 24. 06. 2008 00:05

Re: Která tvrzení jsou správná ?

#8 24. 06. 2008 01:13 — Editoval Marian (08. 08. 2008 00:37)

Re: Která tvrzení jsou správná ?

#9 24. 06. 2008 08:54

Re: Která tvrzení jsou správná ?

#10 24. 06. 2008 10:42

Re: Která tvrzení jsou správná ?

#11 24. 06. 2008 10:56

Re: Která tvrzení jsou správná ?

#12 24. 06. 2008 11:05

Re: Která tvrzení jsou správná ?

Marian napsal(a):

#13 24. 06. 2008 13:29 — Editoval jelena (24. 06. 2008 23:26)

Re: Která tvrzení jsou správná ?

#14 24. 06. 2008 13:51

Re: Která tvrzení jsou správná ?

#15 24. 06. 2008 14:09 — Editoval Marian (24. 06. 2008 15:00)

Re: Která tvrzení jsou správná ?

#16 24. 06. 2008 15:27

Re: Která tvrzení jsou správná ?

#17 24. 06. 2008 15:45

Re: Která tvrzení jsou správná ?

#18 24. 06. 2008 16:15

Re: Která tvrzení jsou správná ?

#19 24. 06. 2008 16:39

Re: Která tvrzení jsou správná ?

#20 25. 06. 2008 09:50

Re: Která tvrzení jsou správná ?

#21 25. 06. 2008 10:28

Re: Která tvrzení jsou správná ?

#22 25. 06. 2008 11:52

Re: Která tvrzení jsou správná ?

#23 25. 06. 2008 11:56

Re: Která tvrzení jsou správná ?

#24 25. 06. 2008 12:11

Re: Která tvrzení jsou správná ?

#25 25. 06. 2008 12:34 — Editoval Marian (25. 06. 2008 13:24)

Re: Která tvrzení jsou správná ?