Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » objem rotačního tělesa a obsah rotační plochy (TOTO TÉMA JE VYŘEŠENÉ)
#1 02. 07. 2008 19:20
objem rotačního tělesa a obsah rotační plochy
ahoj,
učím se na zkoušku a narazila jsem na tyto dva příklady
1. mám vypočítat objem rotačního tělesa, které vznikne rotací rovinného obrazce ohraničeného osou x a danou křivkou, které je popsaná parametricky + GRAF
x=t^2
y=t-t^3/3 (0,odm3)
2. obsah rotační plochy, která vznikne rotací křivky kolem osy x, zadané parametricky + GRAF
x=e^t*sint
y=e^t*cost (0,pi/2)
Offline
#2 03. 07. 2008 12:46 — Editoval thriller (03. 07. 2008 12:48)
Re: objem rotačního tělesa a obsah rotační plochy
Ahoj, ten první příklad se už tady jednou víceméně počítal: http://forum.matweb.cz/viewtopic.php?id=3618
Jestliže "t" jde od nuly do 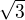 , pak x jde od nuly do trojky. A když si z x=t^2 vyjádřím t a dosadím ho do druhé rovnice, dostanu
, pak x jde od nuly do trojky. A když si z x=t^2 vyjádřím t a dosadím ho do druhé rovnice, dostanu 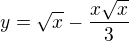 . Teď už lze použít středoškolský vzorec na výpočet objemu
. Teď už lze použít středoškolský vzorec na výpočet objemu 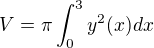 .
.
Tady je obr. zadané křivky
Druhý příklad bych počítal takto. Zapíšu si parametricky rovnici plochy, jejíž obsah mám počítat.
Obr. křivky je zde:
Parametrizace rotační plochy bude  kde pro parametry t a u platí:
kde pro parametry t a u platí:  a
a 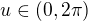
a obsah takové plochy bude 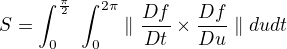 , kde výraz v integrandu se dá vyjádřit také jako odmocnina z determinantu metrického tenzoru, tedy
, kde výraz v integrandu se dá vyjádřit také jako odmocnina z determinantu metrického tenzoru, tedy 
100*0>0 aneb stokrát nic umořilo osla
Offline
#3 06. 07. 2008 11:52
Re: objem rotačního tělesa a obsah rotační plochy
↑ thriller:
Ozývám se znova, když by jsem nemohla použít dvojný integrál. Alespoň s tvého podání to tak vypadá, tak nevím.
Offline
#4 06. 07. 2008 17:25
Re: objem rotačního tělesa a obsah rotační plochy
↑ kiki:
Jestliže nemůžeš v té druhé úloze použít dvojný integrál, tak nevím. Určitě by šlo z parametrického zadání vyjádřit "y" jako funkci "x". Ale nevzpomenu si na žádnej vzorec na výppočet plochy rotačního tělesa. Možná 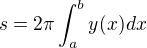 ?
?
100*0>0 aneb stokrát nic umořilo osla
Offline
#5 06. 07. 2008 17:35
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: objem rotačního tělesa a obsah rotační plochy
↑ thriller:
Zdravim :-) ja si tez nepamatuji, ale tady to rikaji, snad dobre :-)
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » objem rotačního tělesa a obsah rotační plochy (TOTO TÉMA JE VYŘEŠENÉ)
