Matematické Fórum

Pavel · 24. 07. 2008 14:13

Najděte reálnou funkci f(x), která je definována na nějakém intervalu <a,b>, je na něm prostá, ale není něm ani na žádném jeho podintervalu monotonní.

kaja.marik · 24. 07. 2008 15:08

může být i nějaká hodně škaredá? (např. v každém bodě nespojitá?)

varianta 2: Najděte požadovanou funkci tak, aby navíc oborem hodnot byla množina reálných čísel.

Pavel · 24. 07. 2008 15:19

může, škaredé bývají nejpěknější (platí jen u funkcí :-) ) Varianta 2 je taky dobrá, tuším řešení.

musixx · 24. 07. 2008 16:15

Napriklad f(x)=x pro x racionalni, f(x)=-x jinak. Prosta je pak zrejme a monotonni neni nikde, protoze na libovolne malem realnem intervalu najdete jak cislo racionalni, tak realne neracionalni.

Marian · 24. 07. 2008 16:20 — Editoval Marian (24. 07. 2008 16:21)

Muj navrh je vzit funkci, nazvu ji treba 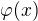$\varphi (x)$ , definovanou na libovolnem intervalu [a,b], a<b, predpisem

$\varphi (x):=x+1-D(x),$
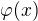kde $D(x):=\chi_{\mathbb{R}}$ je charakteristicka funkce mnoziny realnych cisel - tedy Dirichletova funkce. Funkce $\varphi (x)$ splnuje vsechny podminky uvedene Pavlem.

Jen nevim, jak mam chapat nazev tohoto vlakna, totiz "Prazdninova injekce". Je to injekce matematickeho krasna nebo injektivni zobrazeni?

Marian · 24. 07. 2008 16:28 — Editoval Marian (24. 07. 2008 16:30)

↑ musixx:

Tva funkce se da zapsat jako
$(-1)^{1-D(x)}\cdot x,$
kde D(x) znaci Dirichletovu funkci. Ted jen cekam, s jakou funkci prijde ↑ Pavel:.

Pavel · 24. 07. 2008 20:51

Zkoušel jsem vyřešit 2. variantu, povedlo se jen pro otevřený interval opět s využitím Dirichletovy funkce D(x):

S uzavřeným intervalem mám ale problém.

kaja.marik

↑ Pavel:
jojo, s tím uzavřeným intervalem mám taky problém :(
musí to tam nekde utíkat do nekonečna (aby to byla surjekce na R) a musí tam někde v oboru hodnot zůstat dvě díry, které by se zaplnily dodefinováním funkčních hodnot na krajích....
tezko rict jestli se to povede, taky me reseni pro uzavreny interval nenapada
--------------------------------------------
Kája jen polkl slinu: „Prosím, vzácný pane, jen jestli se to pro mne hodí. To snad jen pro pány, a já budu nejspíš truhlářem.“

Pavel · 24. 07. 2008 21:25

Mám stejnou úvahu. Mám pocit, že přes Dirichleta v kombinaci se známými funkcemi to jen tak jednoduše nepůjde. Uvídíme, co na to Marian :-)

Pavel Brožek · 24. 07. 2008 23:11

Nech? existuje bijekce $f:[a,b]\to\mathbf{R}$ , která neni na žádném podintervalu monotónní. (Tedy vyhovuje zadání varianty 2, jestli jsem dobře pochopil)

Existuje bijekce $\varphi:[a,b]\to[a,b]$ (něco jako přerovnání), že $f\circ\varphi:[a,b]\to\mathbf{R}$ je rostoucí? Pokud ano, pak $f\circ\varphi$ je nutně spojitá (což není těžké ukázat). Vzor otevřené množiny při spojitém zobrazení je otevřená množina, což je spor, protože [a,b] je uzavřená. Zadání by tedy neměla vyhovovat žádná funkce.

Zbývá tedy ukázat, že taková funkce $\varphi$ existuje, aby byla dokázána neexistence řešení. Mě se ji najít nepodařilo, tak snad budete úspěšnější, pokud vůbec existuje.

Pavel · 25. 07. 2008 00:19

Něco mě napadlo, vypadá to zajímavě a až pozoruhodně jednoduše.

Kondr · 25. 07. 2008 03:33

↑ Pavel:Toto zobrazení není prosté, na 0 posílá čísla 0,1,-1.

Jinak stačí použít funkci
$g(x)=tg(x\pi/2)\cdot(-1)^{D(x)}$
a definovat
f(1/n)=g(1/(n+1)) pro všechna přirozená n
f(-1/n)=g(-1/(n+1)) pro všechna přirozená n
f(x)=g(x) pro x různé od 1/n a -1/n pro všechna přirozená n

Pavel · 25. 07. 2008 08:17

Kondr: Vzhledem k tomu, že 1 resp. -1 lze zapsat jako 1/1 resp. 1/-1, je pro ně f(x) definována podle 5. řádku, tedy f(1)=1 resp. f(-1)=-1. Takže f(x) je prostá.

musixx · 25. 07. 2008 11:23 — Editoval musixx (25. 07. 2008 11:26)

Co rikate na tohle reseni varianty 2?

Pisme
$\langle a,b\rangle=A\cup B$
kde
$A=(a,b)\cap(\mathbb R\setminus\mathbb Q)$
$B=\langle a,b\rangle\setminus A$
Tedy A jsou vsechny vnitrni iracionalni body zadaneho intervalu a B jsou vsechny racionalni body zadaneho intervalu plus ty krajni body zadaneho intervalu, ktere nebyly (pripadne) racionalni.

B je spocetna, tedy existuje bijekce $\varphi$ mezi B a $\mathbb Q$ .

Mnozinu A ted zobrazim bijektivne na vsechna iracionalni cisla stejnym procesem, jako se napriklad bijektivne zobrazuje omezeny otevreny interval na cela realna cisla. Tento proces oznacim za funkci 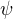$\psi$ . Prevracena hodnota iracionalniho cisla je zrejme opet cislo iracionalni.

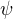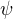Mnoziny A a B jsou zrejme disjunktni. Tedy sjednocenim funkci $\varphi$ a $\psi$ vznikne hledana funkce f, nebot je zrejme prosta a $\varphi$ pokryva vsechna racionalni cisla, zatimco $\psi$ ta iracionalni.

Pavel Brožek · 25. 07. 2008 11:40

↑ musixx:

jak je ale zaručeno, že ta funkce f není na žádném podintervalu monotónní?

musixx · 25. 07. 2008 12:21 — Editoval musixx (25. 07. 2008 12:50)

↑ BrozekP: Ale no tak... :-) Vzdyt ona neni ani spojita, jinak by to byl homeomorfismus, coz mezi uzavrenou (close) a obojetnou (clopen) mnozinou nejde...

Marian · 25. 07. 2008 16:00 — Editoval Marian (25. 07. 2008 16:01)

Vymyslel jsem tuto funkci, prilis slozita mi nepripada, tak jen doufam, ze tam neni nejaka chyba. Hledal jsem funkci f(x), ktera zobrazuje interval [-1,1] na mnozinu vsech realnych cisel, pricemz hledana funkce je prosta a neroste.

Necht $\alpha\in\mathbb{Q}\cap (-1,0)$ a $\beta\in\mathbb{Q}\cap (0,1)$ . Definuji

pricemze D(x) znaci Dirichletovu funkci.

Pavel Brožek · 25. 07. 2008 16:07

↑ Marian:

A jaké jsou funkční hodnoty v $\alpha$ a $\beta$ ?

Marian · 25. 07. 2008 16:11

↑ BrozekP: Uz jsem zjistil taky, ze tam mam dve diry ...

Pokusim se to nejak u/o-pravit. Diky za upozorneni!!!

Pavel Brožek · 25. 07. 2008 16:58

↑ musixx:

není spojitá, ale to neznamená, že není spojitá na žádném podintervalu.

Pavel Brožek · 25. 07. 2008 17:32

Varianta 3:
Najděte spojitou reálnou funkci f(x), která je definována na nějakém intervalu <a,b>, je na něm prostá, ale není na něm ani na žádném jeho podintervalu monotonní.

a varianta 4:
Najděte spojitou reálnou funkci f(x), která je definována na nějakém intervalu <a,b>, ale není na něm ani na žádném jeho podintervalu monotonní.

Marian · 25. 07. 2008 21:55 — Editoval Marian (25. 07. 2008 22:02)

Varianta 2
Trochu bych poopravil to, co jsem napsal v prispevku #17, coz jsem slibil. Jenze jsem nemel hned cas a prijel jsem teprve ted. Proto ta odmlka nekolika hodin.

Funkce f(x) je proste zobrazeni zobrazujici interval [-1,1]; oborem hodnot funkce f(x) je mnozina vsech realnych cisel a neni monotonni na zadnem nedegenerovanem podintervalu intervalu [-1,1].

Pavel · 25. 07. 2008 22:24

Viz varianta 3:

Využil bych faktu, že spojitá funkce zobrazuje uzavřený interval na jednobodovou množinu nebo uzavřený interval. Nech? . Funkce f je prostá, a tak . Bez újmy na obecnosti nech? . Nech? dále .

1. Je-li , pak platí, že a . Odtud plyne, že existuje u takové, že , a tedy
a . V intervalu (x,y) existují alespoň dva body , , , pro které platí , což je spor s injektivitou funkce f.

2. Je-li , je postup obdoný jako v případě 1 a získáváme opět spor s injektivitou funkce f.

3. Aby f byla injektivní, musí tedy platit .

Získáváme tedy závěr, že je-li , pak , což je de facto definice klesající funkce.

Závěr: Má-li být funkce na uzavřeném inervalu spojitá a injektivní, pak nutně musí být monotonní.

Veškeré námitky vítám :-)