Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 23. 11. 2011 21:15 — Editoval mikl3 (23. 11. 2011 21:15)
Re: D(f),H(f) + grafy
↑ Spartak20: do jednoho tématu by měl být jeden příklad
začnu s prvním, je to jednoduché
umíš nakreslit  ? je to parabola se středem
? je to parabola se středem ![kopírovat do textarea $P[0,0]$](/mathtex/9a/9a9c52655759dea8eb047c1f0df30c18.gif) otočená nahoru
otočená nahoru je parabola, která má vrchol a všechny hodnoty posunuté o 1 na ose y, takže vrchol
je parabola, která má vrchol a všechny hodnoty posunuté o 1 na ose y, takže vrchol ![kopírovat do textarea $P[0,1]$](/mathtex/e4/e45adb8e1b7c11208f1fedbacc5dfa09.gif)
 parabola se středem [0,0] otočená dolu
parabola se středem [0,0] otočená dolu parabola otočená dolů posunutá o 1 na ose y výš, vrchol [0,1]
parabola otočená dolů posunutá o 1 na ose y výš, vrchol [0,1]
Offline
#4 23. 11. 2011 21:31
Re: D(f),H(f) + grafy
↑ Spartak20: bavíme se teda o  definiční obor je zřejmě R
definiční obor je zřejmě R
obor hodnot - maxima nabývá tato funkce pro  a to
a to 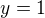 takže hodnotový obor je
takže hodnotový obor je 
Offline
#5 23. 11. 2011 21:31
Re: D(f),H(f) + grafy
↑ Spartak20:
Přesněji 
Ale ano máš to správně.
Pokud jsem Vám pomohl vyřešit příklad, dejte prosím palec :)
Offline
#8 23. 11. 2011 21:47 — Editoval mikl3 (23. 11. 2011 21:49)
Re: D(f),H(f) + grafy
↑ Spartak20:  určíme definiční obor dle odmocniny
určíme definiční obor dle odmocniny to dopočítej
to dopočítej
a pak podle krajní hodnoty urči hodnotový obor
jestli nebudu odpovídat, šel jsem spát
Offline
#10 23. 11. 2011 22:02 — Editoval mikl3 (23. 11. 2011 22:03)
Re: D(f),H(f) + grafy
↑ Spartak20: no bohužel, možná jen překlepy v první části, v druhé chyby
v nerovnici jsi odečítal 7 je to tak? ale na druhé straně je +7
takže vyjde  takže
takže 
nyní za  dosaď krajní bod intervalu tedy
dosaď krajní bod intervalu tedy  a kolik vyjde? a to je minimum hodnotového oboru
a kolik vyjde? a to je minimum hodnotového oboru
ale už jdu spát
Offline
#11 23. 11. 2011 22:11 — Editoval Spartak20 (23. 11. 2011 22:24)
Re: D(f),H(f) + grafy
↑ mikl3:
jo to mi úplně vypadlo, že se přehazují znaménka
takže x=-7/2
napadlo mě udělat si rovnici , takže mi vyšlo že x náleží (+ nekonečno ; -7/2>
a x náleží (-nekonečno ; -7/2>
no ale teď nevím co je co ... mám to jen napsat že d(f) x náleží R a u h(f) je sloučit pomocí U ty hodnoty co mi vyšli ? pokud to takhle nejde (jako že asi ne) , tak mi prosím zítra napiš jak poznám jaká z těch hodnot co mi vyšla je D a jaká H ... Díky
Offline
#12 24. 11. 2011 07:10
Re: D(f),H(f) + grafy
↑ Spartak20: kvůli odmocnině máme podmínku pro definiční obor, to chápeš že? těžko můžeme odmocňovat záporné číslo v reálných číslech, tato podmínka je, že 
pokud definiční obor je omezen (což je), nejsou to všechna reálná čísla, celá osa, pak přeci se nebude jednat o zobrazení všech reálných čísel na reálná (protože jsme některá vyloučili, přesněji interval), ale jen těch přípustných
takže takhle funkce přiřazuje hodnotu číslům z intervalu  podle předpisu
podle předpisu 
nyní hodnotový obor - vysvětlili jsme si, že to nebudou všechna reálná čísla, pochopil jsi proč?
zřejmě tato funkce bude rostoucí a minimum bude mít pro  pak bude nabývat již stále větších hodnot až do nekonečna, zapíšeš to intervalem?
pak bude nabývat již stále větších hodnot až do nekonečna, zapíšeš to intervalem?
Offline
#13 24. 11. 2011 11:31
Re: D(f),H(f) + grafy
↑ mikl3:
podmínka myslím je, že pod odmocninou nesmí být -
a nebudou tam všechna reálná čísla protože je definiční obor omezen -7/2
takže to zapíšu intervalem H(f):y náleží <-7/2;+ nekonečno)
nevím zda to chápu dobře ,ale pokud ano tak se můžeme přesunou na další příklad ,díky
Offline
#15 25. 11. 2011 23:32
- marnes

- Příspěvky: 11227
Re: D(f),H(f) + grafy
↑ Spartak20:
Zkusil bych přes funkci inverzní. Pokud ale budeš chtít postup, tak je to na dlouhé povídání:-(
Jo. A na začátku vás zdravím.
Offline
#17 26. 11. 2011 00:00 — Editoval mikl3 (26. 11. 2011 00:01)
Re: D(f),H(f) + grafy
↑ Spartak20: ten příklad jsme už řešili, definiční obor i hodnotový jsme vyřešili viz ↑ mikl3:
hodnotový se odvíjí podle definičního
ta funkce bude rostoucí a minimum má pro  a to nabývá
a to nabývá  pro všechna
pro všechna  nabývá hodnot
nabývá hodnot  takže
takže  nebo
nebo 
teď už je opravdu pozdě a na řešení těch příkladů 3, 5, 6 se podívám zítra, jestli budu mít čas (spíš ne)
Offline
#18 26. 11. 2011 00:01 — Editoval marnes (26. 11. 2011 00:03)
- marnes

- Příspěvky: 11227
Re: D(f),H(f) + grafy
↑ Spartak20:
Ve stručnosti: určíme Df a Hf, protože u inverzní je to naopak
určíme Df a Hf, protože u inverzní je to naopak
Vyměníme x a y a vyjádříme y ......
...... což je funkce mocninná sudá záporná. Načrtneme její graf - pozor, jen tu část pro její definiční obor, což je obor hodnot zadané
což je funkce mocninná sudá záporná. Načrtneme její graf - pozor, jen tu část pro její definiční obor, což je obor hodnot zadané
Pak znázornit osu prvního a třetího kvadrantu - přímka y=x a potom osově souměrně náš graf zobrazit
Jo. A na začátku vás zdravím.
Offline
#19 26. 11. 2011 00:11
Re: D(f),H(f) + grafy
↑ marnes:
u prvního příkladu mě Váš kolega naučil počítat když je x2 vedle číslice, ale ne když je pod zlomkouvou čarou a jsou tam ještě nějaká jiná čísla ... můžete mi to prosím vysvětlit u toho y=-3/x2 -3 ? to tam stačí místo x2 doplnit tabulkově nějaké číslo a spočítat to ..následně už pak půjde udělat graf ? děkuji
Offline
#20 26. 11. 2011 10:34
- marnes

- Příspěvky: 11227
Re: D(f),H(f) + grafy
 Toto ale není příklad na inverzní funkci. To je jak už bylo psáno funkce kvadratická s rameny směrem dolů,...
Toto ale není příklad na inverzní funkci. To je jak už bylo psáno funkce kvadratická s rameny směrem dolů,...
Můj návod je na funkce, které obsahují odmocninu
Jo. A na začátku vás zdravím.
Offline
#22 26. 11. 2011 10:48
- marnes

- Příspěvky: 11227
Re: D(f),H(f) + grafy
↑ Spartak20:
A co si myslíš že jsem ti napsal v příspěvku číslo 18? Postup po pokročilé? Jiný bohužel nemám, tento nabízím všem studentům.
Jo. A na začátku vás zdravím.
Offline
#24 26. 11. 2011 20:37
- marnes

- Příspěvky: 11227
Re: D(f),H(f) + grafy

Aby jsi věděl, jak vypadá graf této funkce, je potřeba, aby jsi nastudoval mocninné funkce a uměl je posunovat - transformovat. Musíš umět rozlišovat sudé kladné a záporné, liché kladné a záporné.
Pak začneš funkcí 
pak  což je překlopení kolem osy x
což je překlopení kolem osy x
a nakonec  což je posunutí ve směru osy y o 3 díly dolů
což je posunutí ve směru osy y o 3 díly dolů
a tu potom osově souměrně podle přímky 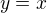
Jo. A na začátku vás zdravím.
Offline

