Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 16. 09. 2008 15:18 — Editoval Marian (16. 09. 2008 16:01)
Re: Súčet radu
↑ lukaszh:
Podle podílového nebo odmocninového limitního kriteria se snadno určí, že daná řada je konvergentní a má tedy smysl ji sčítat. Existuje několik přístupů k součtu této řady. Uvedu postup pouze s jednoduchou manipulací nekonečných řad.
Podle výše uvedeného lze předpokládat, že existuje reálné číslo s takové, že
Toto vynásobíme "kvocientem" 1/2:
Rovnice od sebe odečteme (v pořadí (1)-(2)):
Proto
Offline
#3 16. 09. 2008 15:25 — Editoval ttopi (16. 09. 2008 15:28)
Re: Súčet radu
Pokud chceš součet nekonečné řady (myslím, že je to tak), tak si musíš vyjádřit, jak bude vypadat posloupnost částečných součtů členů řady a z toho pak udělat limitu.
Ta limita by pak měla být součtem řady. Z toho také poznáš, zda řada konverguje či diverguje.
EDIT: Marian už na tom pracuje, tak jsem zvědav na jeho řešení. Snad jsem měl alespoň v něčem pravdu :-)
oo^0 = 1
Offline
#6 16. 09. 2008 15:44
Re: Súčet radu
↑ lukaszh:
Pokud chceš částečné součty, lze k tomu využít metody, kterou jsem prezentoval výše. Navíc Maple 9.5 dává
Indukcí by to jistě šlo celkem dobře dokázat.
Offline
#8 16. 09. 2008 15:57 — Editoval Marian (16. 09. 2008 15:58)
Re: Súčet radu
↑ lukaszh:
Řady typu 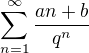 se dají sčítat tímto trikem (samozřejmě za předpokladů o smysluplnosti uvažovaných úprav), přičemž se násobí 1/q a odčítání zůstává.
se dají sčítat tímto trikem (samozřejmě za předpokladů o smysluplnosti uvažovaných úprav), přičemž se násobí 1/q a odčítání zůstává.
Offline
#9 17. 09. 2008 16:05
- Richard Tuček

- Místo: Liberec
- Příspěvky: 1150
- Reputace: 19
- Web
Re: Súčet radu
Já bych zkusil tento trik.
Vyjdu ze známého výsledku:
 je-li
je-li 
Nyní obě strany rovnosti zderivujeme podle a, dostaneme:
tj.  je-li
je-li 
Nyní již není problém dosadit a dopočítat příklad.
Offline

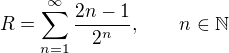


 - hodně šikovné.
- hodně šikovné.