Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 06. 01. 2012 16:18 — Editoval fojjta (06. 01. 2012 16:42)
Vyšetřování množiny bodů
Množina bodů má od bodu ![kopírovat do textarea $A[-6,0]$](/mathtex/b4/b4aa00293abf1c143f2b8eaa4116e1b5.gif) dvakrát větší vzdálenost než od přímky p:
dvakrát větší vzdálenost než od přímky p: .
.
Tedy  .
.
Měli jsme použít způsob, který nás napadne a najít tak tuto množinu, která tvoří kuželosečku.
Díky předchozím zkušenostem mě bylo umožněno použít tento nápad:
Zkusím spočítat libovolné dva body, které v této množině leží. První a nejjednodušší bod bude ![kopírovat do textarea $X_{1}=[-\frac{8}{3},0]$](/mathtex/42/4232b4ba911d2ab9177083613f4ab914.gif) . Pro druhý jsem se rozhodl použít vzorec
. Pro druhý jsem se rozhodl použít vzorec ![kopírovat do textarea $X_{k}=[\frac{x_{a}-\lambda x_{b}}{1-\lambda },\frac{y_{a}-\lambda y_{b}}{1-\lambda }]$](/mathtex/15/1599ed71125263289c53d321f85685ed.gif) kde v tomto případě
kde v tomto případě  . Dále ze zadání víme, že
. Dále ze zadání víme, že  ,
,  a
a  . Tzn. že souřadnice x v bodě
. Tzn. že souřadnice x v bodě  je konstanta
je konstanta  . Z toho jsem vyvodil, že hledanou množinou je přímka v:
. Z toho jsem vyvodil, že hledanou množinou je přímka v:  . Překvapením pro mě bylo, že tento výsledek správný není.
. Překvapením pro mě bylo, že tento výsledek správný není.
V tomto příkladě neprosím o ukázání jiného řešení, teď už ho znám, ale spíše o analýzu mého způsobu, tj. proč je nesprávný.
Offline
#2 06. 01. 2012 16:29
- Hanis

- Veterán

- Místo: Brno
- Příspěvky: 2650
- Škola: PřF MUNI - Statistika a analýza dat
- Pozice: Děvče pro všechno
- Reputace: 148
Re: Vyšetřování množiny bodů
Ahoj, označme hledaný bod X=[x;y]
Jeho vzdálenost od přímky p je tedy 
Vzdálenost tohoto bodu od bodu A je 
A tato vzdálenost má být dvakrát větší:
Stačí upravit.
Offline
#4 07. 01. 2012 17:00
Re: Vyšetřování množiny bodů
Prosím poraďte mi, znovu jsem nad tím několikrát přemýšlel a celý postup se mi stále zdá správný. Jediná nová věc která mě napadla je, že lambda by mohla být také  pro bod mimo úsečku
pro bod mimo úsečku  . Jenže tak bych znovu dostal přímku, tentokrát
. Jenže tak bych znovu dostal přímku, tentokrát  .
.
Offline
#5 09. 01. 2012 00:18
#6 09. 01. 2012 00:39
Re: Vyšetřování množiny bodů
Ahoj,
ve skutečnosti to bude hyperbola, ale na to jsem přišel až ve škole, po mém neúspěšném pokusu. Z mého postupu lze dojít jen k umístění ohnisek a středu hyperboly (pokud na to budu hned pohlížet jako na hyperbolu). Jak jsem psal již dříve, rád bych se dozvěděl chybu v mé úvaze, učebnicové postupy chápu.
Offline
#7 09. 01. 2012 12:45
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Vyšetřování množiny bodů
↑ fojjta:
děkuji, téma jsem našla při procházení nedořešených témat (podle posledního příspívajícího). Postup v úvodním příspěvku neokomentuji, jelikož mu opravdu nerozumím.
Mně se to jako hyperbola nejeví, ale uvažovala jsem jen velmi zběžně. Možna, pokud máš čas a náladu, stalo za to umístit sem správné řešení (ze školy).
Moc jsem nepomohla, tak snad někdo z kolegů. Děkuji.
Offline
#8 09. 01. 2012 12:59
Re: Vyšetřování množiny bodů
POZNAMKA:
"geometricke" problemy je dobre zacat obrazkom
aj geoalgebra existuje... a moze ti dat dobre indikacie
Na zjednodusenie vypoctov v probleme, mozes zmenit suradnicovy system (repère),
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#9 09. 01. 2012 14:47
Re: Vyšetřování množiny bodů
↑ jelena:
Učebnicový/(běžný školní) postup je ten, který už výše předvedl Hanis. Vychází se tam ze vzorce  . Pokud pokračuji ve výpočtu, naleznu rovnici hyperboly:
. Pokud pokračuji ve výpočtu, naleznu rovnici hyperboly:  .
.
I po vykreslení je vidět, že se o hyperbolu jedná:
http://www.wolframalpha.com/input/?i=%2 … 9%5E2+plot
Offline
#11 10. 01. 2012 13:31
Re: Vyšetřování množiny bodů
↑ fojjta:
No já vidím 3 chyby. Jedna je nepodstatná, a to že správně má být ![kopírovat do textarea $X_{1}=\left[-\frac{8}{3},0\right]$](/mathtex/b5/b5c41329a861bcd0530c456eeb9749ab.gif) ,
,
a ta druhá je podstatnější, totiž že vztah ![kopírovat do textarea $X_{k}=\left[\frac{x_{a}-\lambda x_{b}}{1-\lambda },\frac{y_{a}-\lambda y_{b}}{1-\lambda }\right]$](/mathtex/9a/9abaafb1736a4b03abc1ce8f500a53a8.gif) platí pouze pro bod ve vzdálensotí od dvou bodů v daném poměru, s tím že výsledný bod leží na stejné přímce jako dané body. Což zde není splněno.
platí pouze pro bod ve vzdálensotí od dvou bodů v daném poměru, s tím že výsledný bod leží na stejné přímce jako dané body. Což zde není splněno.
Třetí opět nepodstatná chyba je v dosazení -2 za Lambda (neotočení znamínka), což souvisí s první chybou.
Dva jsou tisíckrát jeden.
Offline
#12 10. 01. 2012 22:59
Re: Vyšetřování množiny bodů
↑ Wotton:
Díky za reakci,
1. chybu nechápu, i přes správnou rovnici se to dá ověřit.
ad 2: Jakto, že bod na úsečce/přímce neleží? První bod úsečky je roven vždy A a druhý bod úsečky (pokud hledám body vlevo, tj. mezi body  ) bude ležet na přímce p. Tedy mám i x-ovou souřadnici druhého bodu úsečky a poměr udávající kde bude X na úsečce ležet. Pokud budu chtět hledat body na pravé straně, použiji
) bude ležet na přímce p. Tedy mám i x-ovou souřadnici druhého bodu úsečky a poměr udávající kde bude X na úsečce ležet. Pokud budu chtět hledat body na pravé straně, použiji  a stejné známé body.
a stejné známé body.
ad 3: také nechápu, použít lze přeci jak zápornou tak kladnou hodnotu, viz ad 2
Prosím o vysvětlení, díky.
Offline
#13 11. 01. 2012 00:45 — Editoval vanok (11. 01. 2012 00:46)
Re: Vyšetřování množiny bodů
↑ vanok:,
Pokracujem v mojej poznamke, specialne pre amaterov transformacie suradnicoveho afineho systemu (repère affine)
Poznamka: ak najprv skusime riesit probleme na realnej osy
mame takuto konfiguraciu:
.... ...........
...........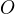 ....
.... ...
...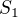 .....
..... .......
.......
kde  je dany bod;
je dany bod;  bod danej priamky (taky ze
bod danej priamky (taky ze  z danou priamkou)
z danou priamkou) 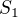 ,
,  riesenie problemu na nasej osy
riesenie problemu na nasej osy
A konecne 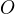 stred
stred ![kopírovat do textarea $[S_1S_2]$](/mathtex/a1/a150713e7f41cfabab6ff3233d26fa25.gif) , ktory vyberieme za pociatok suradnic.
, ktory vyberieme za pociatok suradnic.
Cize na tejto afinej osy mame suradnice 
Toto nas prirodzene vedie k afinemu suradnicovemu ortonormalnemu systemu z pociatkom 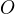 a osou x predoslu os na ktorej som riesil zjednoduseny problem.
a osou x predoslu os na ktorej som riesil zjednoduseny problem.
A co je mimoriadne zaujimave ze v tomto afinom systeme suradnic riesenie sa najde vo velmi jednoduchej forme....a aby sme mali rovnicu v povodnom systeme, staci urobit jednu translaciu a rotaciu .
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#14 11. 01. 2012 10:23
Re: Vyšetřování množiny bodů
↑ fojjta:
K první chybě, ... bohužel jsem to zapomněl opravit, má to být ![kopírovat do textarea $X_{1}=\left[-\frac{4}{3},0\right]$](/mathtex/49/496f4a65a94f7bdce95958b9d597bbdf.gif) . Každopádně, není pravda, že
. Každopádně, není pravda, že 
Ke třetí chybě. Sice je pravda, že bys moh použít  pak bys byl ale na druhé straně přímky. Problém ale je v tom, že jsi v čitateli zlomku znaménko neotočil a ve jmenovateli otočil. Takže jsi vlasntě nepoužil ano jedno.
pak bys byl ale na druhé straně přímky. Problém ale je v tom, že jsi v čitateli zlomku znaménko neotočil a ve jmenovateli otočil. Takže jsi vlasntě nepoužil ano jedno.
No a teď to zásadní. Tak jak to děláš, to je vlastně tak, že vezměš (libovolný) bod na přímce p a bod A a najdeš bod který leží na jejich spojnici ve správném poměru. Tímto postupem opravdu získáš přímku (přesněji 2 přímky. Jednu pro lambda kladné a druhou pro záporné). Jenže vzdálenost od přímky p se přece určuje jinak!
Tak snad už to trklo, ... kdyžtak zas něco připíšu.
Dva jsou tisíckrát jeden.
Offline
#15 11. 01. 2012 11:06 — Editoval Rumburak (11. 01. 2012 11:09)
Re: Vyšetřování množiny bodů
Ahoj.
Zadání podané v ↑ fojjta:
fojjta napsal(a):
Množina bodů má od bodu
dvakrát větší vzdálenost než od přímky p:
..[/b]
nevede k jednoznačnému výsledku .
Dalším řešením je např. kružnice (tedy rovněž kuželosečka) o středu [-3, 0] a poloměru 1 , jejíž vzdálenost od bodu A je 2
a od dané přímky 1 .
Připadá mi, že kružnic v polorovině x < -1 řešících tuto úlohu by se dalo nalézt nekonočně mnoho. (Kde budou ležet jejich středy ?)
Nebo jsem zadání pochopil blbě ?
Offline
#16 11. 01. 2012 11:15
Re: Vyšetřování množiny bodů
↑ Rumburak:
Ahoj
Obávám se že ano, že jsi to pochopil blbě, .... tedy příliš doslova.
Asi by bylo lepší to formulovat takhle:
fojjta napsal(a):
Nalezněte množinu bodů jež mají od bodu
dvakrát větší vzdálenost než od přímky p:
.
Dva jsou tisíckrát jeden.
Offline
#18 11. 01. 2012 13:56
Re: Vyšetřování množiny bodů
Ahoj ↑ Rumburak:,
Staci riesit analyticky v v jednoduchom "repère" ↑ vanok:, ktory som popisal tu a lahko najdes kompletne riersenie problemu.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#20 13. 01. 2012 16:53
Re: Vyšetřování množiny bodů
↑ vanok:
Ahoj kolego,
bohužel hned na začátku Tvé úvahy
vanok napsal(a):
mame takuto konfiguraciu:
...............
....
...
.....
.......
kdeje dany bod;
bod danej priamky (taky ze
z danou priamkou)
,
riesenie problemu na nasej osy
A konecnestred
, ktory vyberieme za pociatok suradnic.
Cize na tejto afinej osy mame suradnice
se ztrácím:
Co jsou ony body (?) "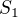 ,
,  riesenie problemu na nasej osy" ? Kterou osu zde máš na mysli ? A kterou úlohu řešíš ? Hledáš
riesenie problemu na nasej osy" ? Kterou osu zde máš na mysli ? A kterou úlohu řešíš ? Hledáš
množinu, která má od bodu A dvojnásobnou vzdálenost než od přímky p,
jak napsal autor tématu, nebo
množinu, které mají od bodu A dvojnásobnou vzdálenost než od přímky p ?
jak se to nakonec "zvrtlo" ?
Offline
#21 13. 01. 2012 18:21
Re: Vyšetřování množiny bodů
↑ Rumburak:
Dakujem, ze sa zaujimas o ine ako vraj oficialne riesenia ( i ked su pre ziakov urcite casto nepochopitelne) .
Odpoved na tvoje male otazky
Os co som vybral je kolma na danu priamku ... ( a osa symetrie ...hladaneho geometrickeho miesta bodov ... )
Ako vidim sa ti to tazko cita...( asi dovod toho ze v CZ a SK nepoznam ich terminologiu ...a sa vyjadrovat popisne je unavne )
Bod D je vlastne "stopa" z priamky ...
Vsak jednoducha analyza problemu ti da prirodzene moj vyber suradnicoveho systemu.
A ak si pozorne cital co pisem riesim ulohu ako chcel autor textu.
MYSLIENKA JE ZE PRACA V NEVHODNOM "REPERE" DA ZBYTOCNU ROBOTU
A V MOJOM "REPERE" SA ULOHA RIESI ZA 3, 4 MINITY MAXIMALNE.... a potom transformacie "REPEROv" sa ucia uz tri roky pred maturitou tak nevidim preco by sa nemali pouzivat.
Ale cestu k rieseniu aku si niekdo vyberie to nie je moja vec.
Inac kde sa najde po CZ, SK nejaka ebook, alebo online o AFINEJ GEOMETRII ( co urcuje pouzivanu terminologiu)...
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#22 13. 01. 2012 22:13
Re: Vyšetřování množiny bodů
↑ vanok:
Děkuji za vysvětlení.
Geometrii bohužel pořádně neumím , ani pokud jde o terminogii. Nedavno jsem narazil na NETu na nějaká česká skripta
(snad stavební fakulty ?) pojednávající o afinní geometri a připadala mi celkem slušně napsaná - třeba je také najdeš.
Myslím, že jsem tehdy hledal heslo "konvexní obal" .
Offline
#23 14. 01. 2012 00:05
Re: Vyšetřování množiny bodů
↑ Rumburak:,
To ma ani velmi neprekvapuje... ked som bol este v CS, tak uz vtedy geometria bola ako ubohe dieta matematiky...
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline