Matematické Fórum

Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.

Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.

Nejste přihlášen(a). Přihlásit

Stránky: 1

 

#1 07. 01. 2012 19:13

divnypatron
Zelenáč
Příspěvky: 1
Reputace:   0 
 

Integrál odmocniny

Nevěděl by někdo?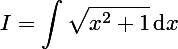

http://forum.matweb.cz/upload3/img/2012-01/59927_mathtex.cgi.gif

Snažil jsem se to všemožně substituovat ale prostě nevím.

Offline

 

#2 07. 01. 2012 19:22 — Editoval jarrro (07. 01. 2012 19:23)

jarrro
Příspěvky: 5472
Škola: UMB BB Matematická analýza
Reputace:   303 
Web
 

Re: Integrál odmocniny

$x^2+1=t^2\nl 2x\mathrm{d}x=2t\mathrm{d}t\nl \sqrt{x^2+1}\mathrm{d}x= \frac{x\sqrt{x^2+1}}{x}\mathrm{d}x=\frac{t^2}{\sqrt{t^2-1}}\mathrm{d}t$

MATH IS THE BEST!!!

Offline

 

#3 07. 01. 2012 19:26 — Editoval vanok (07. 01. 2012 19:32)

vanok
Příspěvky: 14540
Reputace:   742 
 

Re: Integrál odmocniny

Ahoj ↑ divnypatron:,
Divne, ty nevies pozdravit?
NApadaju mi dve metody:
1) pouzit sh, ak poznas hyperbolicke funkcie
2) per partes
$f(x)=\sqrt{x^2+1}$, $df=...$
$dg=dx$=>$g=...$
kde pouzijes ako druhu etapu toto:
derivuj
$\log |x+\sqrt{x^2+1}| + K $ a pouzi po integracii per partes

Staci?

Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT

Offline

 

#4 07. 01. 2012 20:17

jelena
Jelena
Místo: Opava
Příspěvky: 30020
Škola: MITHT (abs. 1986)
Pozice: plním požadavky ostatních
Reputace:   100 
 

Re: Integrál odmocniny

Zdravím v tématu :-)

to je náš zlatý fond (i s náhledem na str. sbírky Hlaváčka).

↑ vanok:

jak jste na Západě na tom s metodou Остроградского (ve francouzských směrech by měl být velmi znám)? - příspěvek 9 v odkazu. Děkuji.

Offline

 

#5 07. 01. 2012 20:34 — Editoval vanok (07. 01. 2012 20:49)

vanok
Příspěvky: 14540
Reputace:   742 
 

Re: Integrál odmocniny

Ahoj ↑ jelena:,
Dakujem za to upozornenie...( co vidim ako zabavne vratenie mojej poznamky) nevedel som ze Ostrogradski systematizoval teoriu neurcitych integralov...
Ale je to dobry  pedagogocky pristup, najma pre nematematikov... za podmienky ze vedia porovnavat koeficienty.... a co je mimoriadne, ze prace z 19° storocia su  stale aktualne...
Inac z ruskych prac matematikov mam rad Cebyseovu ( to je dobra transkripcia?)  teoremu o ekvioscilacii ( idem to hned dat do peknych teorem!)

Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT

Offline

 

#6 07. 01. 2012 20:45

jelena
Jelena
Místo: Opava
Příspěvky: 30020
Škola: MITHT (abs. 1986)
Pozice: plním požadavky ostatních
Reputace:   100 
 

Re: Integrál odmocniny

↑ vanok:

děkuji, Остроградский - pro svou povahu je považován za takovou bájnou postavu, hodně historek. Jinak zde je těžko najít téma, které se ještě nediskutovalo - transkripce a výslovnost :-)

Offline

 

#7 07. 01. 2012 20:52

vanok
Příspěvky: 14540
Reputace:   742 
 

Re: Integrál odmocniny

↑ jelena:,
Dobre, opravil som ako som mohol bez diakritily to meno Cebysev.... no dufam ze mi  nikto nebude vycitat tu moju ubohu transkripciu.... a dal som, ako som slubil, jednu jeho teoremu do "PEKNYCH TEOREM"

Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT

Offline

 

 

Stránky: 1

Zápatí

Powered by PunBB
© Copyright 2002–2005 Rickard Andersson